A system consists of two identical cubes, each of mass m, linked together by the compressed weightless spring of stiffness ϰ (figure). The cubes are also connected by a thread which is burned through at a certain moment. Find:
(a) at what values of Δl, the initial compression of the spring, the lower cube will bounce up after the thread has been burned through:
(b) to what height h the centre of gravity of this system will rise if the initial compression of the spring Δl=7mg/ϰ.
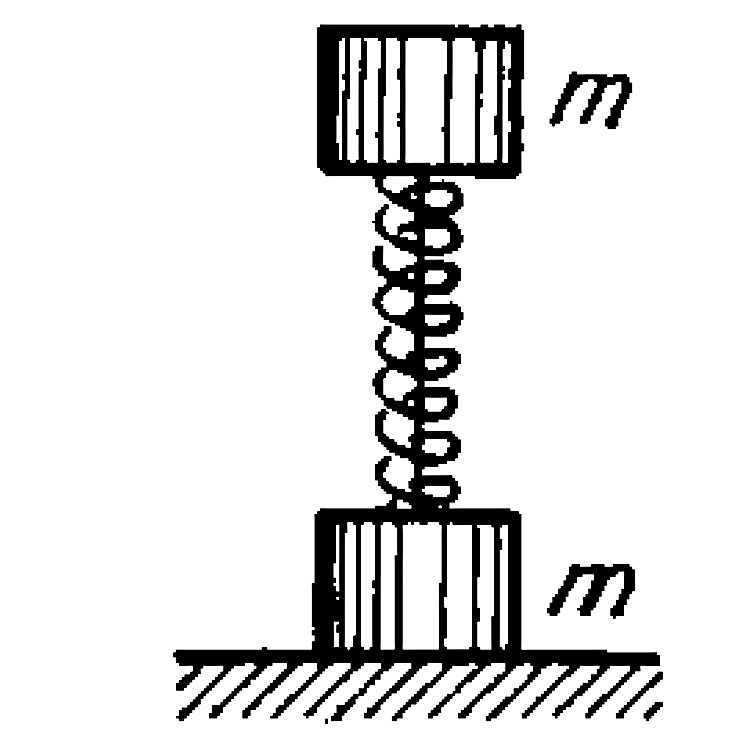
(a) The initial compression in the spring Δl must be such that after buring of the thread, the upper cube rises to a height that produces a tension in the spring that is atleast equal to the weight of the lower cube. Actually, the spring will first go from its compressed state to its natural length and then get elongated beyond this natural length. Let l bet the maximum elongation produced under these circumstances.
Then kl=mg (1)
Now, from energy conservation,
12kΔl2=mg(Δl+l)+12kl2 (2)
(Because at maximum elongation of the spring, the speed of upper cube becomes zero)
From (1) and (2),
Δl2−2mgΔlk−3m2g2k2=0 or, Δl=3mgk, −mgk
Therefore, acceptable solution of Δl equals 3mgk
(b) Let v the velocity of upper cube at the position (say, at C) when the lower block breaks off the floor, then from energy conservation.
12mv2=12k(Δl2−l2)−mg(l+Δl)
(where l=mg/k and Δl=7mgk)
or, v2=32mg2k (2)
At the position C, the velocity of C.M, vC=mv+02m=v2-Let, the C.M. of the system (spring+ two cubes) further rises up to Δyc2.
Now, from energy conservation,
12(2m)v2C=(2m)gΔrC2
or, ΔyC2=v2C2g=v28g=4mgk
But, uptil position C, the C.M. of the system has already elevated by,
ΔyC1=(Δl+l)m+02m=4mgk
Hence, the net displacement of the C.M. of the system, in upward direction
ΔyC=ΔyC1+ΔyC2=8mgk

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A system consists of two identical blocks, each of mass m, linked together by the compressed weightless spring of stiffness k, as shown in figure -3.57. The blocks are connected by a thread which is burned through at a certain moment. Find
(a) At what values of initial compression, the inital compression of the spring, the lower block will bounce up after the thread has been burned through
To what height will the centre of gravity of this system will rise if the initial compression of the spring is 7 mg/k

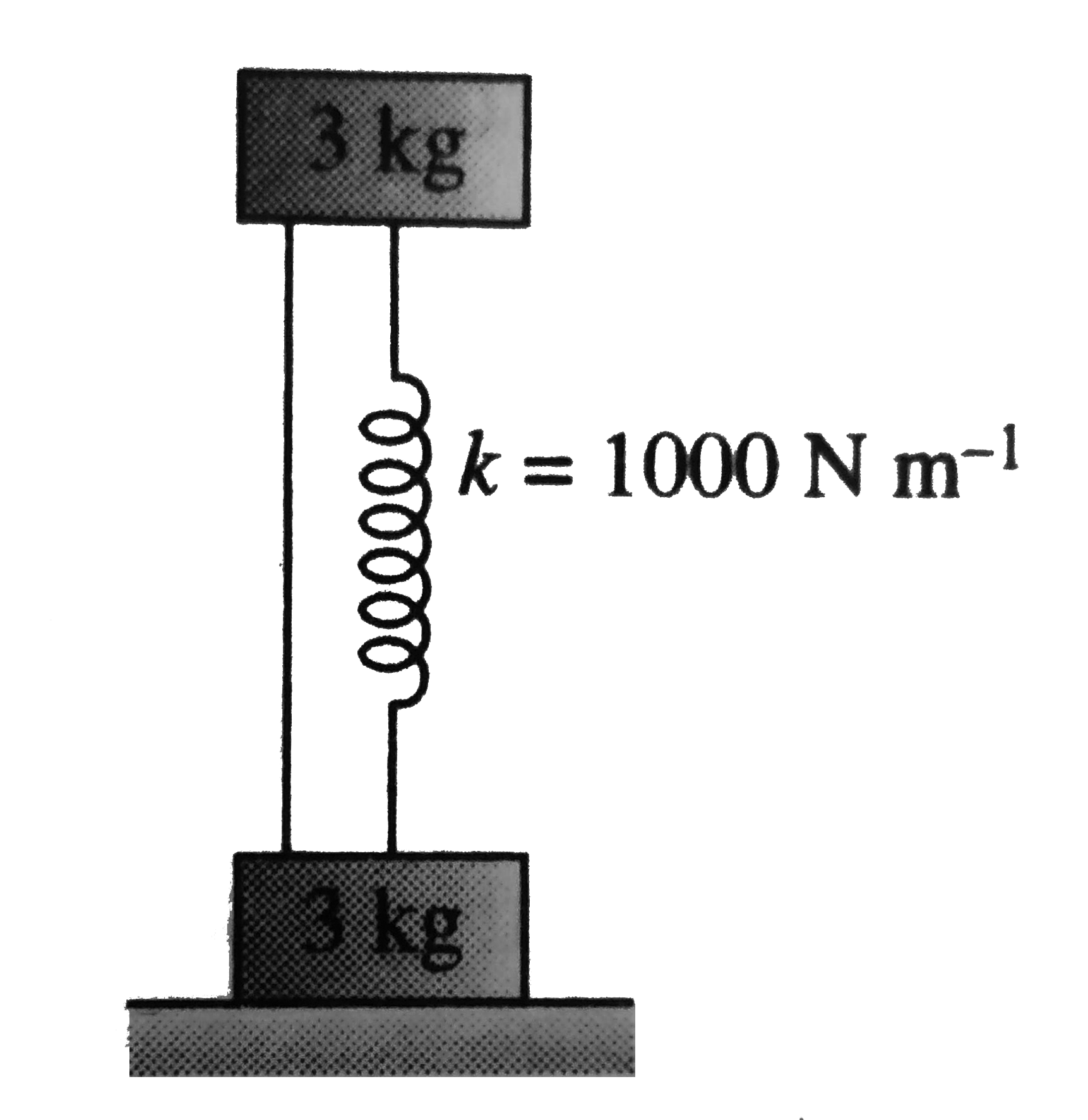
View SolutionA system consists of two identical cubes, each of mass 3kg, linked together by a compressed weightless spring of force constant 1000Nm−1. The cubes are also connected by a thread which is burnt at a certain moment. At what minimum value of initial compression x0 (in cm) of the spring will the lower cube bounce up after the thread is burnt together?
View Solution
Knowledge Check
Find maximum compression is the spring from the given figure.
 A√25mB16√25mC3√25mD6√25m
A√25mB16√25mC3√25mD6√25mA system consists of two cubes of mass m1, and m2 respectively connected by a spring of force constant k. force (F) that should be applied to the upper cube for which the lower one just lifts after the force is removed, is
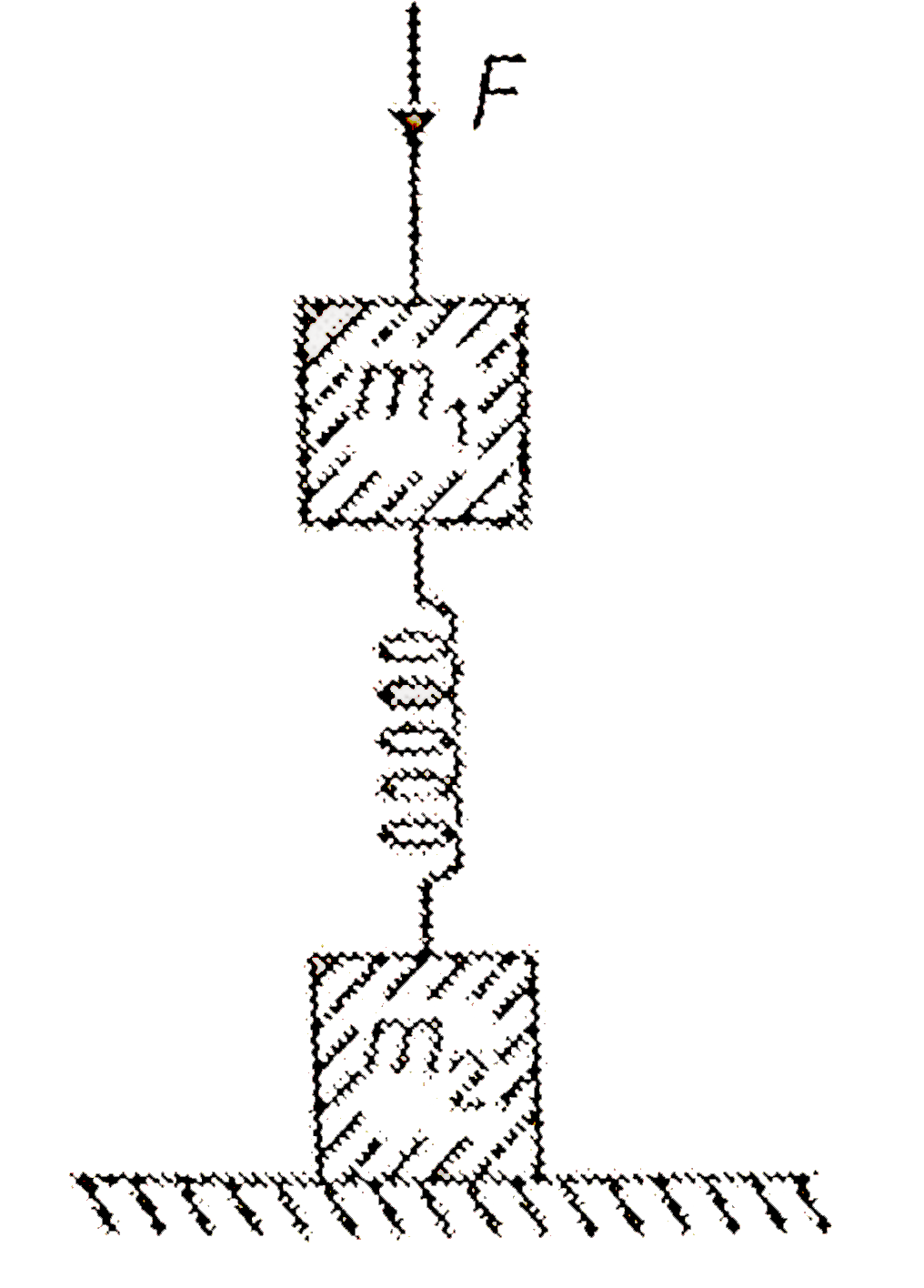 AmgBm2gC(m1+m2)gDm1m2m1+m2g
AmgBm2gC(m1+m2)gDm1m2m1+m2g
Two blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionTwo cubes of mass m1 and m2 are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.

View SolutionTwo identical blocks, each of mass m, are connected through a massless spring of force constant k and arranged as shown in fig the spring is compressed by an amount y by applying an external force and released
(a) What is the velocity of upper block when the spring is relaxed
(b) What should be the initial compression of the spring so that the lower block is just raised above the floor ?

View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness ϰ (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
View SolutionTwo identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View Solution

