Two interacting particles from a closed system whose centre of inertia is at rest. Figure illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass m2. Draw the trajectory of the particle of mass m2 if m2=m1/2.

As the closed system consisting two particles m1 and of m2 is initially at rest the C.M. of the sytem will remain at rest. Further as m2=m1/2, the C.M. of the sytem divides the line joining m1 and m2 at the moments of time in the ratio 1:2. In addition to it the total linear momentum of the system at all the times is zero. So →p1=−→p2 and therefore the velocities of m1 and m2 are also directed in opposite sense. Bearing in mind all these thing, the sought trajectory is as shown in the figure.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Calculate the position of centre of mass of a system consisting of two particles of masses m_1 and m_2 separated by a distance L apar, from m_1?
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View Solution
Knowledge Check
Two interacting particles form a closed system whose centre of mass is at rest. Fig. illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass m1. Select the trajectory of the particle of mass m2 if m2=m1.
 A
A B
B C
C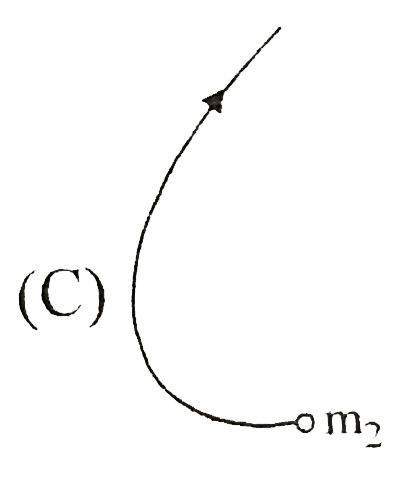 D
D
A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
A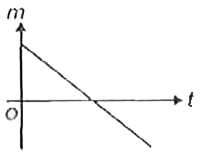 B
B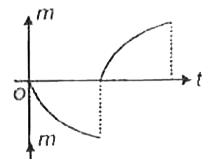 C
C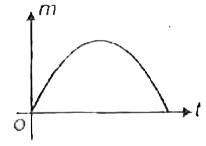 D
D
The reduce mass of two particles having masses m and 2 m is
A2 mB3 mC2 m/3Dm/2
A particle is moving in a circle of radius 2 m. Show the following position of the particle.
2 m from the centre towards south.
View SolutionA particle (A) of mass m1 elastically collides with another stationary particle (B) of mass m2. Then :
View SolutionThe position of centre of mass of a system consisting of two particles of masses m1 and m2 seperated by a distance L apart , from m1 will be :
View SolutionIf →RCM is the position of the centre of mass of a system of two particles of masses m1 and m2 then →RCM is given by :
View SolutionA system consits of n identical particles each of mass m. The total number of interactions between particles possible are :
View Solution

