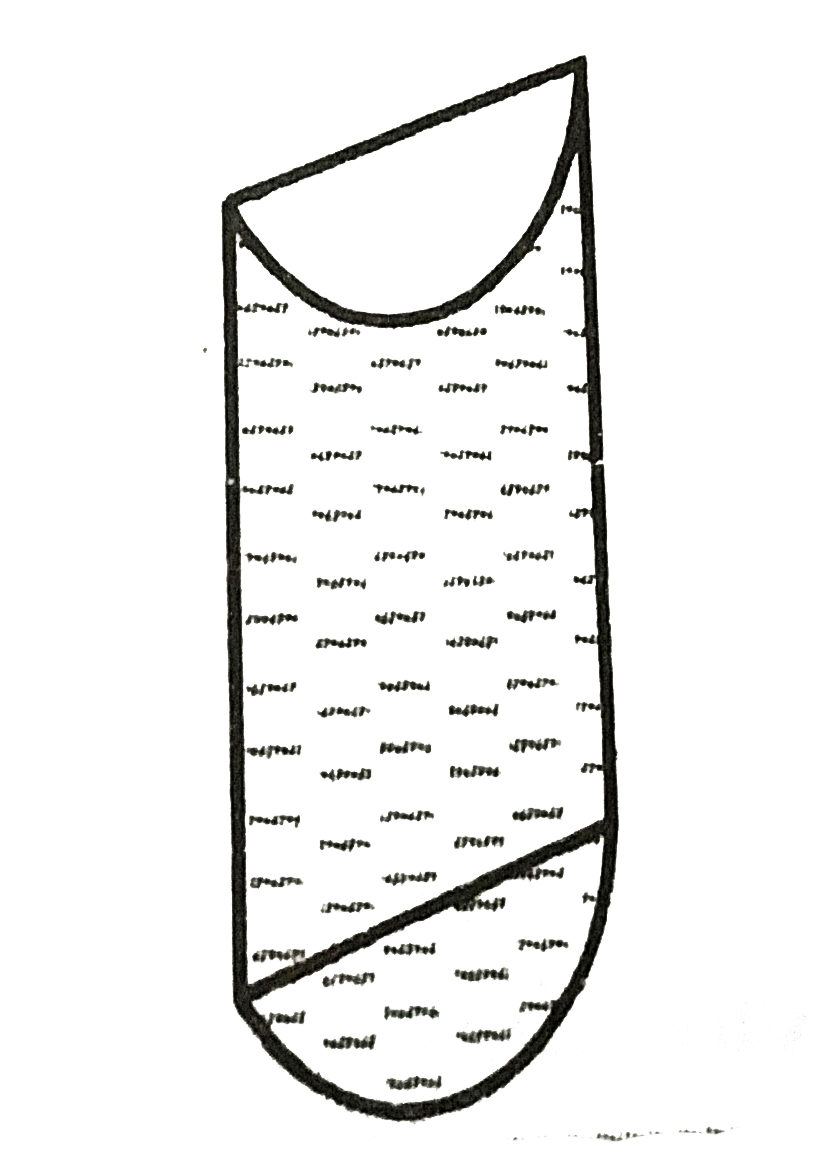
A liquid is contained in a vertical tube of semi-circular cross-section. The angle of contact is zero fig. What is the ratio of the force of surface tension on the curved part and the flat part of the tube?

A

$2 : π$

B

$1 : π$

C

$3 : π$

D

$2.7 : π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Effective length of flat part = 2r
Effective length of curved part is $π r$
So, required ratio is $2 : π$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A liquid is filled into a semi eliiptical cross section with a as semi major axis and b as semi minor axis. The rato of surface tension forces on the curved part and the plane part of the tube in vertical position will be
A $\frac{π (a + b)}{4 b}$
B $\frac{2 π a}{b}$
C $\frac{π a}{4 b}$
D $\frac{π (a - b)}{4 b}$
Question 2 - Select One
A liquid is coming out from a vertical tube. The relation between the weight of the drop W , surface tension of the liquid T and radius of the tube r is given by, if the angle of contact is zero
A $W = π r^{2} T$
B $W = 2 π r T$
C $W = 2 r^{2} π T$
D $W = \frac{3}{4} π r^{3} T$
Question 3 - Select One
A liquid of density $ρ$ and surface tension $σ$ rises in a capillary tube of inner raduis R. The angle of contact between the liquid and the glass is $θ$ . The point A lies just below the maniscus in the tube and the point B lies at the outside level of liquid in the beaker as shown in figure. The pressure at A is

A $p_{B} - ρ g h$
B $p_{B} - \frac{2 σ cos θ}{R}$
C $p_{a t m} - \frac{2 σ cos θ}{R}$
DAll of these

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.58

Home
Ask Doubt
Profile