A spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
μ2m2g22k
2μm2g2k
μ2m2g2k
3μ2mg2k
The correct Answer is:A
To solve the problem of determining the potential energy stored in a spring compressed by a block on a rough surface, we can follow these steps:
Step 1: Understand the Forces Involved
When the block of mass m compresses the spring, it experiences two main forces: the spring force Fs acting to restore the spring to its equilibrium position and the frictional force Ff opposing the motion of the block. The maximum static friction force can be expressed as:
Ff=μN
where μ is the coefficient of friction and N is the normal force. For a horizontal surface, the normal force N is equal to the weight of the block, which is mg. Thus, we have:
Ff=μmg
Step 2: Relate Spring Force to Friction
The spring force can be expressed using Hooke's Law as:
Fs=kx
where k is the spring constant and x is the compression of the spring. For the block to remain at rest while compressing the spring, the spring force must equal the maximum friction force:
kx=μmg
Step 3: Solve for Compression x
From the equation kx=μmg, we can solve for x:
x=μmgk
Step 4: Calculate the Potential Energy Stored in the Spring
The potential energy U stored in a compressed spring is given by the formula:
U=12kx2
Substituting the expression for x we found in Step 3:
U=12k(μmgk)2
Simplifying this expression:
U=12k⋅μ2m2g2k2=μ2m2g22k
Final Answer
Thus, the potential energy stored in the spring when compressed by the block is:
U=μ2m2g22k
---
When the block of mass m compresses the spring, it experiences two main forces: the spring force Fs acting to restore the spring to its equilibrium position and the frictional force Ff opposing the motion of the block. The maximum static friction force can be expressed as:
Ff=μN
where μ is the coefficient of friction and N is the normal force. For a horizontal surface, the normal force N is equal to the weight of the block, which is mg. Thus, we have:
Ff=μmg
The spring force can be expressed using Hooke's Law as:
Fs=kx
where k is the spring constant and x is the compression of the spring. For the block to remain at rest while compressing the spring, the spring force must equal the maximum friction force:
kx=μmg
From the equation kx=μmg, we can solve for x:
x=μmgk
The potential energy U stored in a compressed spring is given by the formula:
U=12kx2
Substituting the expression for x we found in Step 3:
U=12k(μmgk)2
Simplifying this expression:
U=12k⋅μ2m2g2k2=μ2m2g22k
Thus, the potential energy stored in the spring when compressed by the block is:
U=μ2m2g22k
Similar Questions
A block of mass m is pulled by a constant power P placed on a rough horizontal plane. The coeficient of friction between the block and surface is μ. Find the maximum velocity of the block.
View SolutionTwo blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View Solution
Knowledge Check
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreasesFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
If the coefficient of friction between the block and wedge is μ, and the block comes to rest with respect to wedge at a point E on the rough surface then BE will beAHμBH−hμChμDnone of theseA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNone
A block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
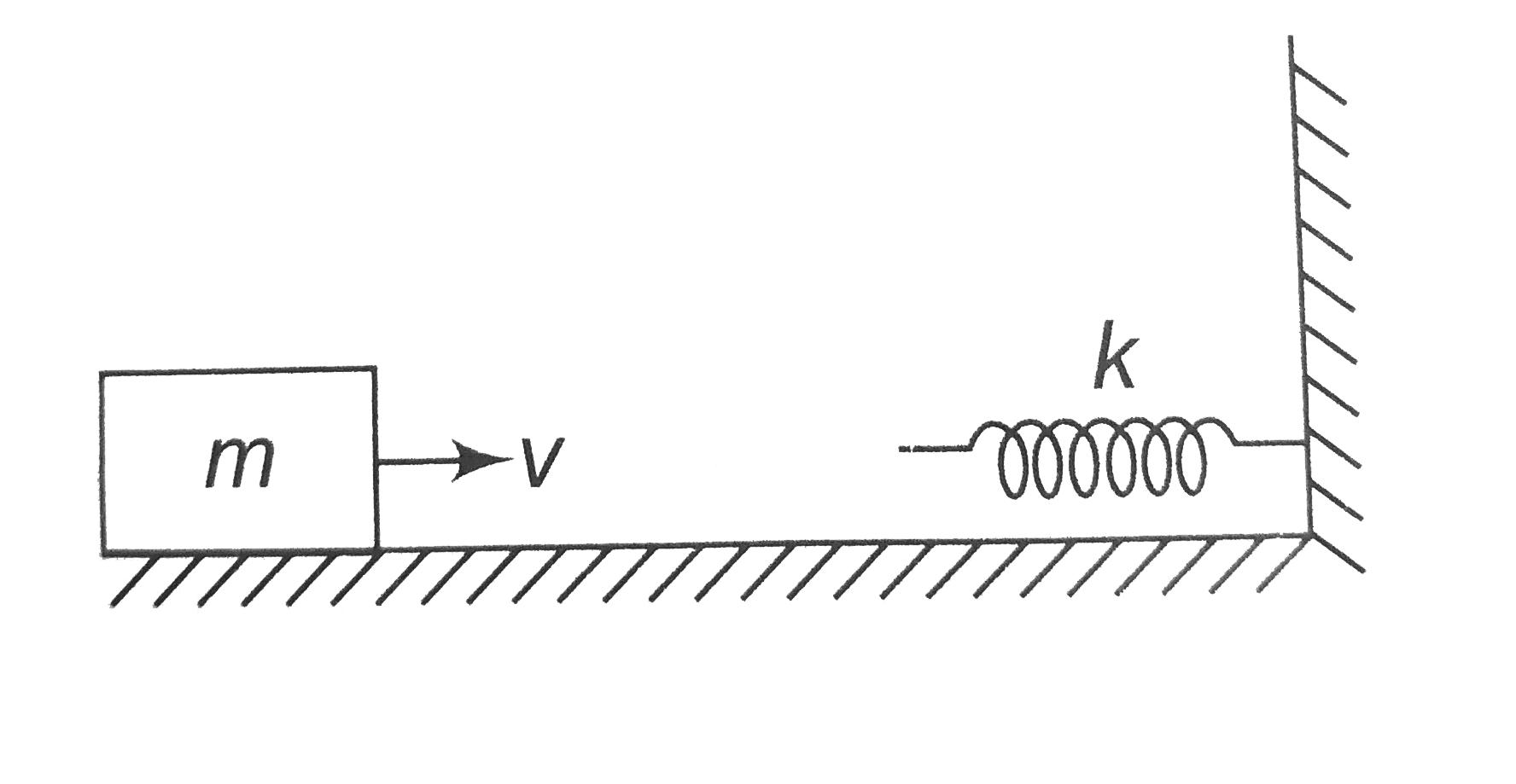
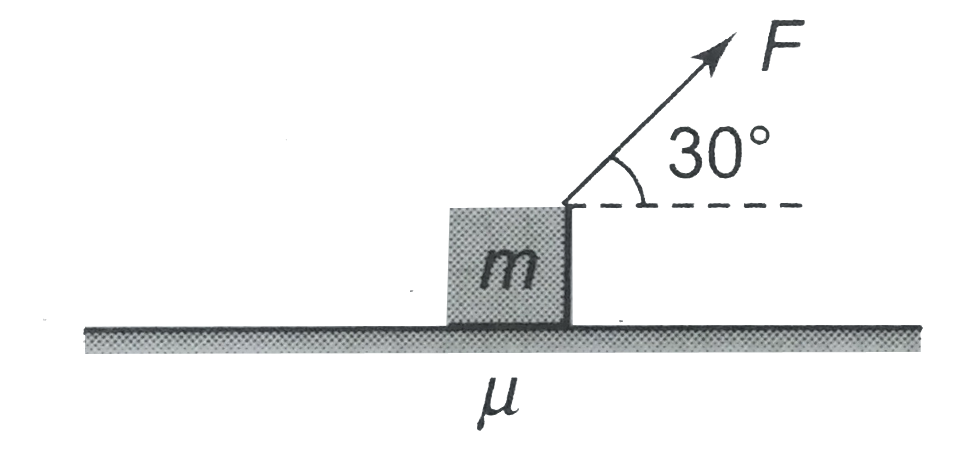
View SolutionA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
View SolutionTwo blocks each of mass m are joined together using an ideal spring of force constant K and natural length l0 . The blocks are touching each other when the system is released from rest on a rough horizontal surface. Both the blocks come to rest simultaneously when the extension in the spring is l04. The coefficient of friction between each block and the surface (assuming it to be same between any of the blocks and the surface) is :
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution

