A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is

−μmgk+1k√(μmg)2+mkv2
μmgk+1k√(μmg)2+mkv2
−μmgk+1k√(μmg)2−mkv2
μmgk+1k√(μmg)2+mkv2
The correct Answer is:A
In pressent of friction both the spring force and the frictional act so as to oppose the compression of the spring
Work done by the net force
W=−12kx2m−μmhsm
where xm is the maximum compression of the spring change in kinetic energy
ΔK=K1−K1=0−12mv2
Accerding to worik energy therem
W=ΔK
−12kx2m−μmgxm=−12mv2
kx2m+μmgxm=12mv2
kx2m+2μmgxm=−mv2=0
x2m+2μmgxmk−mv2k=0
it is a quadratic equation in xm
Solving this equation for xm is positive we get
xm=−μmgk+1k√(μmg)2+mkv2
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Potential Energy, Conservative And Non-Conservative Forces
Explore 28 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Conservation Of Mechanical Energy And Linear Momentum
Explore 24 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Chapter Test
Explore 29 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A block of mass m moving at a speed v compresses as spring thrugh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
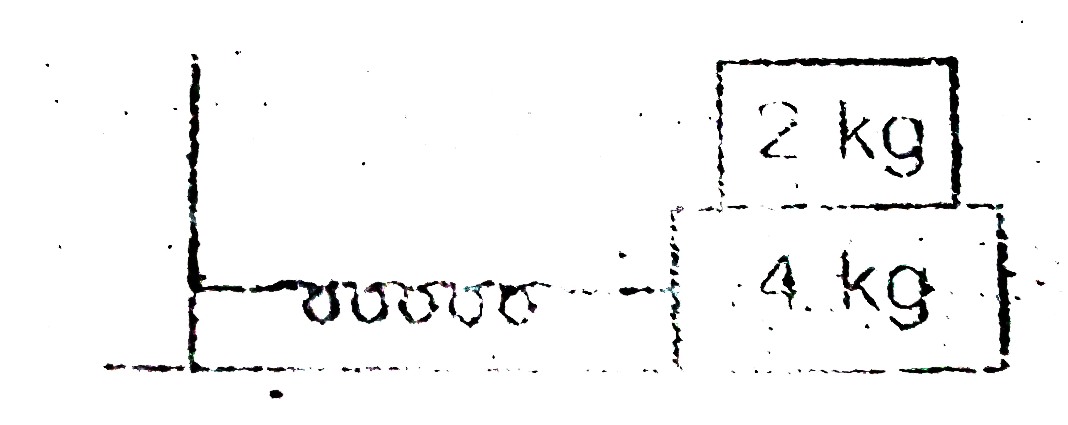
View Solution
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be
 A0.5 mB0.15 mC1.5 mD0.12 m
A0.5 mB0.15 mC1.5 mD0.12 mA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
mass of 0.5 kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be
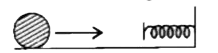
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View Solution

