A rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be

π√m3k
3π2√m3k
π[√m3k+√3g2L]
3π2[√m3k+4√3g2L]
When rod moves right word to the line AB
τA=kLθLcosθ+12k(L2)θ(L/2)cosθ
Hence, θ→0⇒cosθ=1
τA=[4kL2+12kL24]θ⇒mL23α=(4k+12k)L24θ
⇒α=3(4k+12k)θ4m=12kmθ
⇒d2θdt2+12kmθ=0⇒Equation of SHM
ω=2√3km⇒T1=π√m3k

When the rod moves leftward of line AB, spring of spring constant k2 will no play any role in the motion of the rod, so
mL2α3=kL2θ⇒α=3kmθ⇒(d2)θ)dt2+3kmθ=0
⇒T2=π√m3k
T=12(T1+T2)=3π2√m3k
(##FIT_JEE_PHY_GMP_ASS_E01_281_S02##)
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason15videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question58videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question2videos
GRAVITATION
Similar Questions
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
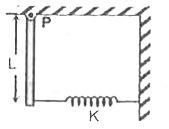 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A weightless spring of length 60 cm and force constant 200 N/m is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
Aπ20sBπ10sCπ5sDπ√200s - Question 2 - Select One
A rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
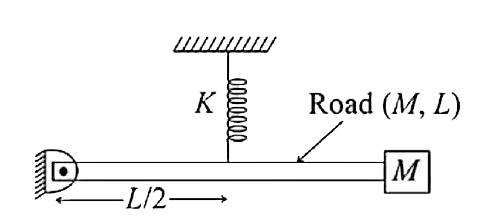 A3MgKBMgKC2MgKD4MgK
A3MgKBMgKC2MgKD4MgK - Question 3 - Select One
A weightless spring of length 60 cm and force constant 100Nm−1 is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
Aπ20 sBπ10 sCπ5 sDπ√200 s
A uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angular velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).
 View Solution
View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View Solution

