A particle is movbed from (0,0)→(a,a) under a force F=(x2ˆi+y3ˆj) from two paths. Path 1 si OP and Path 2 is OQP. Let W1 and W2 be the work done by this force in these two paths. Then
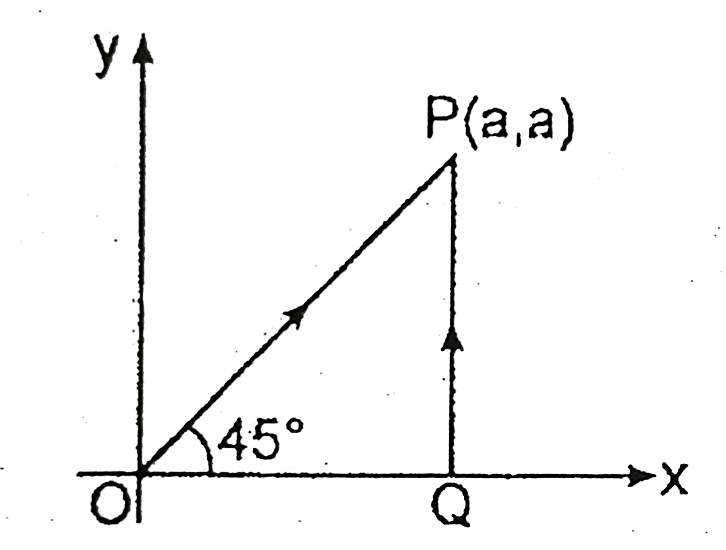
W1=W2
W1=2W2
W2=2W2
W2=4W1
The correct Answer is:A
A particle…………
The force is constant and hence conservative
∴W1=W2
Similar Questions
(a) A particle is acted upon by a force →F given by →F=Acosωtˆi+Bˆk and its position vector →r=a[(cos)(ωt)ˆi+sin(ωt)ˆj]+12bt2ˆk. Find the work done on the particle by the force →F from time t=π/2ω to time t=π/ω.
(b) A particle moves under a force →F=xyˆi+y2ˆj and traverses along a path y=4x+1. Find the work done by the force when the particle is displaced from the point P(1, 5) to Q(2, 9).
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
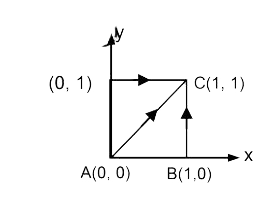
View Solution
Knowledge Check
A particle is moved from (0, 0) to (a, a) under a force a F=(3ˆi+4ˆj) from two paths. Path 1 is OP and path 2 is OPQ. Let W1 and W2 be the work done by this force in these two paths. Then,
AW1=W2BW1=2W2CW2=2W1DW2=4W1A particle is moved from (0,0) to (a, a) under a force →F=(3ˆi+4ˆj) from two paths. Path 1 is OP and path 2 is OQP. Let W and W be the work done by this force in these two paths.Then
 AW = W2BW = 2WCW = 2WDW = 4W
AW = W2BW = 2WCW = 2WDW = 4WA particle is moved from (0,0)to (a,a) under a force ¯¯¯F=(3ˆi+4ˆj) and path 2isOQP.Let W1andW2 be the work by done this force in these to paths .Then .
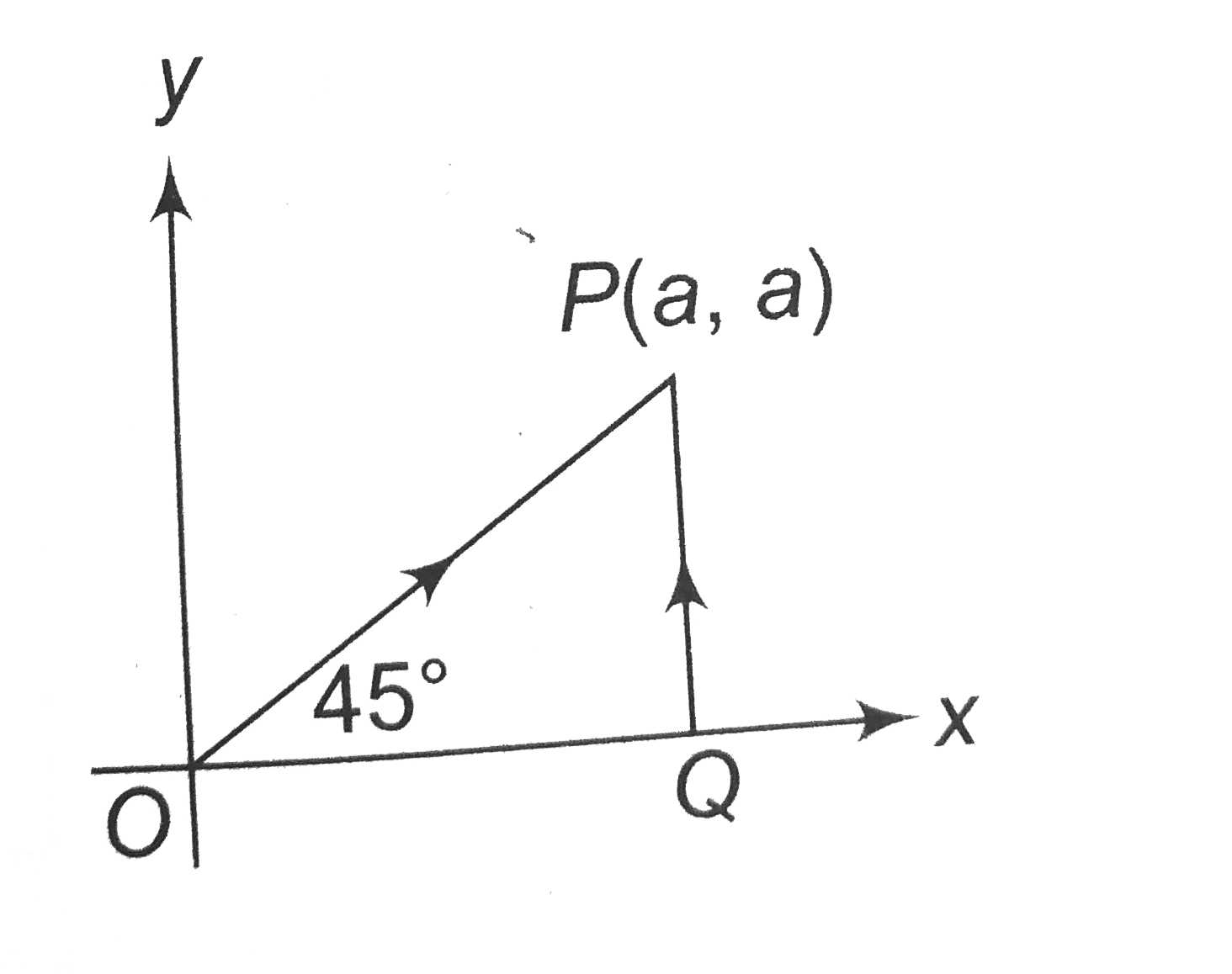 AW1=W2BW1=2W2CW2=2W1DW2=4W1
AW1=W2BW1=2W2CW2=2W1DW2=4W1
A particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
View SolutionA given mass of gas expands from state A to state B by three paths 1, 2 and 3 as shown in the figure
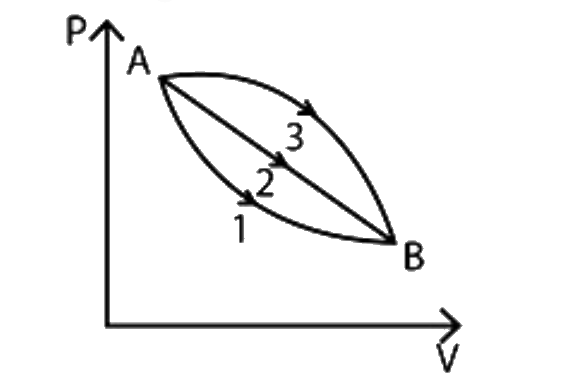
If w1,w2andw3 respectively are be the works done by the gas along three paths, then
View SolutionA given mass of a gas expands from the state A to the state B by three paths 1,2 and 3 as shown in the figure, If W1,W2 and W3 respectively be the work done by the gas along the three paths then

View SolutionA particle is displaced from a position (2ˆi−ˆj+ˆk) to another position (3ˆi+2ˆj−2ˆk) under the action of the force (2ˆi+ˆj−ˆk). The work done by the force in arbitrary unit is
View Solution
