A system is taken from state A to state B along two different paths 1 and 2 . The heat absorbed and work done by the system along these two paths are Q1 and W1 and W2 respectively.
Q1=Q2
W1=W2
Q1−W1=Q2−W2
Q1+W1=Q2+W2
To solve the problem, we need to analyze the relationship between heat absorbed (Q) and work done (W) along two different paths when a system transitions from state A to state B. We will use the first law of thermodynamics to derive the necessary relationships.
1. Understanding the First Law of Thermodynamics:
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat absorbed (Q) by the system minus the work done (W) by the system. Mathematically, it can be expressed as:
ΔU=Q−W
2. Applying the First Law for Path 1:
For the first path (Path 1), we can express the first law as:
ΔU=Q1−W1
Rearranging gives us:
Q1=ΔU+W1(1)
3. Applying the First Law for Path 2:
For the second path (Path 2), we similarly apply the first law:
ΔU=Q2−W2
Rearranging gives us:
Q2=ΔU+W2(2)
4. Recognizing that Internal Energy Change is Path Independent:
The change in internal energy (ΔU) depends only on the initial and final states of the system and is independent of the path taken. Therefore, ΔU is the same for both paths:
ΔU=UB−UA(constant for both paths)
5. Subtracting the Two Equations:
Now, we can subtract equation (1) from equation (2):
Q1−Q2=(W1−W2)
Rearranging this gives us:
Q1−W1=Q2−W2
6. Conclusion:
The final relationship we derived is:
Q1−W1=Q2−W2
This shows that the difference between heat absorbed and work done is the same for both paths.
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat absorbed (Q) by the system minus the work done (W) by the system. Mathematically, it can be expressed as:
ΔU=Q−W
For the first path (Path 1), we can express the first law as:
ΔU=Q1−W1
Rearranging gives us:
Q1=ΔU+W1(1)
For the second path (Path 2), we similarly apply the first law:
ΔU=Q2−W2
Rearranging gives us:
Q2=ΔU+W2(2)
The change in internal energy (ΔU) depends only on the initial and final states of the system and is independent of the path taken. Therefore, ΔU is the same for both paths:
ΔU=UB−UA(constant for both paths)
Now, we can subtract equation (1) from equation (2):
Q1−Q2=(W1−W2)
Rearranging this gives us:
Q1−W1=Q2−W2
The final relationship we derived is:
Q1−W1=Q2−W2
This shows that the difference between heat absorbed and work done is the same for both paths.
Topper's Solved these Questions
Similar Questions
A system is taken from state "A" to state "B" along two different paths,"1" and "2." The heat absorbed and work done by the system along these two paths are Q1 and Q2 and W1 and W2 respectively
View SolutionA system is taken from state a to state c along the path adc (figure). The amount of heat absorbed is 10cals and work done on the gas is 138J. Calculate the work done on//by the gas when 20cals of heat are absorbed in taking the system from state a to state c along the path abc

View Solution
Knowledge Check
A system is taken from state A to state N along two different paths 1 and 2. The heat absorbed and work done by system along these two paths are Q1 and Q2, and W1 and W2 respectively. Then
AQ1=Q2BW1=W2CQ1−W1=Q2−W2DQ1+W1=Q2+W2A system is taken from state A to B through three different paths 1,2 and 3. The work done is maximum is :
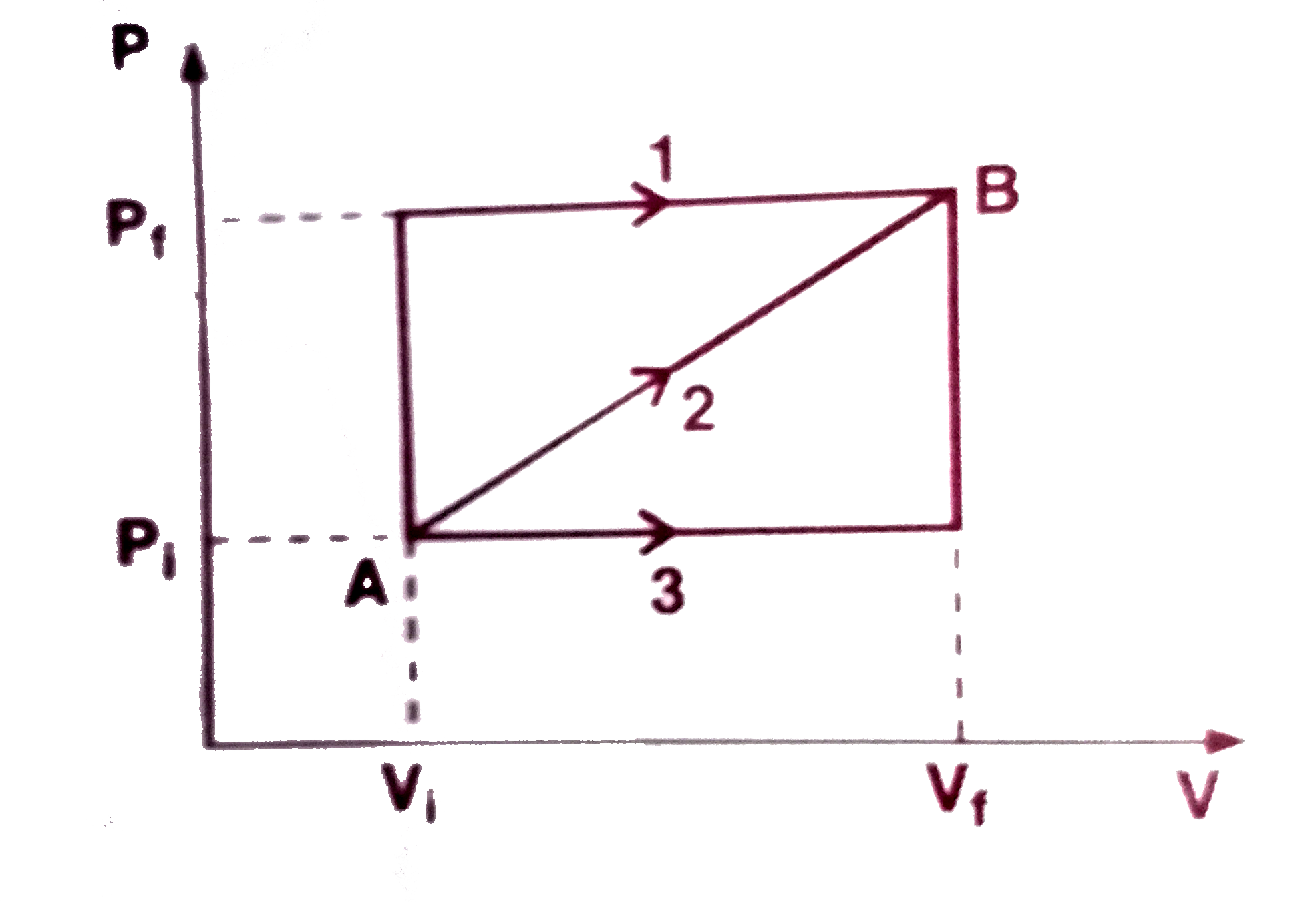 Aprocess 1Bprocess 2Cprocess 3Dequal in all magnitude
Aprocess 1Bprocess 2Cprocess 3Dequal in all magnitudeWhen a system is taken from stata a to state b along the path acb as shown in figure, 60 J of heat flows into the system and 30 J of work is done by the system. Along the path adb, if the work done by the system is 10 J, heat flow into the system is
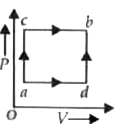 A100 JB20 JC80 JD40 J
A100 JB20 JC80 JD40 J
A thermodynamic system is taken from an initial state I with internal energy Ui=−100J to the final state f along two different paths iaf and ibf, as schematically shown in the figure. The work done by the system along the pat af, ib and bf are Waf=200J,Wib=50JandWbf=100J respectively. The heat supplied to the system along the path iaf, ib and bf are Qiaf,Qib,Qbf respectively. If the internal energy of the system in the state b is Ub=200JandQiaf=500J, The ratio QbfQib is

View SolutionWhen a thermodynamic system is taken from an initial state I to a final state F along the path IAF, as shown in Fig. the heat energy absorbed by the system is Q=55J and work done by the system is W=25J. If the same system is taken along the path IBF, the value of Q=35J.
(a) If W=−15J for the curved path FI, how much heat energy is lost by the system along this path ?
(b) If U1=10J, what is UF ?
(d) If UB=20J, what is Q for the process BF and IB ?
View SolutionIn given figure, when a thermodynamic system is taken from state A to state B via path ACB,100 cal of heat given to the system and 60cal work is done by the gas. Along the path ADB, the work done by the gas is 20cal. Find the heat flowing into the system in this case?
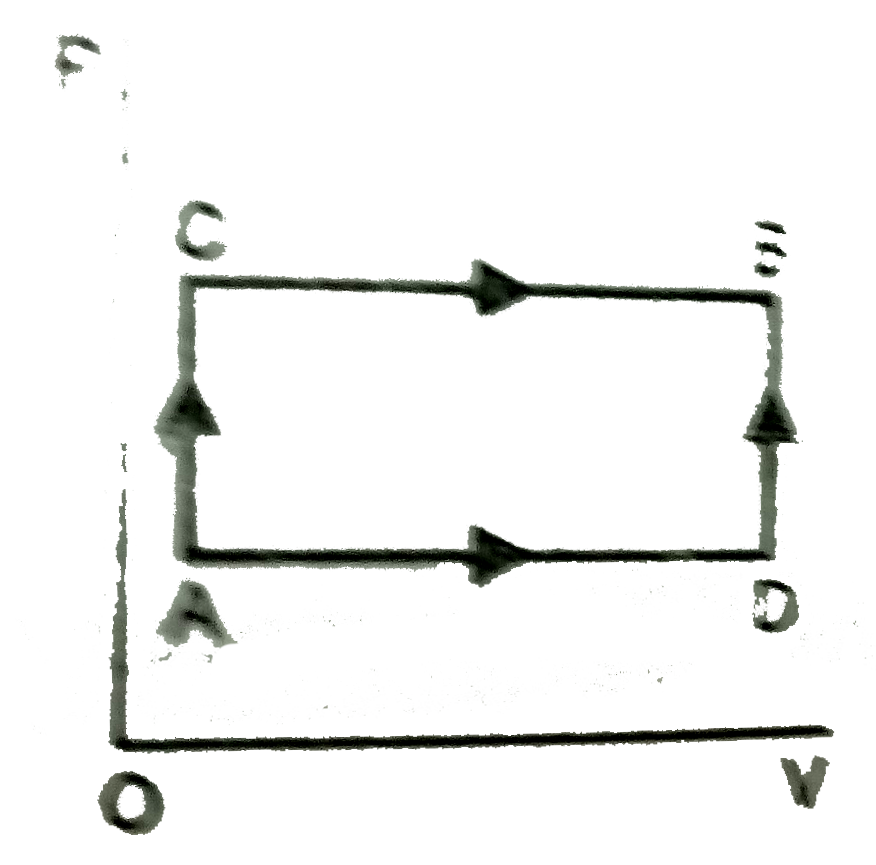
View SolutionWhen a system is taken from state i to state f along the path iaf, it is found that Q=50calandW=20cal. Along the path ibf Q=36cal. W along the path ibf is

View SolutionAn ideal gas can be taken form initial state 1 to final state 2 by two different process. Let ΔQ and W represent the heat given and work done by the system. Then which quantities is/are same in both process (where ΔU= internal energy of gas)
View Solution

