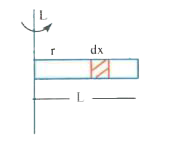
A uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
The correct Answer is:ρω2L3Y
To solve the problem of finding the increase in length of a uniform rod of length L when it is rotated about a vertical axis through one of its ends with an angular speed ω, we can follow these steps:
Step 1: Understand the Forces Acting on the Rod
When the rod is rotated, each small element of the rod experiences a centrifugal force due to the rotation. The centrifugal force acting on an infinitesimal element dx at a distance x from the axis of rotation is given by:
dF=ρAdx⋅ω2x
where ρ is the density of the rod, A is the cross-sectional area, and dx is the infinitesimal length of the element.
Step 2: Calculate the Tension in the Rod
The tension T at a distance x from the end of the rod can be expressed as the integral of the centrifugal force from x to L:
T(x)=∫LxdF=∫LxρAω2xdx
This integral will give us the total tension at point x.
Step 3: Evaluate the Integral
The integral can be evaluated as follows:
T(x)=ρAω2∫Lxxdx=ρAω2(x22)Lx=ρAω2(L22−x22)
Thus, we have:
T(x)=ρAω22(L2−x2)
Step 4: Calculate Stress and Strain
The stress σ at point x is given by:
σ=T(x)A=ρω22(L2−x2)
The strain ϵ is related to stress by Young's modulus Y:
σ=Yϵ⇒ϵ=σY=ρω22Y(L2−x2)
Step 5: Relate Strain to Change in Length
The change in length dL of an infinitesimal segment dx can be expressed as:
dL=ϵdx=ρω22Y(L2−x2)dx
Step 6: Integrate to Find Total Increase in Length
To find the total increase in length ΔL, we integrate dL from x=0 to x=L:
ΔL=∫L0dL=∫L0ρω22Y(L2−x2)dx
Evaluating this integral:
ΔL=ρω22Y(L2x−x33)L0=ρω22Y(L3−L33)=ρω2L32Y⋅23=ρω2L33Y
Final Result
Thus, the increase in length of the rod is:
ΔL=ρω2L33Y
When the rod is rotated, each small element of the rod experiences a centrifugal force due to the rotation. The centrifugal force acting on an infinitesimal element dx at a distance x from the axis of rotation is given by:
dF=ρAdx⋅ω2x
where ρ is the density of the rod, A is the cross-sectional area, and dx is the infinitesimal length of the element.
The tension T at a distance x from the end of the rod can be expressed as the integral of the centrifugal force from x to L:
T(x)=∫LxdF=∫LxρAω2xdx
This integral will give us the total tension at point x.
The integral can be evaluated as follows:
T(x)=ρAω2∫Lxxdx=ρAω2(x22)Lx=ρAω2(L22−x22)
Thus, we have:
T(x)=ρAω22(L2−x2)
The stress σ at point x is given by:
σ=T(x)A=ρω22(L2−x2)
The strain ϵ is related to stress by Young's modulus Y:
σ=Yϵ⇒ϵ=σY=ρω22Y(L2−x2)
The change in length dL of an infinitesimal segment dx can be expressed as:
dL=ϵdx=ρω22Y(L2−x2)dx
To find the total increase in length ΔL, we integrate dL from x=0 to x=L:
ΔL=∫L0dL=∫L0ρω22Y(L2−x2)dx
Evaluating this integral:
ΔL=ρω22Y(L2x−x33)L0=ρω22Y(L3−L33)=ρω2L32Y⋅23=ρω2L33Y
Thus, the increase in length of the rod is:
ΔL=ρω2L33Y
Topper's Solved these Questions
- ELASTICITYBook:ARIHANTChapter:ELASTICITYExercise:Level 3
Explore 1 Video
- ELASTICITYBook:ARIHANTChapter:ELASTICITYExercise:Level 3
Explore 1 Video
- CALORIMETRYBook:ARIHANTChapter:CALORIMETRYExercise:Level 3
Explore 1 Video
- FIRST LAW OF THERMODYNAMICSBook:ARIHANTChapter:FIRST LAW OF THERMODYNAMICSExercise:Level 3
Explore 6 Videos
Similar Questions
A metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.
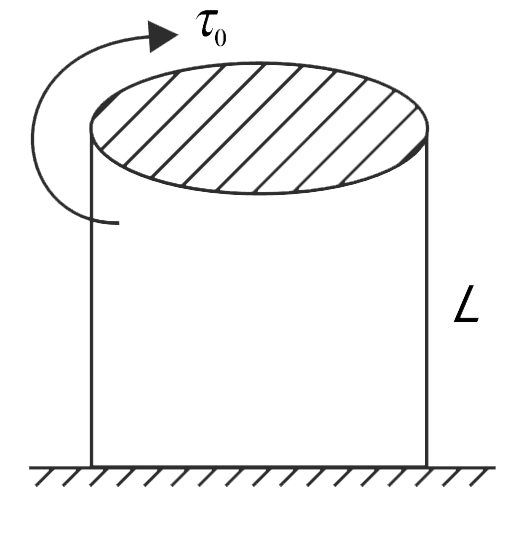
View SolutionA metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.

View SolutionA copper calorimeter has mass of 180 g and contains 450 g of water and 50 g of ice, all at 0∘C. Dry steam is passed into the calorimeter until a certain temperature (θ) is reached. The mass of the calorimeter and its contents at the end of the experiment increased by 25 g. Assume no heat loss to the surrounding and take specific heat capacities of water and copper to be 4200Jkg−1K−1 and 390Jkg−1K−1, respectively. Take specific latent heat of vaporization of water to be 3.36×105Jkg−1 and 2.26×106Jkg−1 respectively.
(a) Find the final temperature θ
(b) If steam enters into the system at a steady rate of 5g−1min, plot the variation of temperature of the system till final temperature θ is attained.
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity o in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA uniform rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is omega . Find increase in length of the rod, if rho and Y are the density and Young's modulus of the rod respectively,
View SolutionA uniform rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is ω . Find increase in length of the rod, if ρ and Y are the density and Young's modulus of the rod respectively,
View SolutionA thin uniform rod of length L and radius r rotates with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. The density of the material is ρ and Youngs modulus is Y. 1) Find tension in the rod at distance Y from the axis. 2) Find elongation of the rod
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(omega\) in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B . The rod begins rotating from rest. The angular velocity omega at angle theta is given as
View Solution