A thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]
![A thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C11_E01_013_Q01.png)
The correct Answer is:Mg16A
Step by step video, text & image solution for A thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Videos
- CALORIMETRYBOOK - ARIHANTCHAPTER - CALORIMETRYEXERCISE - Level 3
1 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
Similar Questions
A uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
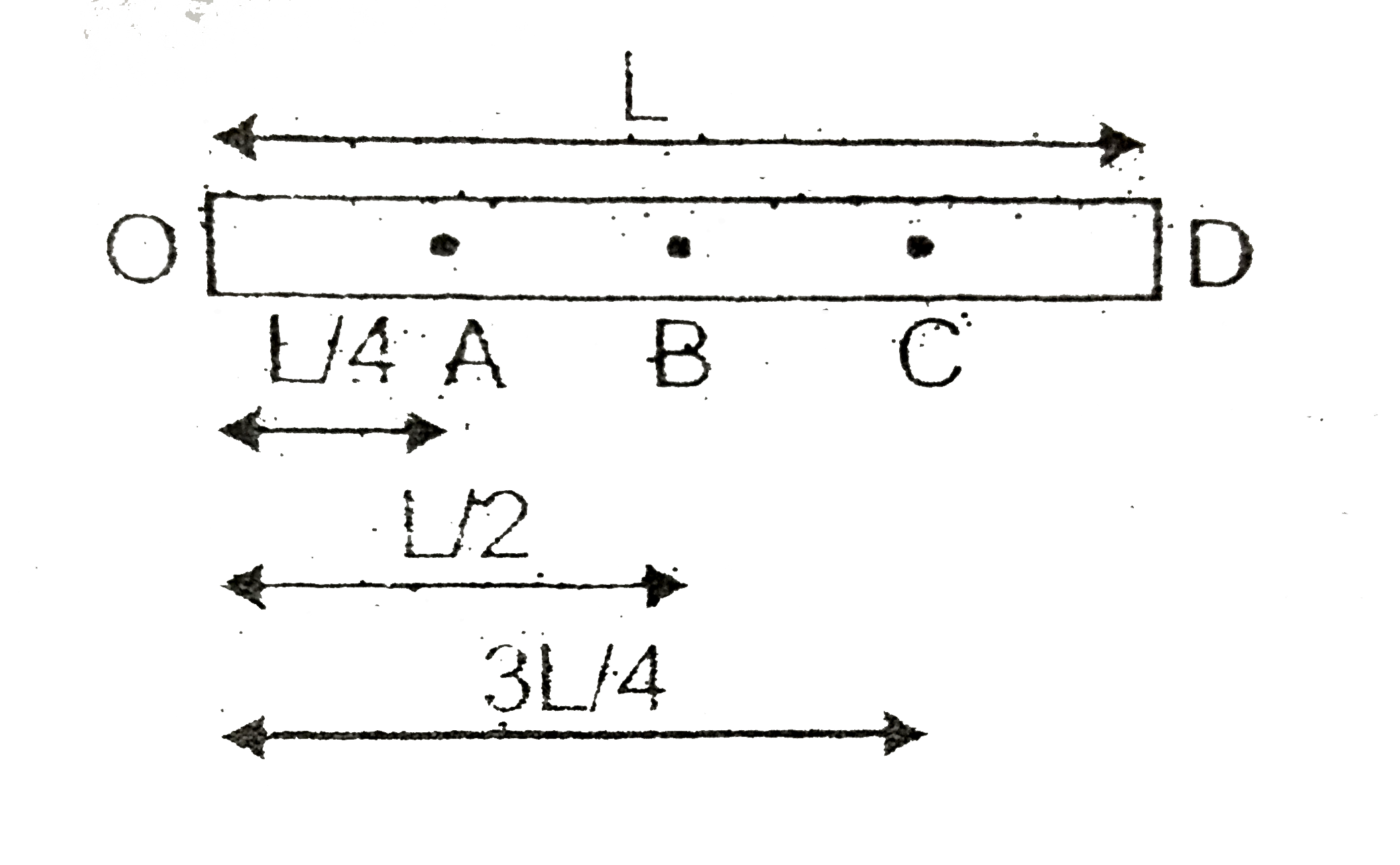
View SolutionA uniform rod is rotating about a horizontal axis as shown. The rod is hinged at one of the ends. The rod is released from a vertical position by slightly pushing it. As the rod moves from A to B
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
 A3g√10IB9g10lC9g5lD6g5√2I
A3g√10IB9g10lC9g5lD6g5√2I
Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
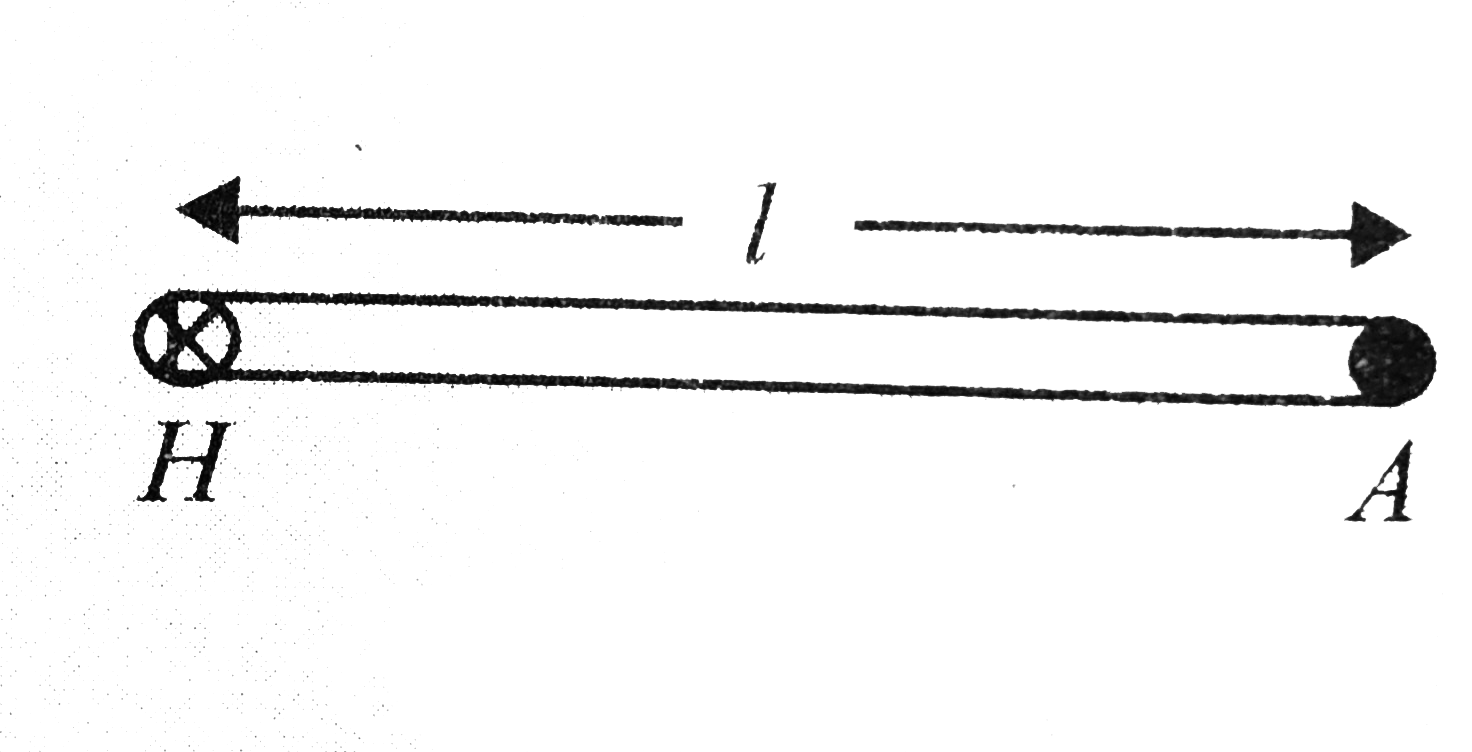
View SolutionA uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View Solution
