A thin uniform rod of length L and radius r rotates with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. The density of the material is $ρ$ and Youngs modulus is Y. 1) Find tension in the rod at distance Y from the axis. 2) Find elongation of the rod

Text Solution

Verified by Experts

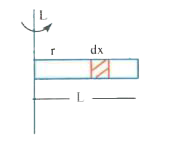
1) Consider and element dx at a distance from the axis of rotation.
2) The centripetal force on this portion is
$d t = d m r ω^{2} d T = (ρ A d r) r ω^{2}$
This force is provided by the tension in the rod
$\int d T = \overset{L}{\int_{r}} ρ A d r ω^{2}, T ρ A ω^{2} \overset{L}{\int_{r}} r d r, T = ρ A ω^{2} {[\frac{r^{2}}{2}]}_{r}^{L}$
$\Rightarrow T = \frac{ρ A ω^{2}}{2} [L^{2} - r^{2}] T = \frac{1}{2} ρ A ω^{2} (L^{2} - r^{2})$
(3) strain $= \frac{stress}{Y}$ If dy is the elongation in element of length dx
$\frac{d y}{d x} = \frac{T}{A Y} \Rightarrow d y = \frac{T d x}{A Y} \Rightarrow d y = \frac{\frac{1}{2} ρ A ω^{2} (L^{2} - r^{2}) d r}{A Y}$
$\int d y = \frac{ρ ω^{2}}{2 y} \overset{L}{\int_{0}} (L^{2} - r^{2}) d r \Rightarrow Δ L = \frac{ρ ω^{2}}{2 y} {[L^{2} r - \frac{r^{3}}{3}]}_{0}^{L}$
$Δ L = \frac{ρ ω^{2}}{2 Y} [L^{2} - \frac{L^{3}}{3}] \Rightarrow Δ L = \frac{ρ ω^{2}}{2 y} [\frac{2 L}{3}], Δ L \equiv \frac{ρ ω^{2} L^{3}}{3 Y}$

Updated on:21/07/2023

A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity $ω$ in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
A $\frac{m ω^{2} l^{2}}{6 A Y}$
B $\frac{m ω^{2} l^{2}}{3 A Y}$
C $\frac{m ω^{2} l^{2}}{A Y}$
D $\frac{m ω^{2} l^{2}}{2 A Y}$
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all points
Bdifferent at differen points and maximum at centre of rod
Cdifferent at different points and minimum at axis of rotation.
Ddifferent at different points and maximum at axis of rotation