A rigid cylindrical container has inner radius r. A cork having radius r+Δr and length L is to be fitted so as to close the container. Uniform pressure (ΔP) is needed on the curved cylindrical surface of the cork. Poisson’s ratio of a cork is almost zero, and its bulk modulus is B.
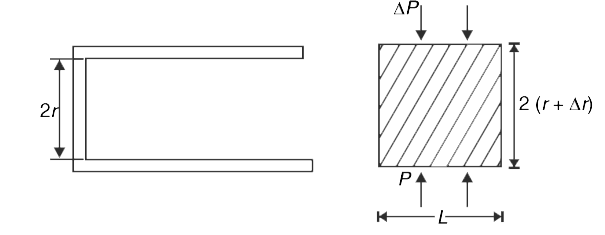
(a) Calculate ΔP
(b) After the cork is fitted how much force will be needed to pull it out of the container? Coefficient of friction between the container and the cork is μ.
The correct Answer is:(a) ΔP=2BΔrr , (b) F=4πμBLΔr
Step by step video, text & image solution for A rigid cylindrical container has inner radius r. A cork having radius r + Delta r and length L is to be fitted so as to close the container. Uniform pressure (Delta P) is needed on the curved cylindrical surface of the cork. Poisson’s ratio of a cork is almost zero, and its bulk modulus is B. (a) Calculate Delta P (b) After the cork is fitted how much force will be needed to pull it out of the container? Coefficient of friction between the container and the cork is mu. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Video
- ELASTICITYBOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 3
1 Video
- CALORIMETRYBOOK - ARIHANTCHAPTER - CALORIMETRYEXERCISE - Level 3
1 Video
- FIRST LAW OF THERMODYNAMICSBOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 3
6 Videos
Similar Questions
If R be the circum radius and r the in radius of a triangle ABC, show that R≥2r
View SolutionA bottle has an opening of radius a and length b. A cork of length b and radius (a+ΔA) is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and frictional coefficient between the bottle and cork is ? then the force needed to push the cork into the bottle is :
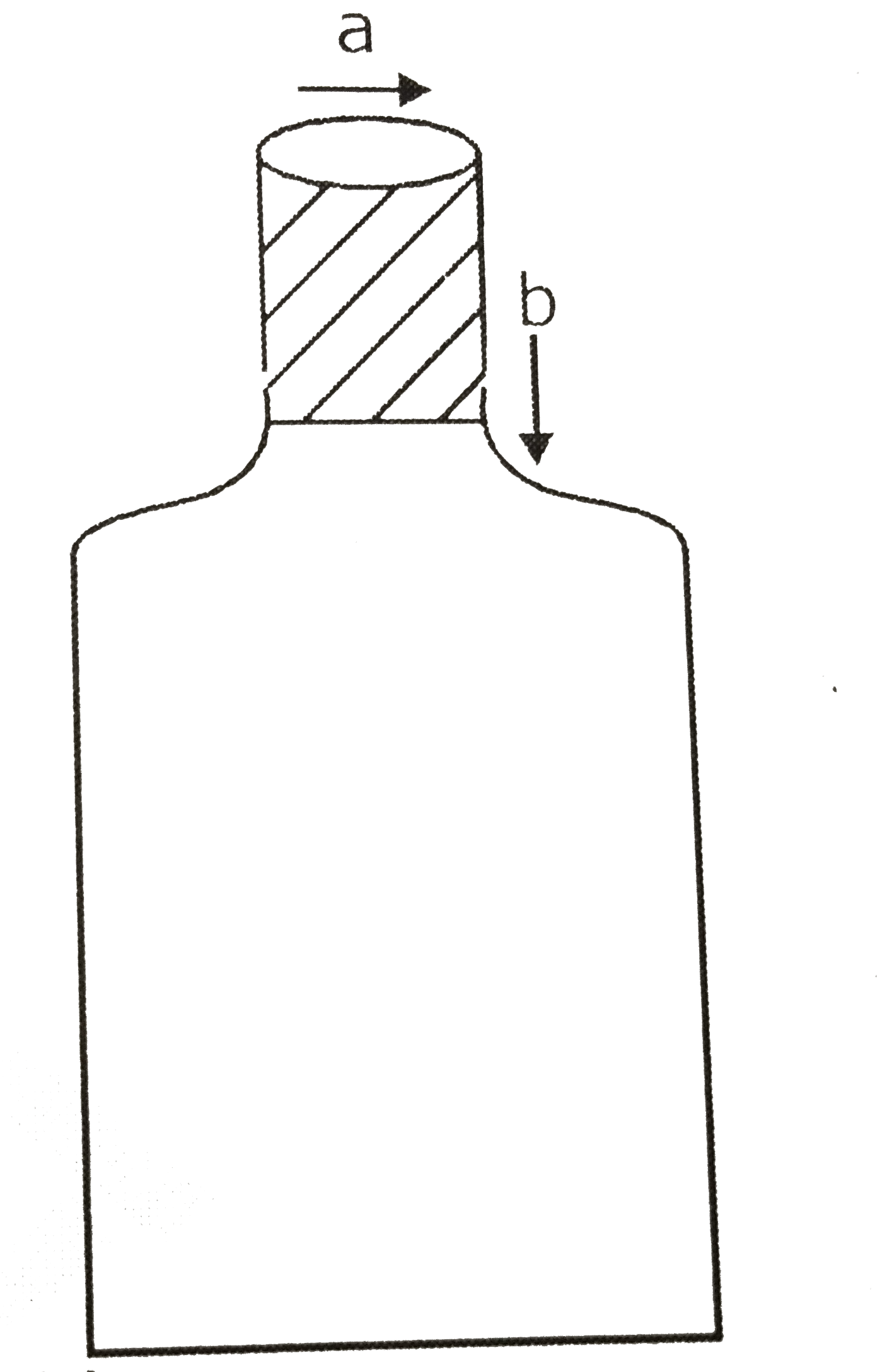
View Solution
Knowledge Check
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is ρ. The resistance of the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρlAt places, the cork contains aerating pores called -
AStomataBLenticelsCHydathodeDPneumatophoreIf R is the radius of the circumcircle of the ΔABCandΔ is its area then
AR=a+b+c2BR=a+b+cΔCR=abc4ΔDR=abcΔ
A cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)
View Solutionif radius of a sphere is r with error δr,andS is its surface area, thn approximate error in
View SolutionThe ratio of modulus of rigidity to bulk modulus for a Poisson's ratio of 0.15 would be
View SolutionFind the ratio of circum radius (R) to inradius (r) of a triangle whose sides are 4,6 and 8.
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View Solution