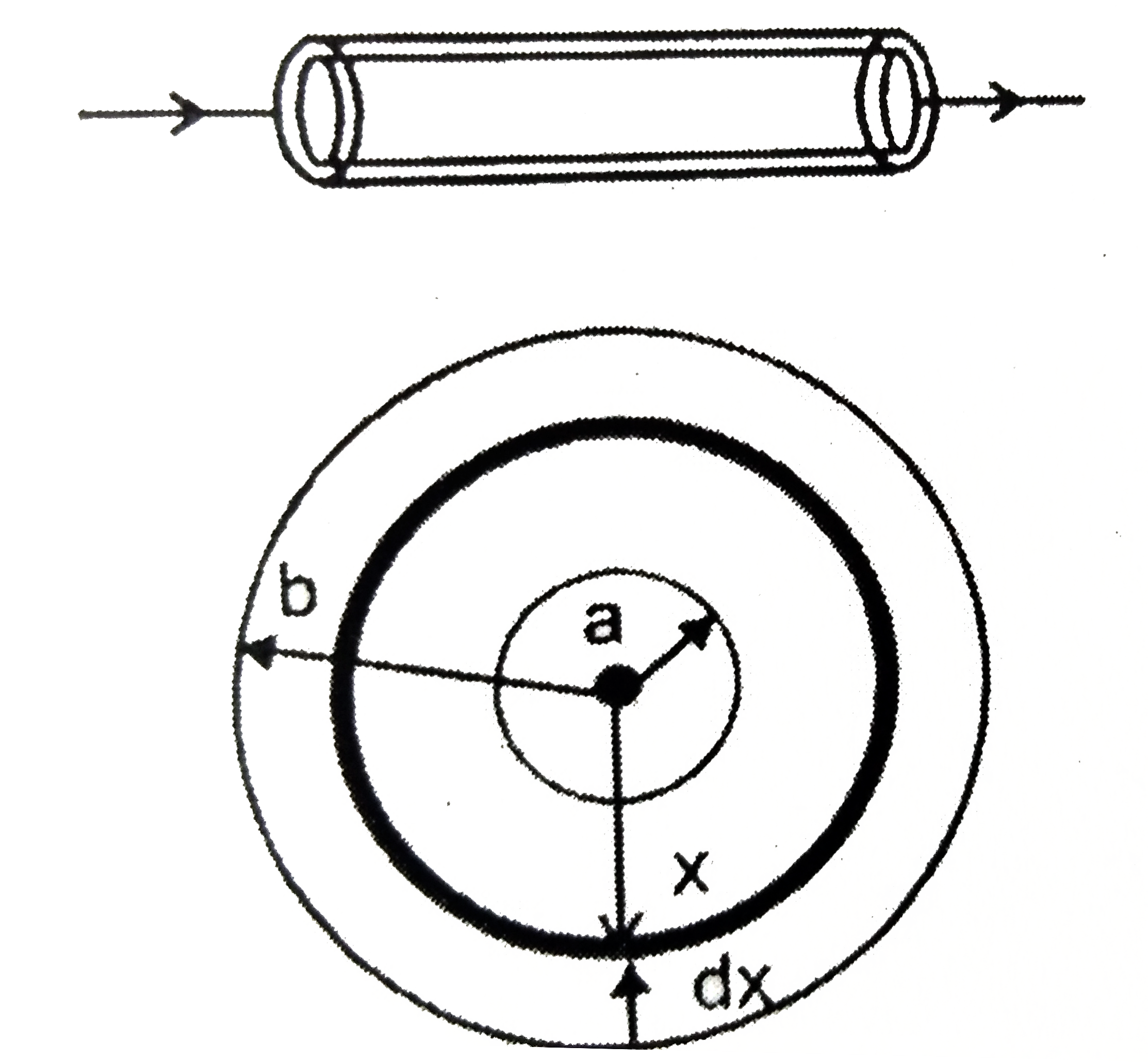
A cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)
(a) A=π(b2−a2)
R=plπ(b2−a2)
(b) dR=ρdx2πxl
for a section taken at distance x form centre.
dR=ρ2πldxx
⇒R=∫dR=ρ2πla∫bdxx=lnba
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-1)
Explore 46 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise-1 (Part-2)
Explore 49 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- COMMUNICATION SYSTEMSBook:RESONANCEChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP.No.71
Explore 1 Video
Similar Questions
A cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)
View SolutionA hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length 1 is as shown in figure. What is the net resistance between the inner and outer surfaces?
View Solution
Knowledge Check
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is ρ. The resistance of the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρlSphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
Ap4π(1a−1b)Bp2π(1a−1b)Cp3π(2a−1b)Dp2π(22a−1b)The hollow cylinder of length l and inner and outer radius R1 and R2 respectively. Find resistance of cylinder if current flows radially outward in the cylinder. Resistivity of material of cylinder id ρ .
A((ρπelln(R1R2))B((ρ4πelln(R2R1))C((ρ3πelln(R2R1))D((ρ2πelln(R2R1))
A cylindrical wire of length L and radius r has a resistance R. The resistance of another wire of the same material but half its length and half its radius will be:
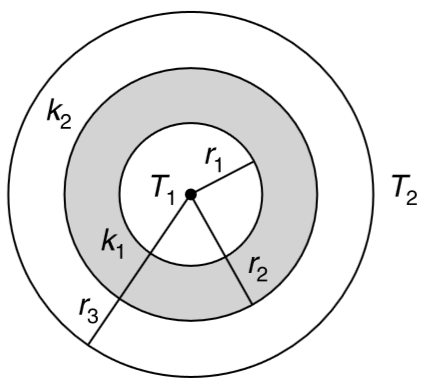
View Solution(i) A cylindrical pipe of length L has inner and outer radii as a and b respectively. The inner surface of the pipe is at a temperature T1 and the outer surface is at a lower temperature of T2. Calculate the radial heat current if conductivity of the mate- rial is K.
(ii) A cylindrical pipe of length L has two layers of material of conduc- tivity K1 and K2. (see figure). If the inner wall of the cylinder is maintained at T1 and outer surface is at T2(<T1), calcu- late the radial rate of heat flow.
View SolutionA conducting spherical shell having inner radius a and outer radius b carries a net charge Q. If a point charge q is placed at the centre of this shell, then the surface charge density on the outer surface of the shell is given as:
View Solution
A cylindrical conductor of length l and inner radius R1 and outer radius R2 has specific resistance ρ. A cell of emf ε is connected across the two lateral faces of the conductor. Find the current drown from the cell.
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View Solution

