A resistance coil of resistance r connected to an external battery, is placed inside an adiabatic cylinder fitted with a frictionless platon of mass m and same area A. Initially cylinder contains one mole of ideal gas he. A current through the coil such that temperature of gas varies as $T = T_{0} + at + {bt}^{2},$ keeping pressure constant with time t. Atosphere pressure above piston is $P_{0}$ . Find

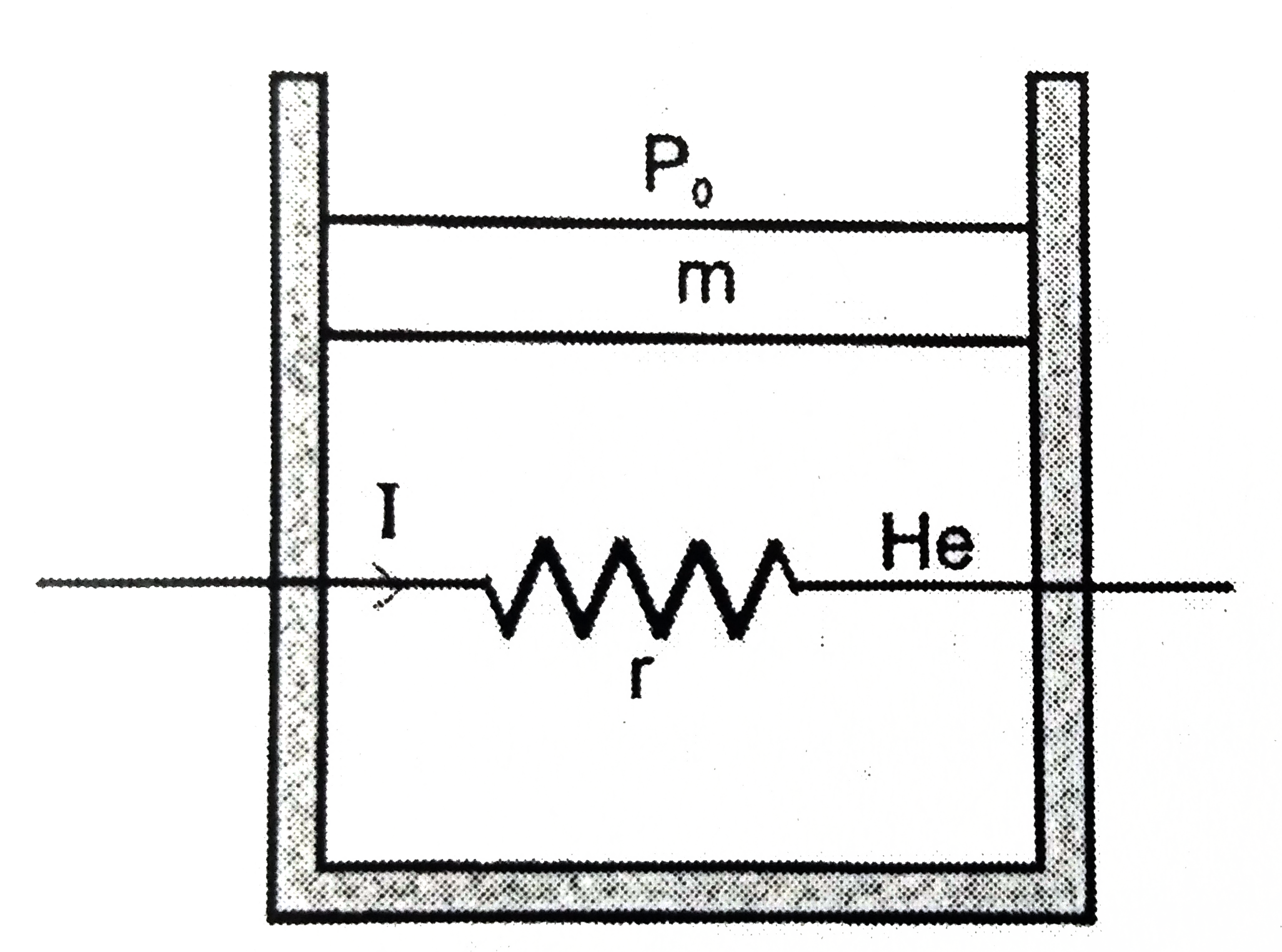
(a) Current l flowing through the coil as function of time and
(b) Speed of piston as function of time.

Video Solution

Text Solution

Verified by Experts

Heat produced by coil inside the cylinder in time dt is
$d Q = l^{2} r d t \dots \dots \dots \dots \dots \dots (i)$
(a) As we know
$\Rightarrow d Q = n C_{P} d T$
$I^{2} r d t = \frac{5 R}{2} d T (C_{P} = \frac{5 R}{2})$
Here $T = T_{0} + at + b t^{2} \Rightarrow \frac{d T}{d t} = (a + 2 b t)$
$I = \sqrt{[\frac{5 R}{2 r} (2 b t + a)]} ... ... ... ... (i i)$
$(C_{p} = \frac{5 R}{2})$
Pressure is constant $P V = R T \Rightarrow P d V = R d T$
PAdx=RdT
$Velocit v = \frac{d x}{d t} = \frac{R}{P A}, \frac{d T}{d t} = \frac{R}{P A} (2 b t + a) (here P_{0} A + m g = P A)$
$= \frac{R}{P_{0} A + m g} (2 b t + a)$

Updated on:21/07/2023

A resistance coil, connected to an external battery is placed inside an adiabatic cylinder filled with frictionless piston of mass $m$ and containing an ideal gas. A current $i$ flows through the coil, which has resistance $R$ . The speed with which the piston must move in order to keep the temperature of the gas constant will be

A $i^{2} R / m g$
B $i R / m g$
C $0$
DData is insufficient.
A heating element of piston resistance r is fitted inside an adiabatic cylinder which carries a frictionless piston of mass m and crosssection A as shown in diagram. The cylinder contains one mole of an ideal diatomic gas. The current flows through the element such that the temperature rises with time t as $Δ T = a l p a h t + \frac{1}{2} β t^{2}$ ? ( $α$ and $β$ are constants), while pressure remains constant. The atmospheric pressure above the piston is $P_{0}$ . Then
Athe rate of increase in internal energy is $\frac{5}{2} R (α + β t)$
Bthe current flowing in the element is $\sqrt{\frac{5}{2 r} R (α + β t)}$
Cthe piston moves upwards with constant acceleration,
Dthe piston moves upwards with constant speed.
A coil resistance R and inductance L is connected to a battery of emf E volt. The final current in the coil is
A $\frac{E}{R}$
B $\frac{E}{L}$
C $\sqrt{(\frac{E}{R^{2} + L^{2}})}$
D $\sqrt{(\frac{E L}{R^{2} + L^{2}})}$