Figure shows a conductor of length l having a circular cross-section. The radius of cross-section varies linearly from a to b. Find the resistance of the conductor. ltbtgt

Video Solution

Text Solution

Verified by Experts

In this problem cross-section area is variable so we can't apply formula $(R = \frac{ρ l}{A})$ directly.

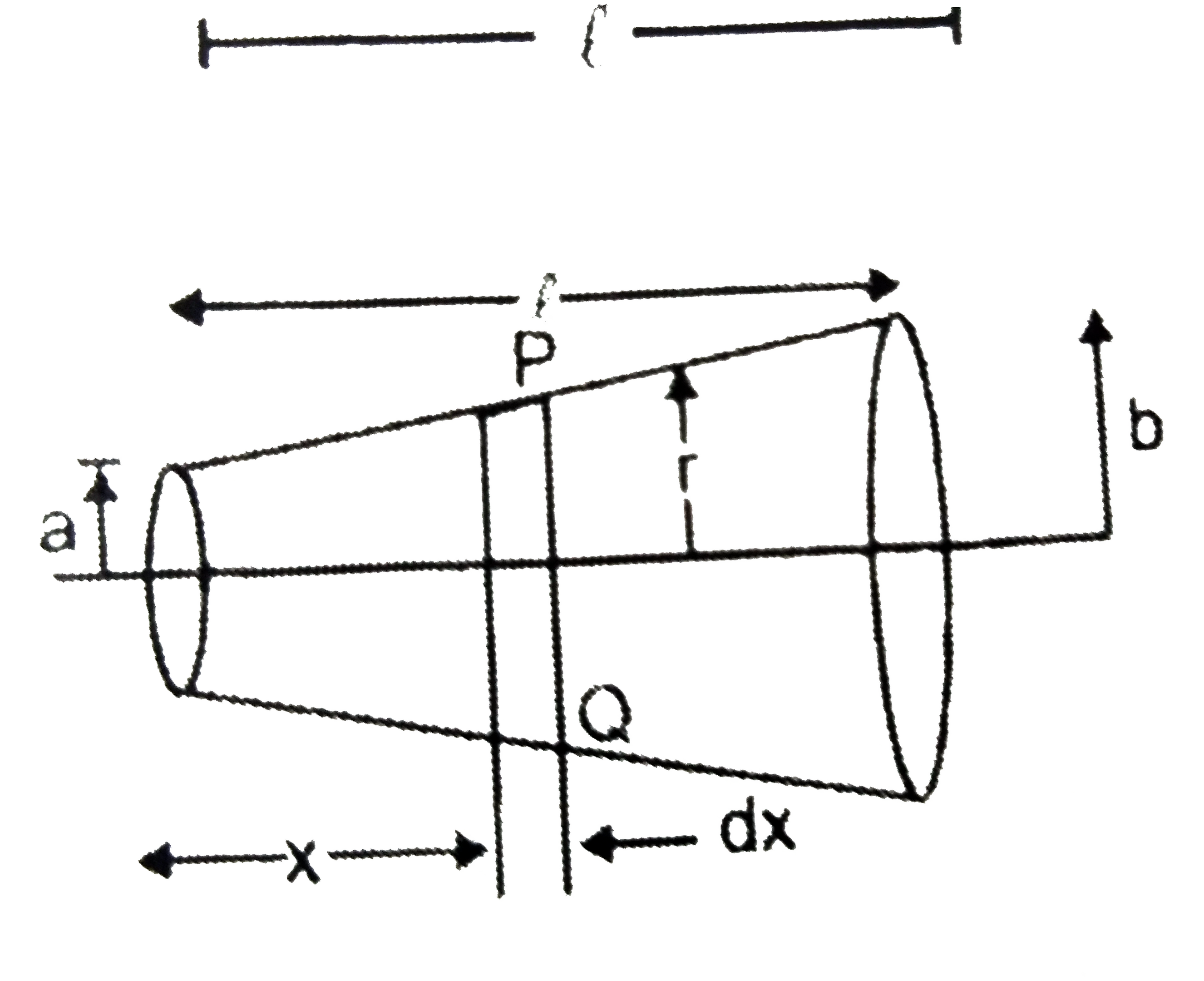
So we assume elementary strip 'PQ' of thickness dx and radius r resistance of this strip is :
$d R = \frac{ρ d x}{π r^{2}}$
$Bt grometry \frac{r - a}{x} = \frac{b - a}{t} \Rightarrow r = \frac{b - a}{l} x + a$
$Resistance of conductor is R = t \int 0 \frac{p d x}{π {\frac{b - a}{l} x + a}} \Rightarrow R = \frac{ρ l}{π a b}$

Updated on:21/07/2023

A conductor of length l and area of cross-section A has a resistance R then its specific resistance is
A $ρ = \frac{R A}{l}$
B $ρ = R A l$
C $ρ = \frac{l}{R A}$
D $ρ = \frac{R^{2} A}{l}$
The length and area of cross-section of a conductor are doubled, its resistance is
Aunchanged
Bhalved
Cdoubled
Dquadrupled
A conductor of length of l and area of cross section A has n number of electrons per unit volume of the conductor. The total charge carried by the conductor is
AnA/e
B $\frac{e}{n A l}$
C $\frac{n A l}{e}$
D $n \cdot e$