A spherical cavity is formed a solid sphere by removing mass from it. The resultant configuration is shown in figure. Find out the moment of inertia this configuration about the axis through centre of the solid sphere as shown . Take mass $M ($ uniform $)$ for the configuration and radius $R$ for solid sphere and radius $R / 2$ for cavity.

Video Solution

Text Solution

Verified by Experts

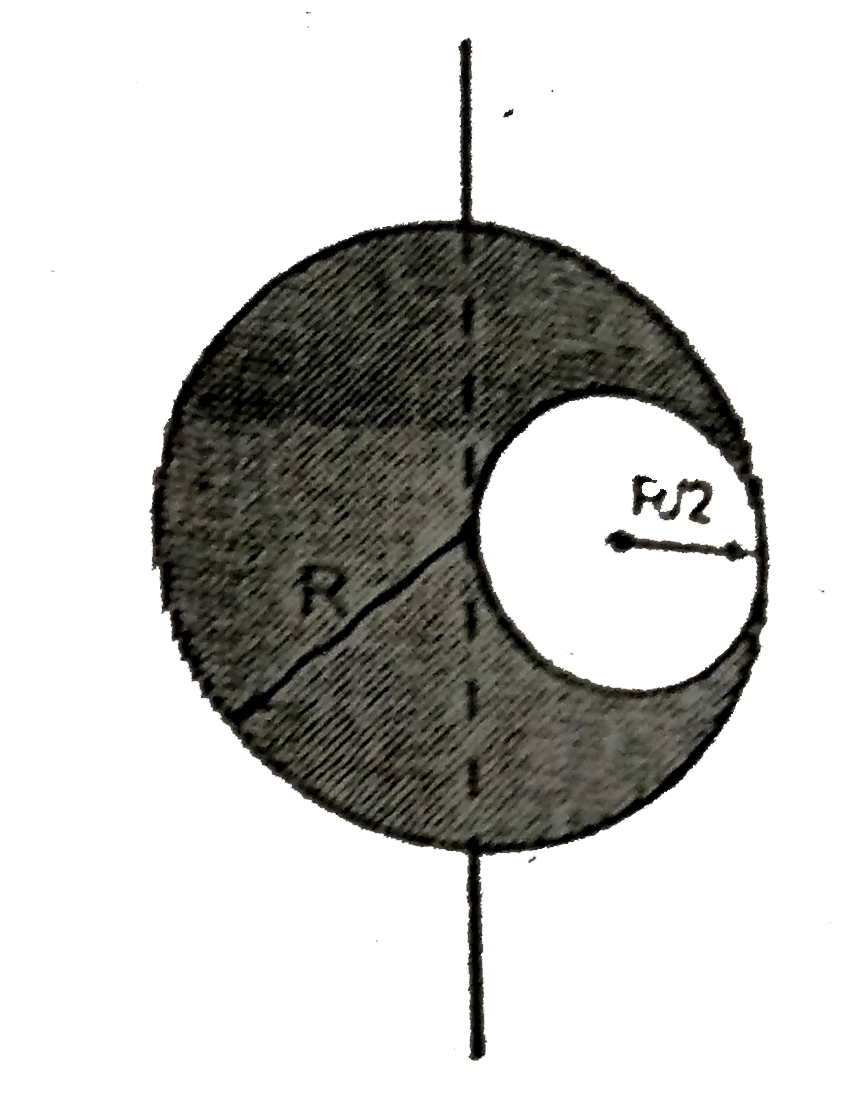
The correct Answer is: $I = \frac{57}{140} M R^{2}$

$ρ = \frac{M}{(4 / 3) π R^{3} - (4 / 3) π {(R / 2)}^{3}}$
$I = \frac{2}{5} M R^{2} - (\frac{2}{5} M_{2} {(\frac{R}{2})}^{2} + M_{2} {(\frac{R}{2})}^{2})$
$, I = \frac{57}{140} M R^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A hemi-spherical cavity is created in solid sphere (of radius $2 R$ ) as shown in the figure. Then

A $x_{c m} = - R / 15$
B $y_{c m} = - \frac{R}{40}$
C $z_{c m} = z e r o$
DNone of these
Question 2 - Select One
The moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A $\frac{2}{5} M R^{2}$
B $\frac{6}{3} M R^{2}$
C $\frac{4}{5} M R^{2}$
D $\frac{7}{5} M R^{2}$
Question 3 - Select One
A solid sphere and a hollow sphere are identical in mass and radius. The ratio of their moment of inertia about diameter is :
A $5 : 3$
B $1 : 1$
C $1 : 2$
D $3 : 5$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 58

Home
Ask Doubt
Profile