In the figure mA=mB=mC=60kg. The coefficient of friction between C and ground is 0.5B and ground is 0.3,A and B is 0.4.C is pulling the string with the maximum possible force without moving. Then the tension in the string connected to A will be 
120N
60N
100N
zero
The correct Answer is:D
Maximum frictional force between C and ground =300Nt
Max. frictional force between B and ground =360Nt
So man is unable to pull B Hence T=0
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 59
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 60
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 57
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
In the situation shown coefficient of friction between A and B is 0.5 and between B and C is 0.3 . Friction acting between B and C is xN then 9x7 is
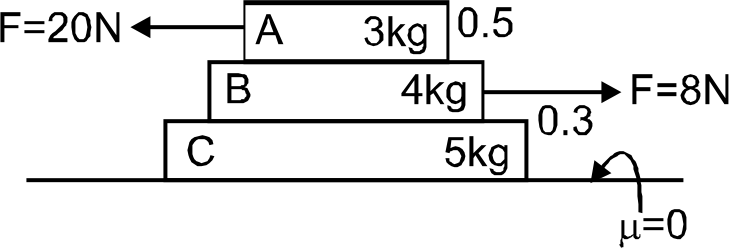
View SolutionIn the figure shown coefficient of friction between block A and ground is 0.4 and that between wedge and block B is zero. Wedge is fixed. Find tension is string and acceleration of block A if F = 28 N.

View Solution
Knowledge Check
In the figure shown m1=5kg,m2=10kg & friction coefficient between m1&m2 is μ=0.1 and ground is frictionless then :
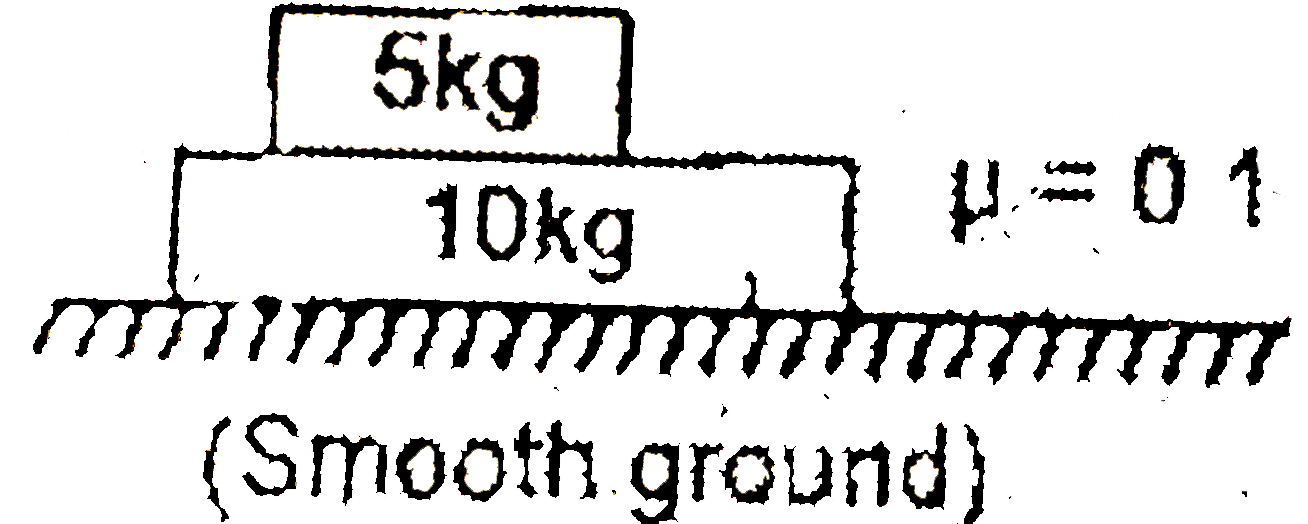 AIf a horizontal force F=20N is applied on m1 then the friction force acting on m2 is 5 N in the direction of FBMaximum amount of horizontal force that can be applied to m2 such that there is no relative motion between blocks is 15 NCIf a horizontal force F=20N is applied on m2 then friction force acting on m1 is 20/3 N in the direction of applied forceDMaximum amount of horizontal force that can be applied to m1 such that there is no relative motion between blocks is 8 N
AIf a horizontal force F=20N is applied on m1 then the friction force acting on m2 is 5 N in the direction of FBMaximum amount of horizontal force that can be applied to m2 such that there is no relative motion between blocks is 15 NCIf a horizontal force F=20N is applied on m2 then friction force acting on m1 is 20/3 N in the direction of applied forceDMaximum amount of horizontal force that can be applied to m1 such that there is no relative motion between blocks is 8 NIn the figure, m1=m2=10kg. The coefficients of friction between A,B and B, surface are 0.2. Find the maximum value of m3 so that no block slips ( All the pullies are ideal and strings are massless).
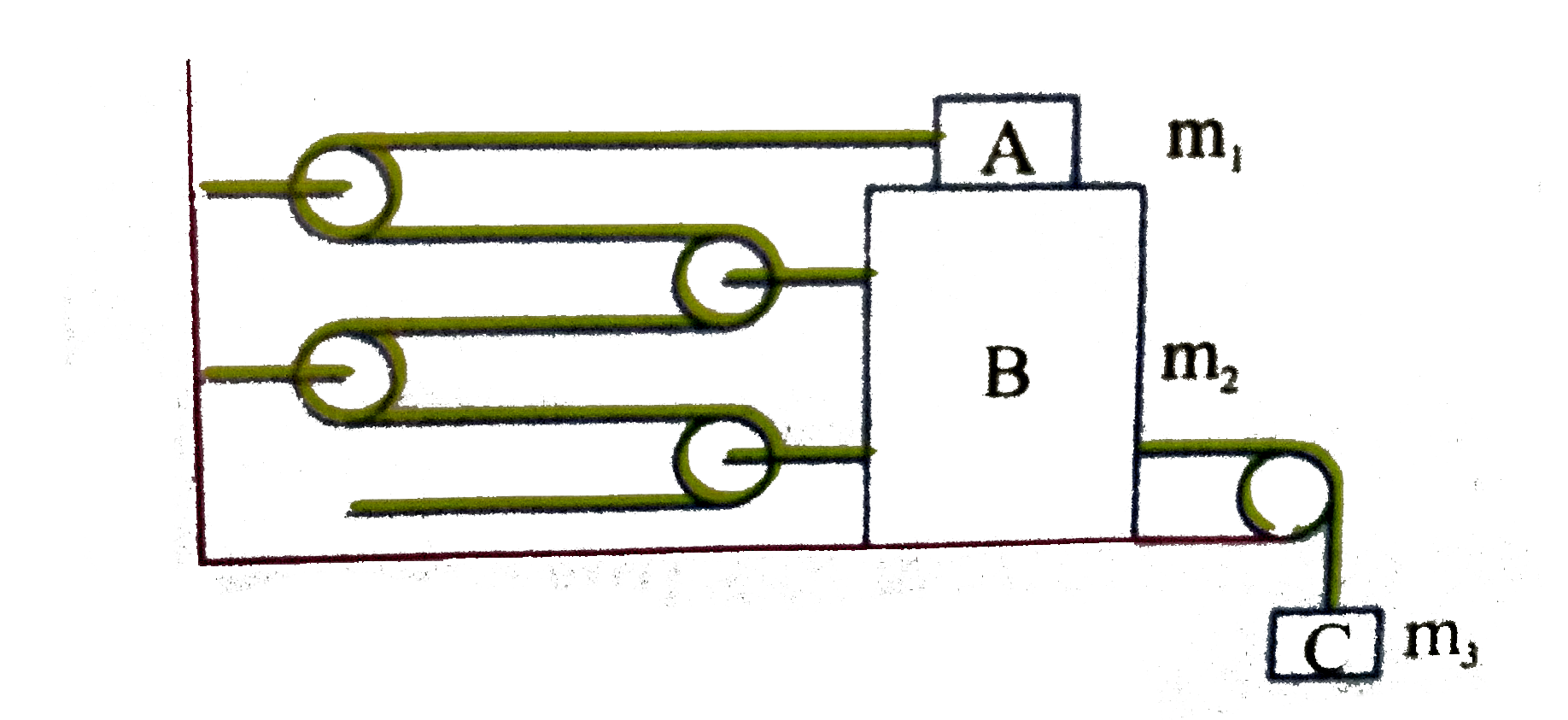 A16kgB10kgC18kgD14kg
A16kgB10kgC18kgD14kgMA=3kg,MB=4kg,MC=8kg. Coefficient of friction between any two surface is 0.25 pulley is frictionless and string is massless .A is connected to wall through a massless right rod.
 Avalue of F to keep C moving with constant speed is 80NBvalue of F to keep C moving with constant speed is 120NCif Fis200N then acceleration of B is 10m/s−2Dto slide C towards left ,F should be at least 50N (Take g=10m/s−2)
Avalue of F to keep C moving with constant speed is 80NBvalue of F to keep C moving with constant speed is 120NCif Fis200N then acceleration of B is 10m/s−2Dto slide C towards left ,F should be at least 50N (Take g=10m/s−2)
In the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionA 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
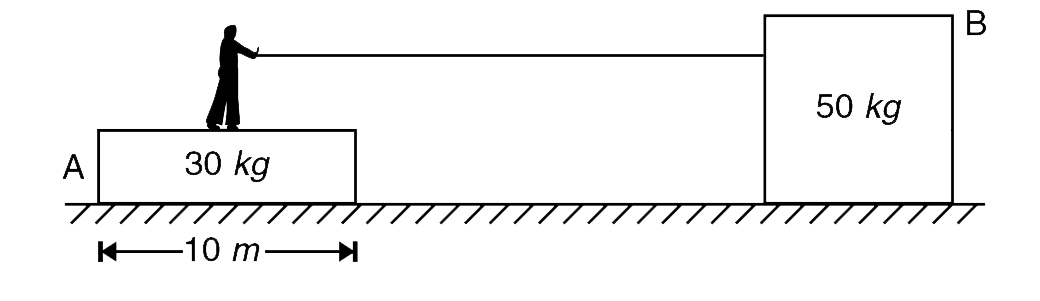
View SolutionTwo block AandB of mass mA=10kg and mA=20kg are place on rough horizontal surface . The blocks are connected with a string. If the coefficient of fraction between block A and ground is μA=0.9 and between block B and ground is μB=0.3 and the tension in the string in situation as shown in fig force 120Nand 100N start acting when the system is at rest?
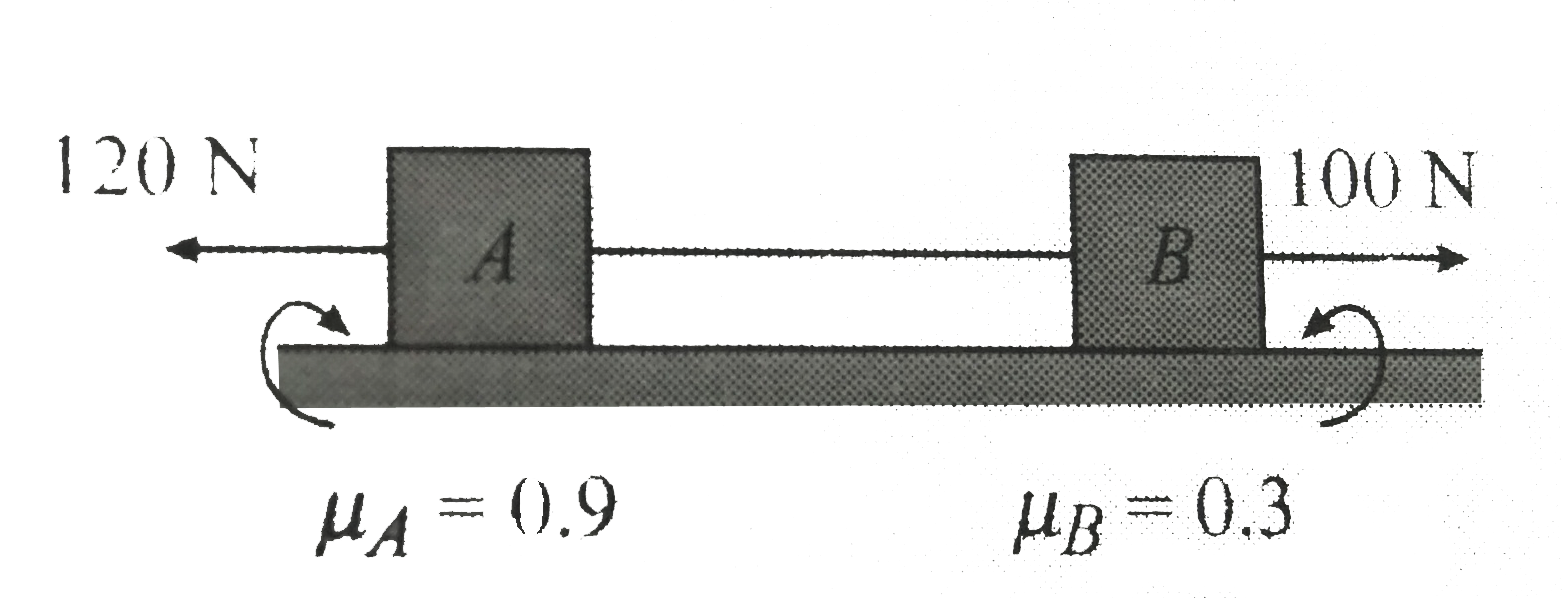
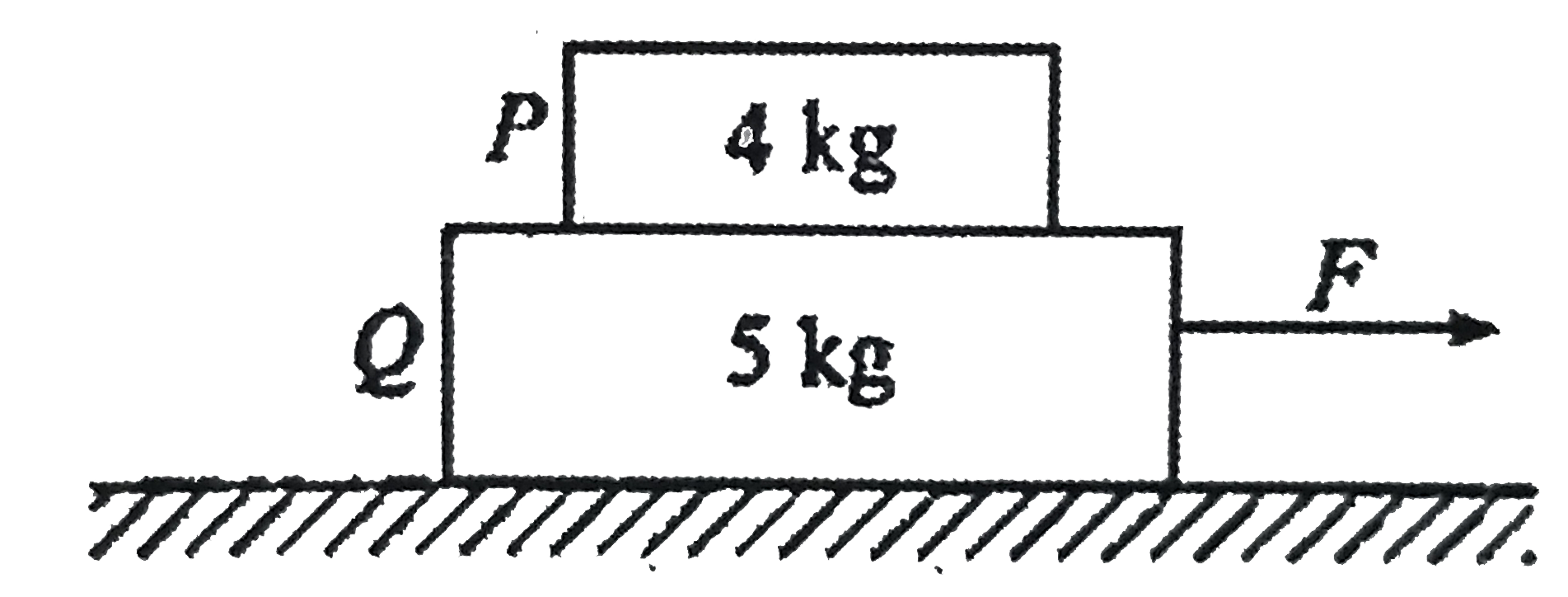
View SolutionThe coefficient of friction between 4 kg and 5 kg blocks is 0.2 and between 5 kg block and ground is 0.1 respectively. Choose the correct statement : (Take g=10m/s2)
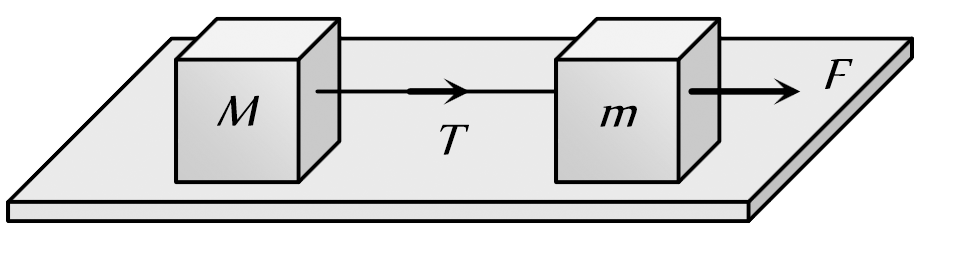
View SolutionTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
View Solution

