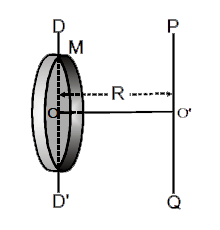
The moment of inertia of a thin sheet of mass $M$ of the given shape about the specified axis is $($ axis and sheet both are in same plane $:)$

$\frac{7}{12} M a^{2}$

$\frac{5}{12} M a^{2}$

$\frac{1}{3} M a^{2}$

$\frac{1}{12} M a^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is ( axis and sheet both are in same plane : ) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One

Find moment of inertia of a thin sheet of mass $M$ in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is $L$
A $3 M L^{2} / 8$
B $3 \sqrt{3} M L^{2} / 8$
C $7 M L^{2} / 8$
Dnone of these
Question 2 - Select One
A moment of inertia of a thin circular plate is minimum about the following axis
Aaxis perpendicular to plane of plate passing through its centre
Baxis passing through any diameter of plate
Caxis passing through any tangent of plate in its plane
Daxis passing through any tangent perpendicular to its plane
Question 3 - Select One
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
A $\frac{5}{2} I$
B $3 I$
C $\frac{3}{2} I$
D $2 I$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 58

Home
Ask Doubt
Profile

The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is ( axis and sheet both are in same plane :)

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is L

A moment of inertia of a thin circular plate is minimum about the following axis

Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 58

The moment of inertia of a thin sheet of mass $M$ of the given shape about the specified axis is $($ axis and sheet both are in same plane $:)$

Find moment of inertia of a thin sheet of mass $M$ in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is $L$