A uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
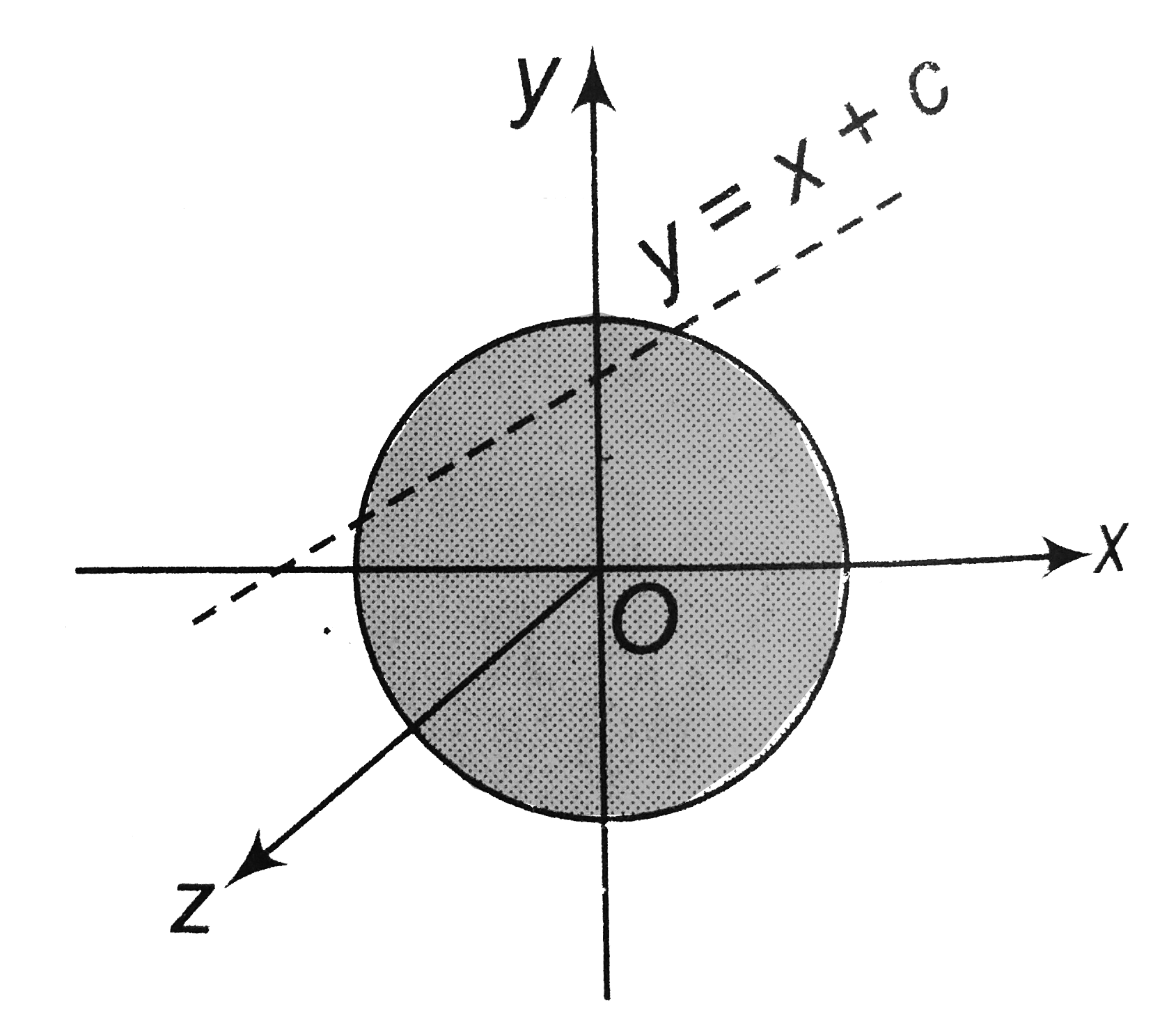 .
.
−R2
±R√2
+R4
−R
The correct Answer is:B
IPQR=IAOB+M.(ON)2
IPQR=14MR2+M.(C√2)2
But IPQR=12MR2
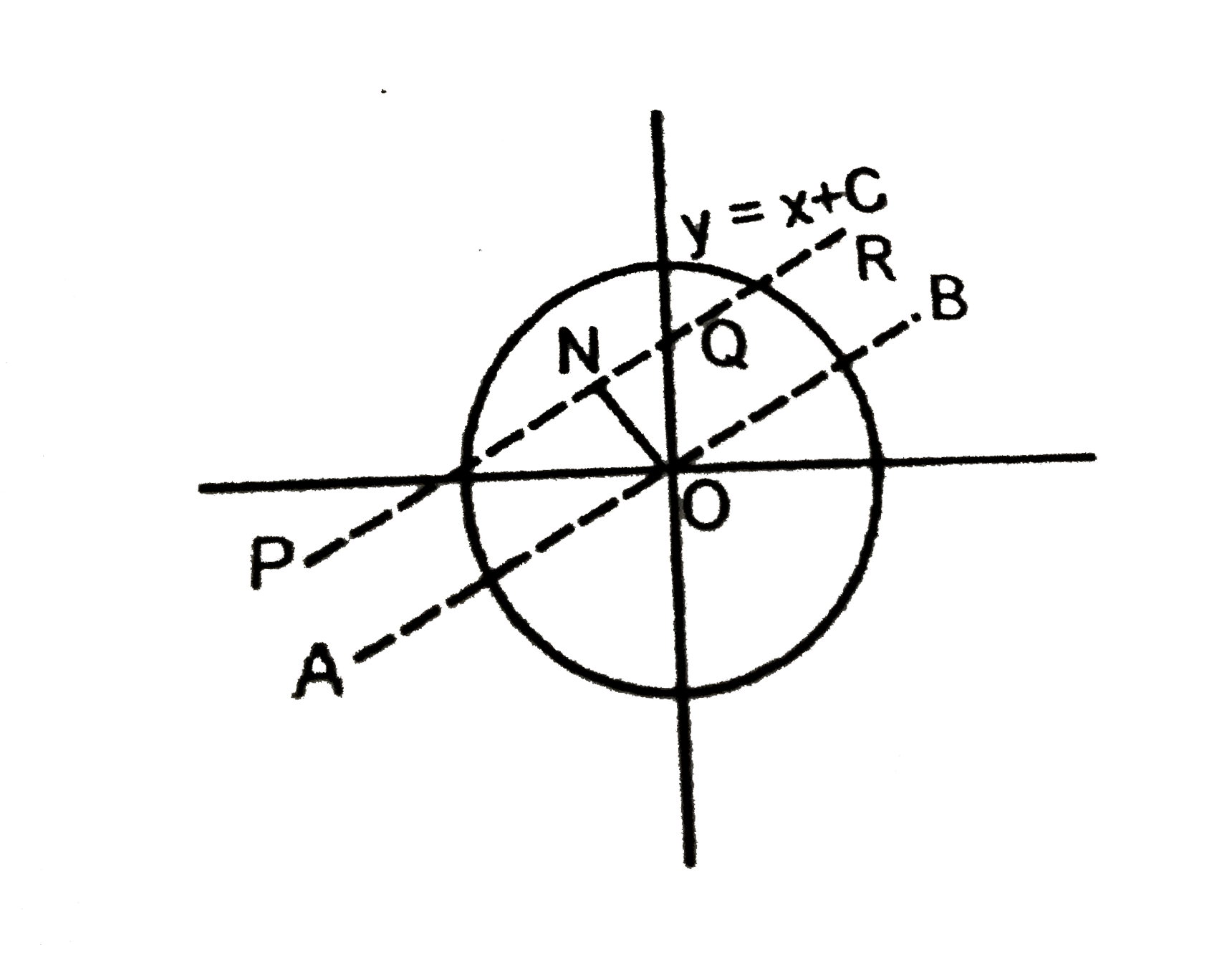
∴C=±R√2
Hence (B) is correct.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 60
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp61
Explore 6 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 58
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View Solution
Knowledge Check
A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
A43RB√172RC√13RD√152RA uniform disc of radius R lies in xy-plane with its centre at origin. Its moments of inertia about the axis X=2R and Y=0 is equal to the moment of inertia about the axis Y=d and Z=0. What is the value of d?
A√172RB√13RC√152RD43RA uniform disc of radius R lies in xy plane with its centre at origin. Its moment of inertia about the axis x = 2 R and y =0 is equal to the moment of inertia about the axis y =d and z = 0. What is d equal to ?
A√172RB√13RC√152RD43R
A rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionMoment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionA uniform circular disc of radius R lies in the XY plane with its centre coinciding with the origin.The moment of inertia about an axis passing through a point on the X-axis at a distance x=2R and perpendicular to the X-Y plane is equal to its moment of inertia about an axis passing through a pint on the Y-axis at a distance y=d and parallel to the X-axis in the X-Y plane. The value of d is
View SolutionThe moment of inertia of semicircular ring about its centre is
View Solution

