Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
MR22−M(4R3π)2
MR22−M(√24R3π)2
MR22+M(4R3π)2
MR22+M(√24R3π)2
The correct Answer is:B
To find the moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its center of mass and perpendicular to its plane, we can follow these steps:
Step 1: Understand the Moment of Inertia of a Full Disc
The moment of inertia I of a full disc about an axis through its center and perpendicular to its plane is given by the formula:
Ifull=12MR2
Step 2: Relate the Moment of Inertia of the Quarter Disc
Since we are dealing with a quarter disc, we can express the moment of inertia of the quarter disc about its center of mass. The moment of inertia of the quarter disc about the same axis can be derived from the moment of inertia of the full disc:
Iquarter=14Ifull=14(12MR2)=18MR2
Step 3: Use the Parallel Axis Theorem
To find the moment of inertia about the center of mass of the quarter disc, we can use the parallel axis theorem. The parallel axis theorem states that:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass, and d is the distance from the center of mass to the new axis.
Step 4: Calculate the Distance d
For a quarter disc, the center of mass is located at a distance d from the origin (the center of the full disc). The coordinates of the center of mass for a quarter disc can be derived, and it is found to be:
d=4R3π
Step 5: Substitute into the Parallel Axis Theorem
Now substituting d into the parallel axis theorem:
I=Iquarter+M(4R3π)2
Substituting Iquarter=18MR2:
I=18MR2+M(4R3π)2
Step 6: Simplify the Expression
Now we simplify the expression:
I=18MR2+M⋅16R29π2
Combining the terms:
I=M(18R2+16R29π2)
Step 7: Final Result
To find the final moment of inertia, we can factor out MR2:
I=MR2(18+169π2)
Conclusion
Thus, the moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its center of mass and perpendicular to its plane is:
I=MR2(18+169π2)
---
The moment of inertia I of a full disc about an axis through its center and perpendicular to its plane is given by the formula:
Ifull=12MR2
Since we are dealing with a quarter disc, we can express the moment of inertia of the quarter disc about its center of mass. The moment of inertia of the quarter disc about the same axis can be derived from the moment of inertia of the full disc:
Iquarter=14Ifull=14(12MR2)=18MR2
To find the moment of inertia about the center of mass of the quarter disc, we can use the parallel axis theorem. The parallel axis theorem states that:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass, and d is the distance from the center of mass to the new axis.
For a quarter disc, the center of mass is located at a distance d from the origin (the center of the full disc). The coordinates of the center of mass for a quarter disc can be derived, and it is found to be:
d=4R3π
Now substituting d into the parallel axis theorem:
I=Iquarter+M(4R3π)2
Substituting Iquarter=18MR2:
I=18MR2+M(4R3π)2
Now we simplify the expression:
I=18MR2+M⋅16R29π2
Combining the terms:
I=M(18R2+16R29π2)
To find the final moment of inertia, we can factor out MR2:
I=MR2(18+169π2)
Thus, the moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its center of mass and perpendicular to its plane is:
I=MR2(18+169π2)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 60
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp61
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 58
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
The moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
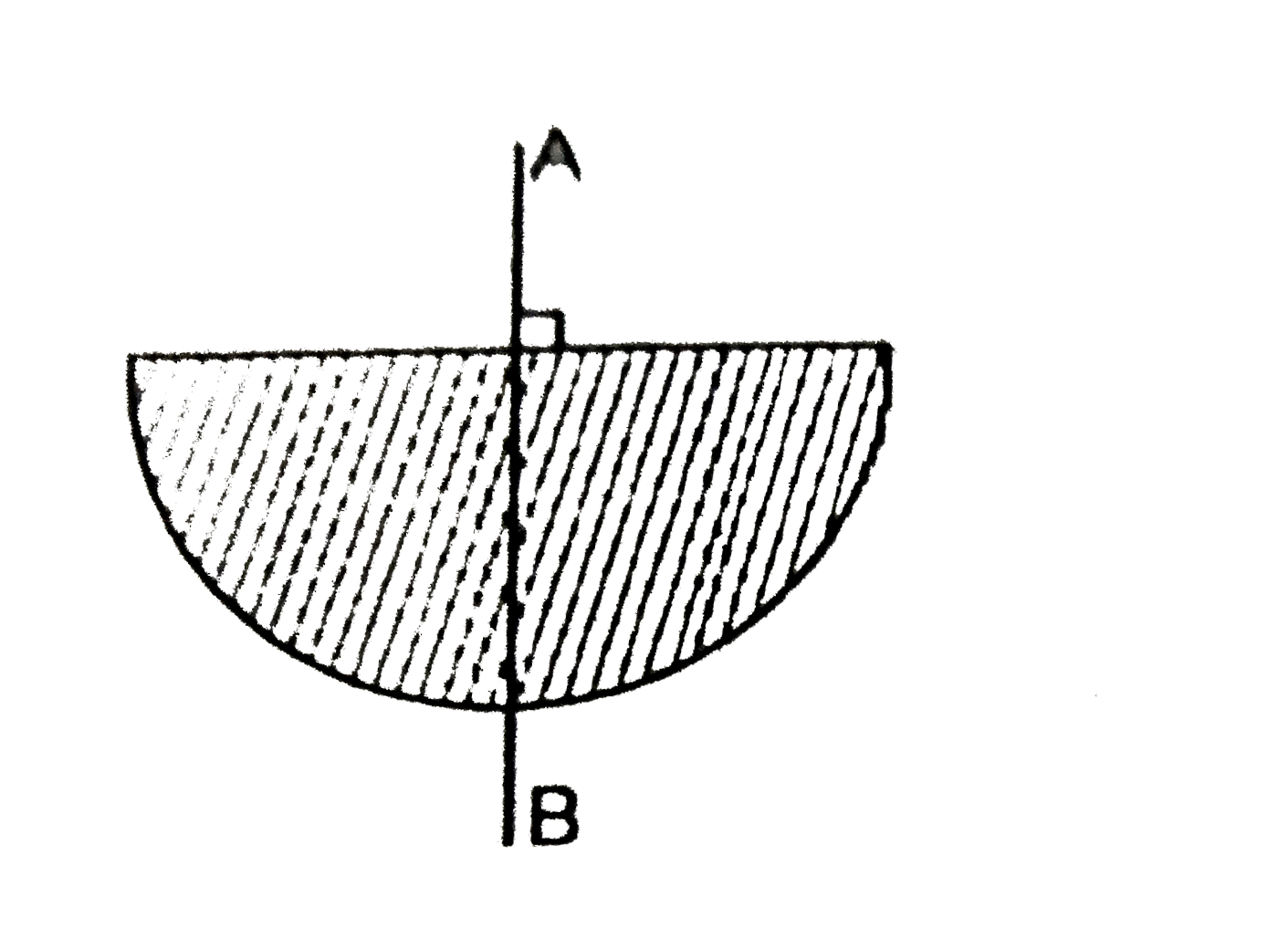 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2The moment of inertia of a cylinder of radius R, length L and mass M about an axis passing through its centre of mass and normal to its length is
AML212BMR24CM[L212+R24]DM[L212+R22]Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
ARBR2C√2RDR√2
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionThe moment of inertia of a rod of length l about an axis passing through its centre of mass and perpendicular to rod is I. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
View Solution
