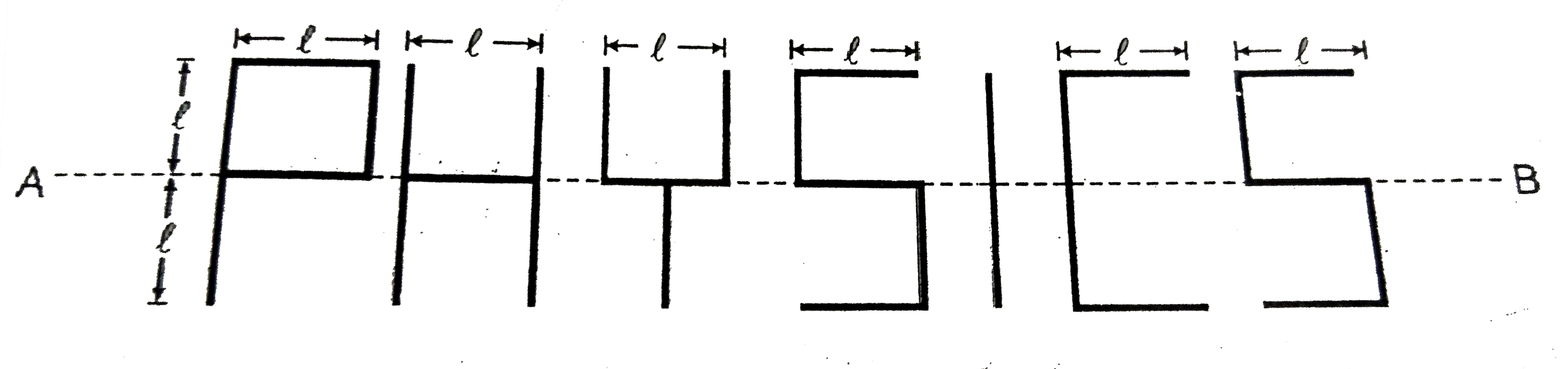
Find out the moment of inertia of the following structure ( written as PHYSICS) about axis AB made of thin uniform rods of mass per unit length λ.
Video Solution
Text Solution
The correct Answer is:13λl3
The moment of inertia of all seven rods parallel to AB and not lying on AB is
=7×(λl)l2=7λl3
the moment of inertia of all five rods lying on AB=0
The moment of inertia of all 18 rods perpendicular to AB is =18(λl)l23=6λl3
Hence net MI of rod about AB
=7λl3+6λl3=13λl3Ans.
|
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 59
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 60
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 57
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Knowledge Check
Find the M.I. of thin uniform rod of mass M and length L about the axis as shown.
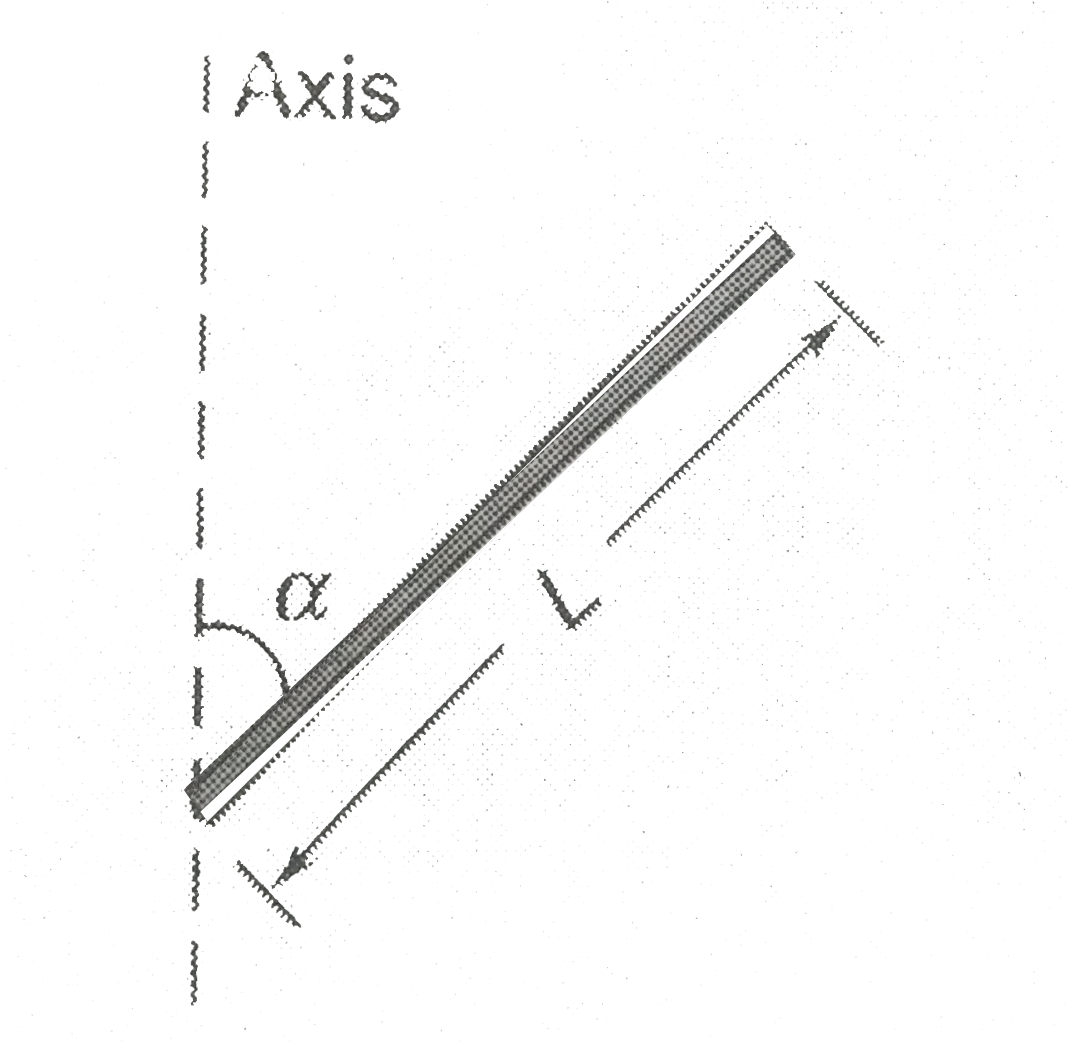 A
A B
B C
C D
D
A moment of inertia of a thin circular plate is minimum about the following axis
Aaxis perpendicular to plane of plate passing through its centreBaxis passing through any diameter of plateCaxis passing through any tangent of plate in its planeDaxis passing through any tangent perpendicular to its planeThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
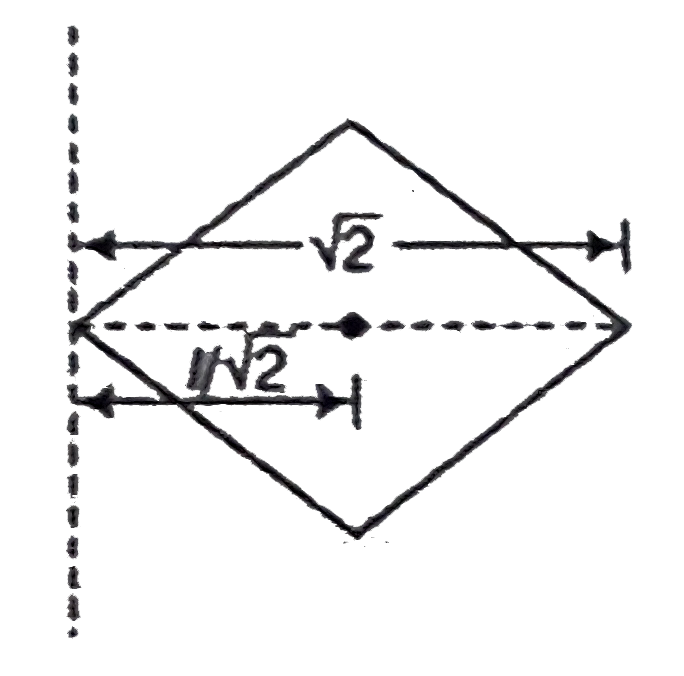 A23ml2B2ml2C3 ml2D83ml2
A23ml2B2ml2C3 ml2D83ml2
What is the moment of inertia of the thin uniform rectangular plate of mass m about the diagonal axis ×' ?

View SolutionMatch the moment of inertia of the rods with given mass and length in column A about the given axis
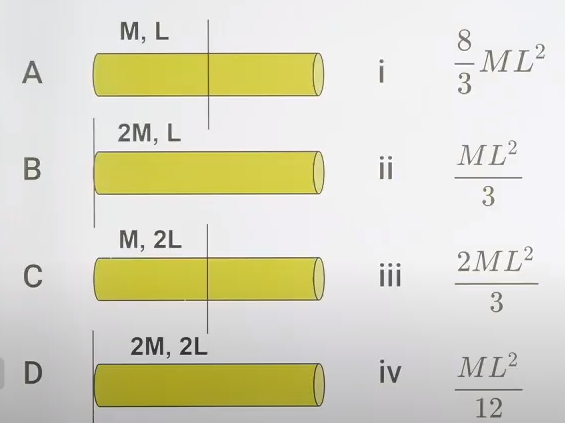
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
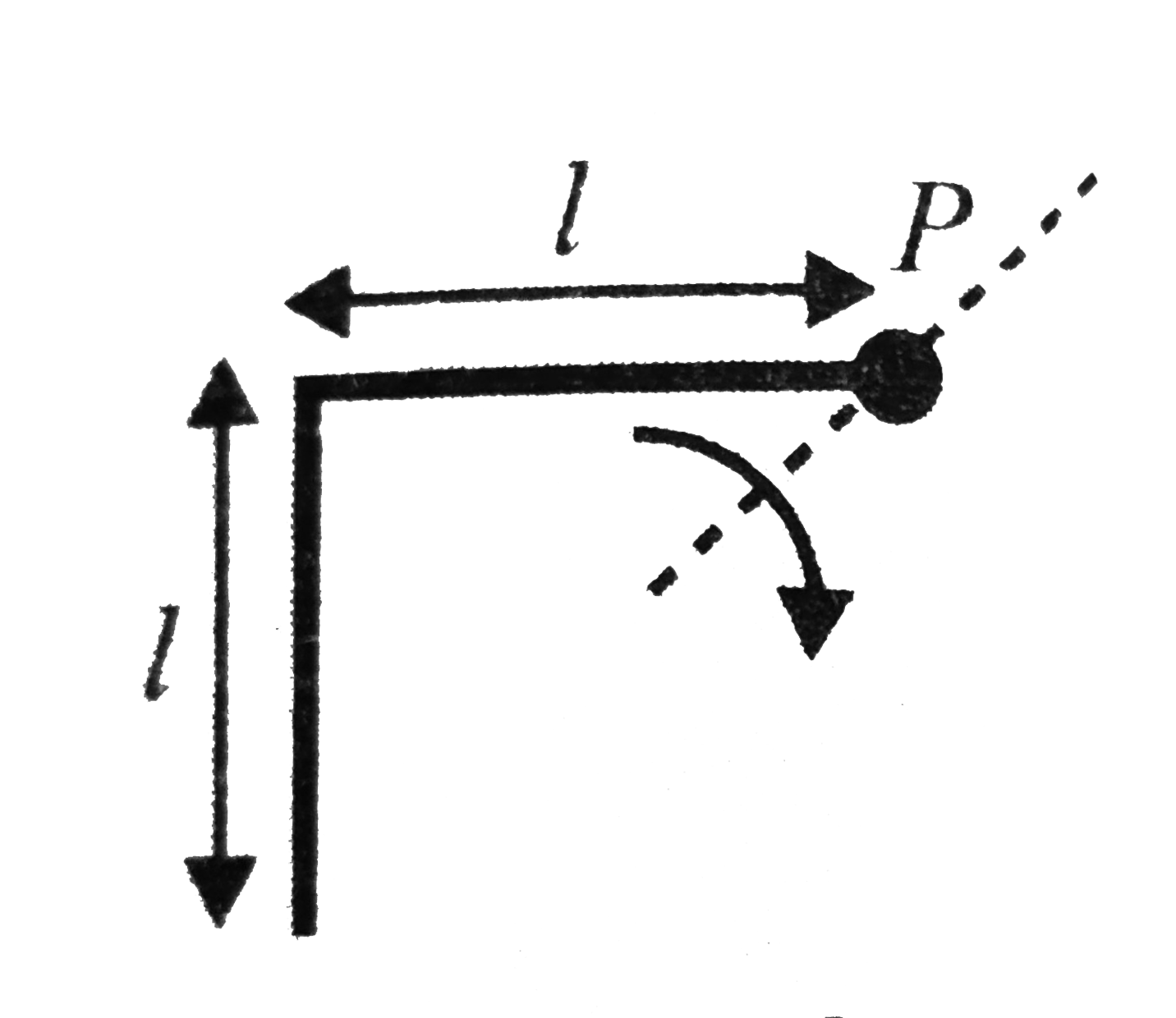
View SolutionFind the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M.
View SolutionCalculate the moment of inertia of a thin rod of mass m and length l about a symmetry axis through the centre of mass and perpendicular to the length of the rod, as shown in Fig.
View Solution


