Find the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.

Video Solution

Text Solution

Verified by Experts

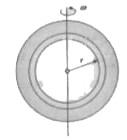
The sphere can be considered as made up of many concentric thin shells. From previous example, a spherical subshell of radius r has moment of inertia:
$d I = \frac{2}{3} d M r^{2}$ .
Calculations: We know that
$d M = \frac{M}{\frac{4}{3} π R^{3}} \times 4 π r^{2} d r$
= $\frac{3 M}{R^{3}} \times r^{2} d r$ .
Substituting for dM in the equation for moment of inertia, we get
$d I = \frac{2}{3} \times \frac{3 M}{R^{3}} r^{2} (d r) r^{2}$ .
Integrating over the whole volume, we get
$I = \frac{2 M}{R^{3}} \int_{0}^{R} r^{2} d r$
= $\frac{2 M R^{2}}{5}$ .

Updated on:21/07/2023

Find the moment of inertia of a solid sphere of mass $M$ and radias $R$ about an axis XX shown in figure.
A $\frac{7}{5} M R^{2}$
B $\frac{4}{5} M R^{2}$
C $\frac{3}{5} M R^{2}$
D $\frac{2}{5} M R^{2}$
The moment of inertia of a solid sphere of mass M and radius R about its diameter is I. The moment of inertia of the same sphere about a tangent parallel to the diameter is
A5 I
B7 I
C2.5 I
D3.5 I
Find the moment of inertia of a hemisphere of mass $M$ and radius $R$ shown in the figure, about an axis $A A'$ tangential to the hemisphere.

A $I = (\frac{9}{20}) m R^{2}$
B $I = (\frac{13}{20}) m R^{2}$
C $I = (\frac{7}{20}) m R^{2}$
D $I = (\frac{3}{20}) m R^{2}$