Three solid spheres of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
To find the potential energy of the system of three solid spheres of mass M and radius R that are in contact, we can follow these steps:
Step 1: Understand the Configuration
The three spheres are in contact with each other, and their centers form an equilateral triangle. The distance between the centers of any two spheres is equal to twice the radius R of the spheres.
Step 2: Write the Formula for Gravitational Potential Energy
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
where G is the gravitational constant.
Step 3: Calculate the Potential Energy Between Each Pair of Spheres
Since all spheres have the same mass M and the distance between the centers of any two spheres is 2R, we can calculate the potential energy for each pair:
1. Potential Energy between Sphere 1 and Sphere 2:
U12=−GMM2R=−GM22R
2. Potential Energy between Sphere 1 and Sphere 3:
U13=−GMM2R=−GM22R
3. Potential Energy between Sphere 2 and Sphere 3:
U23=−GMM2R=−GM22R
Step 4: Sum the Potential Energies
The total potential energy U of the system is the sum of the potential energies of all pairs:
U=U12+U13+U23
Substituting the values we calculated:
U=−GM22R−GM22R−GM22R
U=−3GM22R
Final Answer
Thus, the potential energy of the system of three solid spheres is:
U=−3GM22R
---
The three spheres are in contact with each other, and their centers form an equilateral triangle. The distance between the centers of any two spheres is equal to twice the radius R of the spheres.
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
where G is the gravitational constant.
Since all spheres have the same mass M and the distance between the centers of any two spheres is 2R, we can calculate the potential energy for each pair:
U12=−GMM2R=−GM22R
U13=−GMM2R=−GM22R
U23=−GMM2R=−GM22R
The total potential energy U of the system is the sum of the potential energies of all pairs:
U=U12+U13+U23
Substituting the values we calculated:
U=−GM22R−GM22R−GM22R
U=−3GM22R
Thus, the potential energy of the system of three solid spheres is:
U=−3GM22R
Similar Questions
Three solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionThree discs each of mass M and radius R are placed in contact with each other as shown in figure here. Then the MI of the system about an axis XX' is

View Solution
Knowledge Check
Three solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
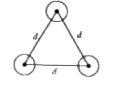 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
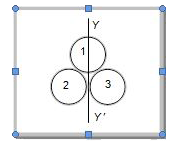 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2
Thee spheres each of mass M and radius R are placed in contact with each other as shown in the figure here. Then the moment of inertia of the system about the axis CC' is

View SolutionThree identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be

View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA system of three charges are placed as shown in the figure :
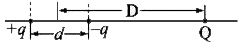
If D>>d, the potential energy of the system is :
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution
