The moment of inertia of a sphere about its diameter is I. Four such spheres are arranged as shown in figure. Find the moment of inertia of the system about the axis XX'. (radius of each sphere is 2R).

Unless explicity mentioned any sphere should be assumed to be solid.
I=25M(2R)2or, M(2R)2=52I
⇒ Isystem=I+2[I+M(2R)2]+I
=I+2I+2×52I+I=9I
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Knowledge Check
Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
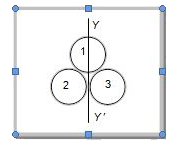 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2Moment of inertia of a solid sphere about its diameter is I . If that sphere is recast into 8 identical small spheres, then moment of inertia of such small sphere about its diameter is
AI/8BI/16CI/24DI/32Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
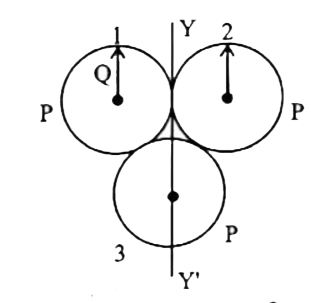 A72PQ2B27PQ2C25PQ2D52PQ2
A72PQ2B27PQ2C25PQ2D52PQ2
Four rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

View SolutionThree identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be

View SolutionThee spheres each of mass M and radius R are placed in contact with each other as shown in the figure here. Then the moment of inertia of the system about the axis CC' is

View SolutionFour spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.
View Solution

_PHY_204_Q01.png)