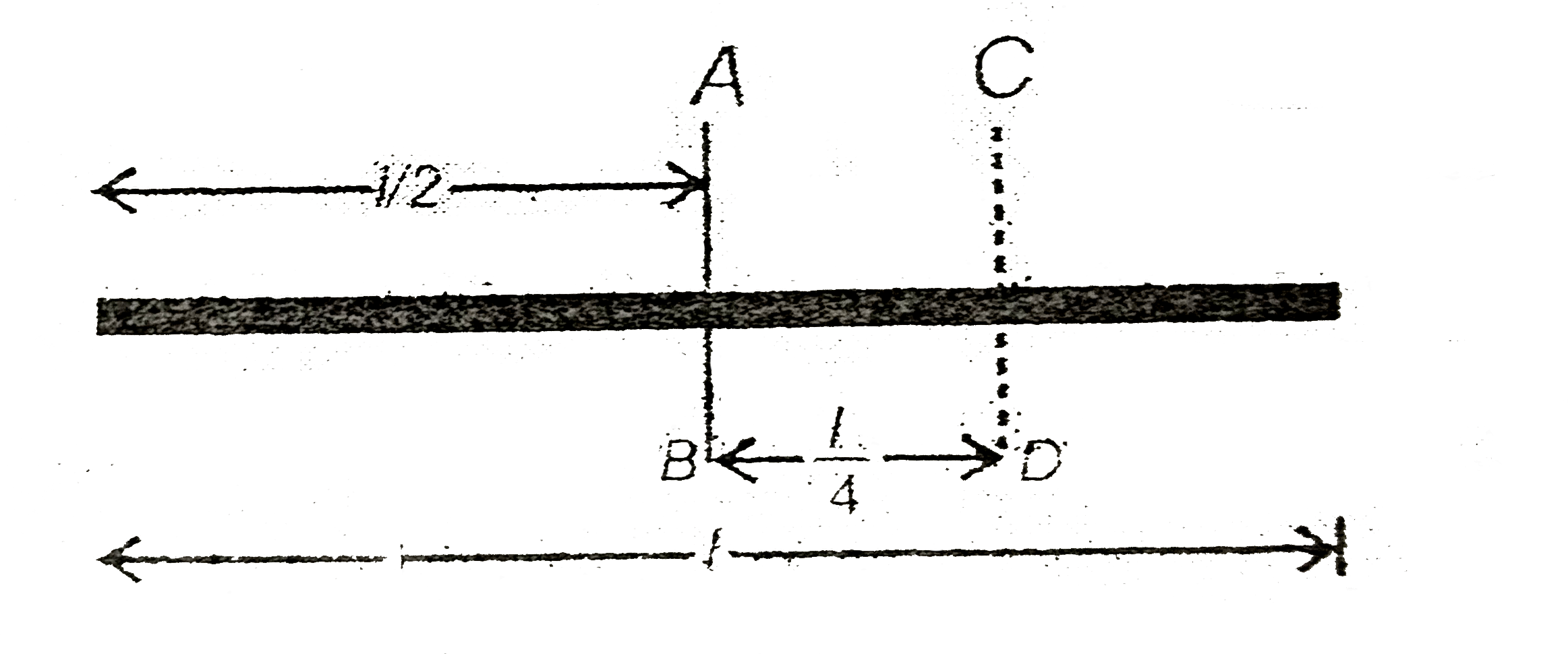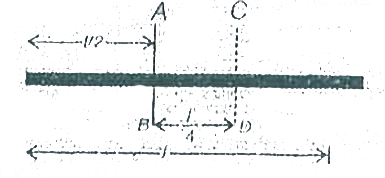Four spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.

Video Solution

Text Solution

Generated By DoubtnutGPT

To calculate the moment of inertia of the system of four spheres arranged at the corners of a square about the axis CD, we can follow these steps:
Step 1: Understand the arrangement
We have four spheres, each with mass $m$ and diameter $a$ , positioned at the corners of a square with side length $1$ . We will denote the corners as A, B, C, and D.
Step 2: Identify the axis of rotation
The axis of rotation is taken along the line CD. This means that the spheres at points C and D will have their moment of inertia calculated differently than those at points A and B.
Step 3: Calculate the moment of inertia for spheres at C and D
For spheres C and D, since the axis of rotation passes through their centers, the moment of inertia $I$ of a solid sphere about its own center is given by:
$I = \frac{2}{5} m r^{2}$
Where $r$ is the radius of the sphere. Since the diameter is $a$ , the radius $r = \frac{a}{2}$ . Thus, the moment of inertia for each sphere C and D is:
$I_{C} = I_{D} = \frac{2}{5} m {(\frac{a}{2})}^{2} = \frac{2}{5} m \frac{a^{2}}{4} = \frac{m a^{2}}{10}$
Step 4: Calculate the moment of inertia for spheres at A and B
For spheres A and B, the axis of rotation does not pass through their centers. We need to use the parallel axis theorem, which states:
$I = I_{c m} + m d^{2}$
Where $I_{c m}$ is the moment of inertia about the center of mass, and $d$ is the distance from the center of mass to the axis of rotation. The distance $d$ from the center of spheres A and B to the line CD is $\frac{1}{2}$ (since the side of the square is $1$ ).
The moment of inertia about the center of mass for spheres A and B is:
$I_{A} = I_{B} = \frac{2}{5} m {(\frac{a}{2})}^{2} = \frac{m a^{2}}{10}$
Now applying the parallel axis theorem:
$I_{A} = \frac{m a^{2}}{10} + m {(\frac{1}{2})}^{2} = \frac{m a^{2}}{10} + m \cdot \frac{1}{4} = \frac{m a^{2}}{10} + \frac{m}{4}$
$I_{B} = \frac{m a^{2}}{10} + m {(\frac{1}{2})}^{2} = \frac{m a^{2}}{10} + \frac{m}{4}$
Step 5: Total moment of inertia
Now, we can sum the moments of inertia for all four spheres:
$I_{t o t a l} = I_{C} + I_{D} + I_{A} + I_{B}$
Substituting the values:
$I_{t o t a l} = (\frac{m a^{2}}{10} + \frac{m a^{2}}{10} + (\frac{m a^{2}}{10} + \frac{m}{4}) + (\frac{m a^{2}}{10} + \frac{m}{4}))$
Combining the terms:
$I_{t o t a l} = \frac{2 m a^{2}}{10} + 2 (\frac{m a^{2}}{10} + \frac{m}{4})$
$I_{t o t a l} = \frac{2 m a^{2}}{10} + \frac{2 m a^{2}}{10} + \frac{m}{2} = \frac{4 m a^{2}}{10} + \frac{m}{2}$
$I_{t o t a l} = \frac{2 m a^{2}}{5} + \frac{m}{2}$
Final Result
Thus, the moment of inertia of the system about the axis CD is:
$I_{t o t a l} = \frac{2 m a^{2}}{5} + \frac{m}{2}$

Updated on:18/9/2024

Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then the moment of inertia of the system about an axis along one of the sides of the square is
A $\frac{4}{5} M a^{2} + 2 M b^{2}$
B $\frac{8}{5} M a^{2} + 2 M b^{2}$
C $\frac{8}{5} M a^{2} + M b^{2}$
D $\frac{4}{5} M a^{2} + 4 M b^{2}$
Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
A $M a^{2} + 2 M b^{2}$
B $M a^{2}$
C $M a^{2} + 4 M b^{2}$
D $\frac{8}{5} M a^{2} + 2 M b^{2}$
Four particles each of mass $m$ are placed at the corners of a square of side length $l$ . The radius of gyration of the system about an axis perpendicular to the plane of square and passing through its centre is
A $\frac{5}{2} M (4 r^{2} + 5 R^{2})$
B $\frac{2}{5} M (4 r^{2} + 5 R^{2})$
C $\frac{2}{5} M (4 r^{2} + 5 r^{2})$
D $\frac{5}{2} M (4 r^{2} + 5 r^{2})$