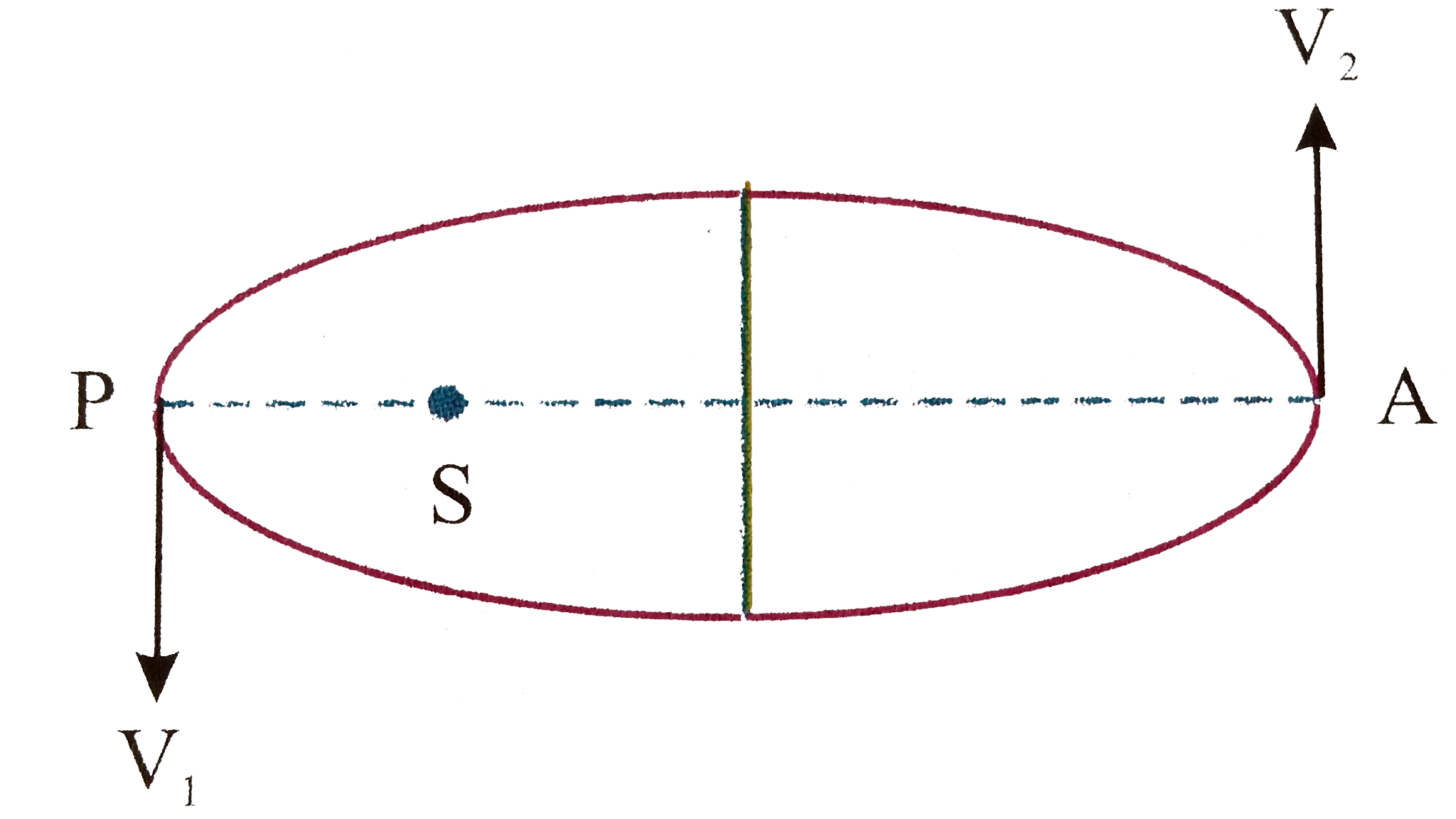
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
√GMa(1+e)(1−e)
1+e1−e√GMa
√GMa3(1+e)(1−e)
√GMa3(1+e2)(1−e2)
The correct Answer is:A

From angular momentum conservation
mvp×rp=mvArA⇒vpvA=rArp=87507000=1.25
from conservation,
mv2p2−GMemrp=mv2A2−GMemrA
⇒v2A−v2p=GMe(1rA−1rp)
⇒vA=4.51km/s and vp=5.64km/s
Also length of semi-major axis is rA+rP
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Find the speeds of a planet of mass m in its perihelion and aphelion postitions. The semimajor axis of its orbit is a, ecentricity is e and te mass of the sun is M. Also find the total energy of the planet in terms of the given parameters.
View SolutionThe areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to
View Solution
Knowledge Check
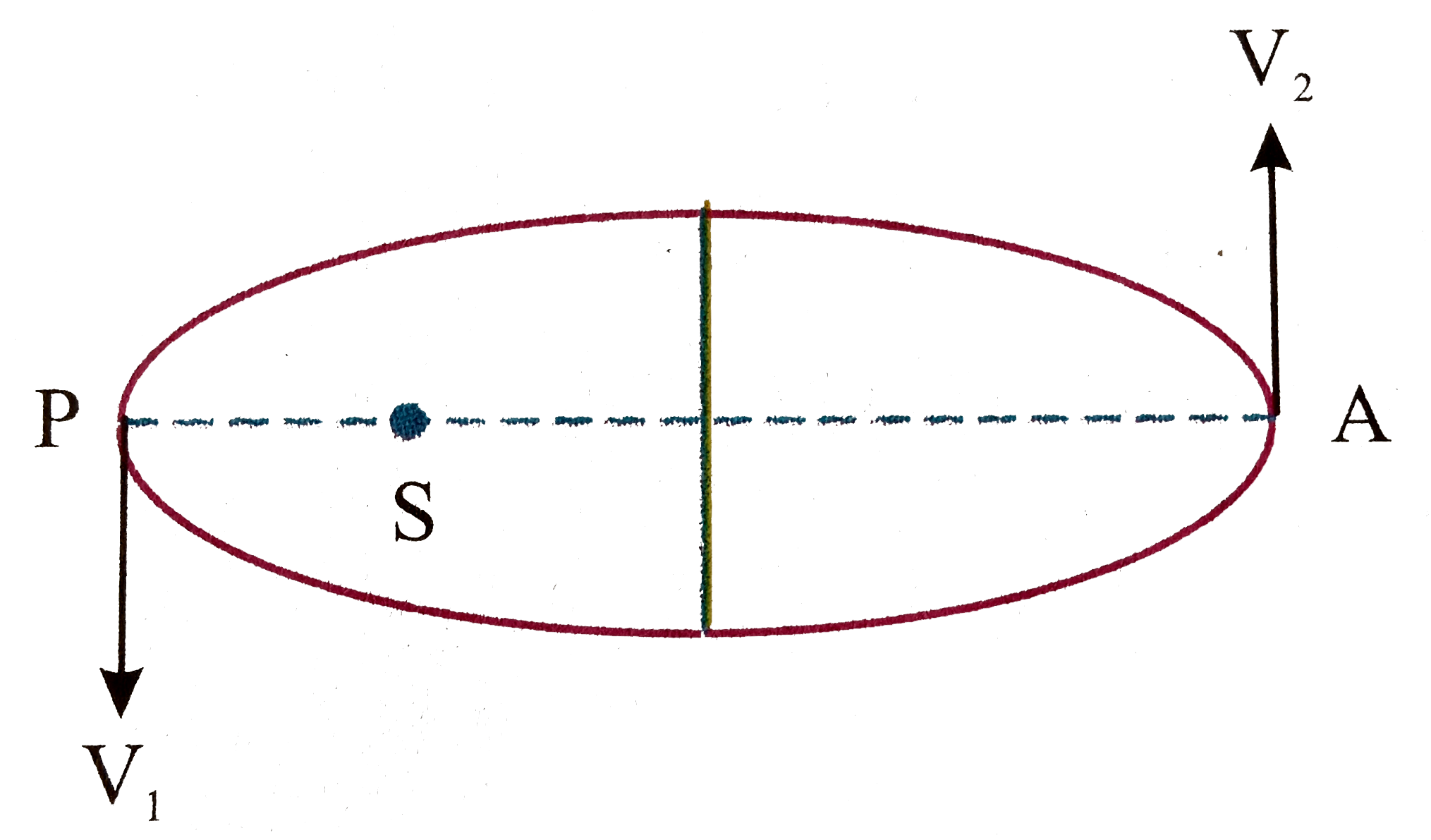
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.A√GMa(1+e)(1−e)B√GMa(1−e)(1+e)C√GMa3(1+e2)(1−e2)D√GMa3(1−e2)(1+e2)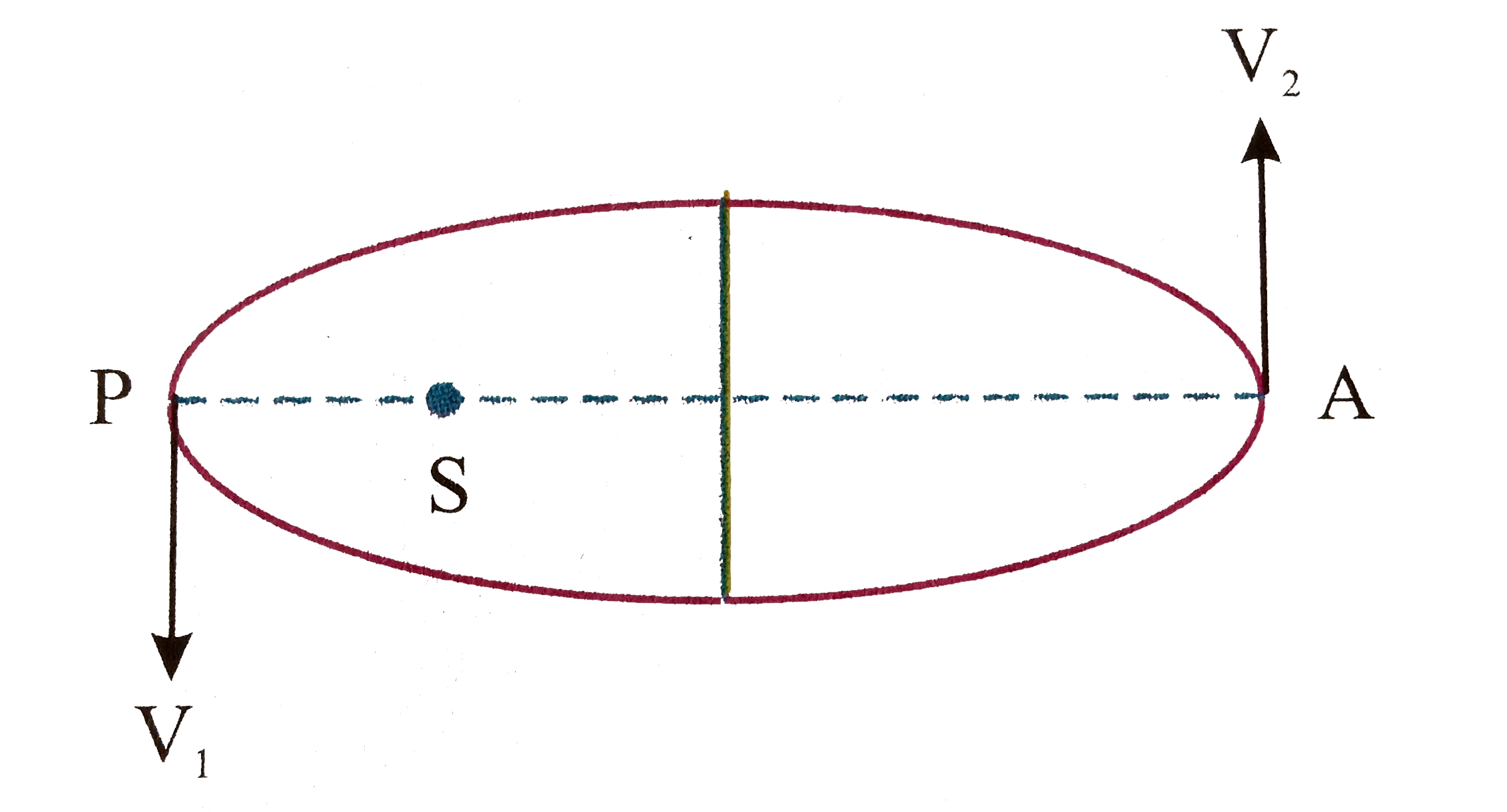
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.A−GMm4aB−GMm22aC−GMm8aD−GMm2aA planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusion
A planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b , then the time period is given by :
View SolutionA planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionA hypothetical planet of mass m is moving along an elliptical path around sun of mass Ms under the influence of its gravitational pull. If the major axis is 2R, find the speed of the planet when it is at a distance of R from the sun.
View SolutionA planet of mass m is in an elliptical orbit about the sun with an orbital period T. If A be the area of orbit, then its angular momentum would be
View SolutionA plantet is moving round the sun in an elliptical orbit as shows. As the planet moves from a to B
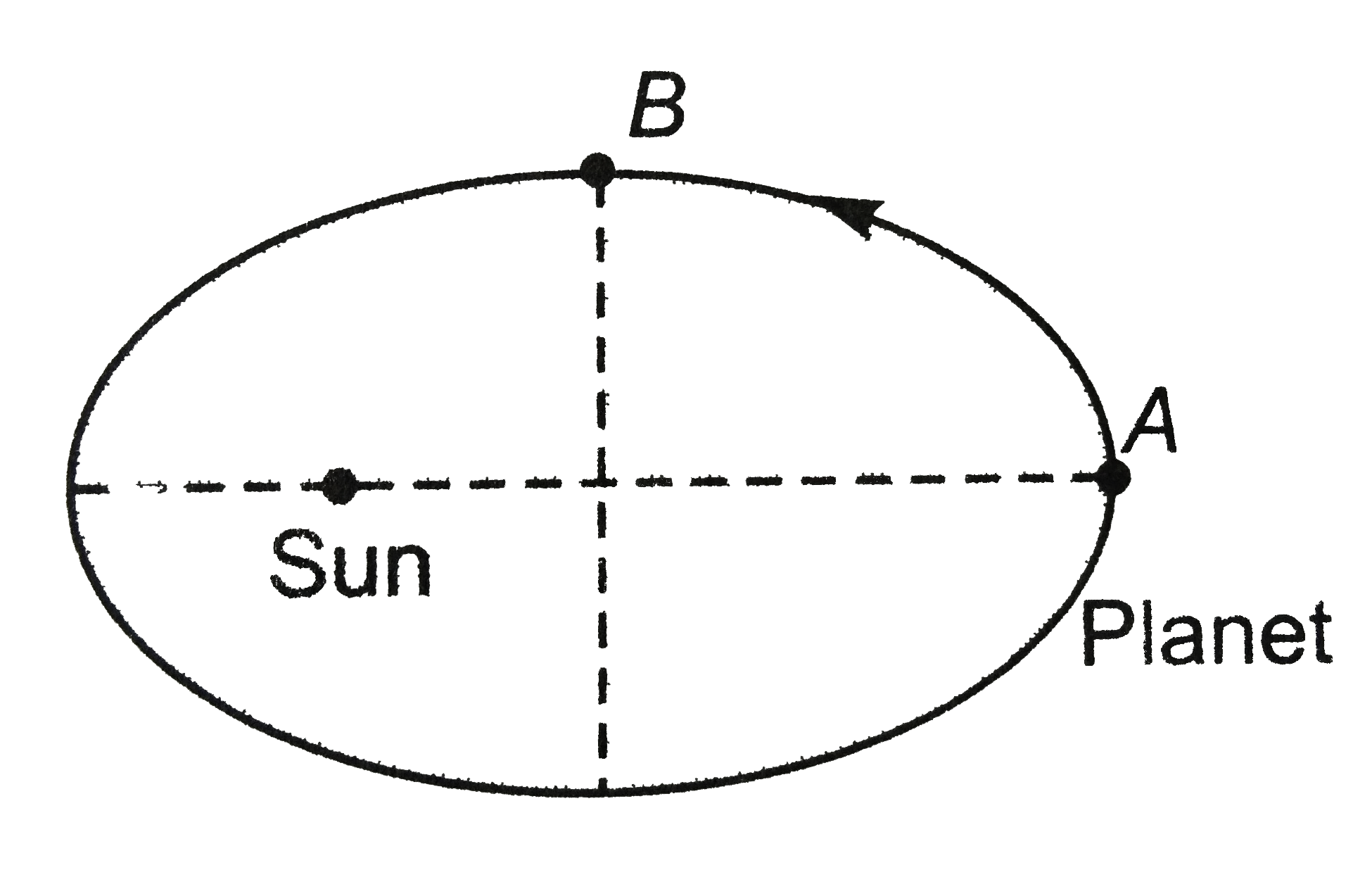
View Solution

