A planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b , then the time period is given by :
T2∝b3
T2∝(a+b2)3
T2∝a3
T2∝(a−b2)3
The correct Answer is:C
To find the time period of a planet revolving in an elliptical orbit around the sun, we can use Kepler's Third Law of Planetary Motion. The law states that the square of the time period (T) of a planet is directly proportional to the cube of the semi-major axis (a) of its orbit.
1. Understanding Kepler's Third Law:
Kepler's Third Law states that for any planet orbiting the sun, the square of its orbital period (T) is proportional to the cube of the semi-major axis (a) of its elliptical orbit. Mathematically, this can be expressed as:
T2∝a3
2. Expressing the Proportionality:
To convert the proportionality into an equation, we introduce a constant of proportionality (k):
T2=k⋅a3
3. Identifying the Constant:
The constant k depends on the mass of the sun and the gravitational constant (G). For our purposes, we can state that:
k=4π2G(M+m)
where M is the mass of the sun and m is the mass of the planet. However, since the mass of the planet is negligible compared to the mass of the sun, we can simplify this to:
k≈4π2GM
4. Final Expression for the Time Period:
Substituting this back into our equation, we get:
T2=4π2GMa3
Therefore, the time period T can be expressed as:
T=2π√a3GM
5. Conclusion:
Thus, the time period of a planet revolving in an elliptical orbit around the sun, with semi-major axis a, is given by:
T2∝a3
Kepler's Third Law states that for any planet orbiting the sun, the square of its orbital period (T) is proportional to the cube of the semi-major axis (a) of its elliptical orbit. Mathematically, this can be expressed as:
T2∝a3
To convert the proportionality into an equation, we introduce a constant of proportionality (k):
T2=k⋅a3
The constant k depends on the mass of the sun and the gravitational constant (G). For our purposes, we can state that:
k=4π2G(M+m)
where M is the mass of the sun and m is the mass of the planet. However, since the mass of the planet is negligible compared to the mass of the sun, we can simplify this to:
k≈4π2GM
Substituting this back into our equation, we get:
T2=4π2GMa3
Therefore, the time period T can be expressed as:
T=2π√a3GM
Thus, the time period of a planet revolving in an elliptical orbit around the sun, with semi-major axis a, is given by:
T2∝a3
Topper's Solved these Questions
- GRAVITATIONBook:PHYSICS WALLAHChapter:GRAVITATIONExercise:Level- 2
Explore 30 Videos
- GRAVITATIONBook:PHYSICS WALLAHChapter:GRAVITATIONExercise:NEET Past 5 Years Questions
Explore 13 Videos
- GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSBook:PHYSICS WALLAHChapter:GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSExercise:NEET Past 5 Years Questions
Explore 14 Videos
- KINETIC THEORY Book:PHYSICS WALLAHChapter:KINETIC THEORY Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 11 Videos
Similar Questions
A planet revolves in an ellipticle orbit around the sun. the semimjor and semiminor axis are a and b. How time-period is related with them?
View SolutionIn the figure shown a planet moves in an elliptical orbit around the sun. Compare the speeds, linear and angular momenta at the points A and B.
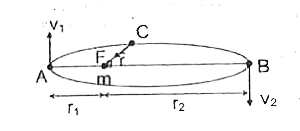
View Solution
Knowledge Check
A planet revolves round the sun in an elliptical orbit of semi minor and semi major axes x and y respectively. Then the time period of revolution is proportional to
A(x+y)32B(y−x)32Cx32Dy32A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 AABBCCDD
AABBCCDDA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
For a planet revolving around sun, if a and b are the respective semi-major and semi-minor axes, then the square of its time period is proportional to
View Solution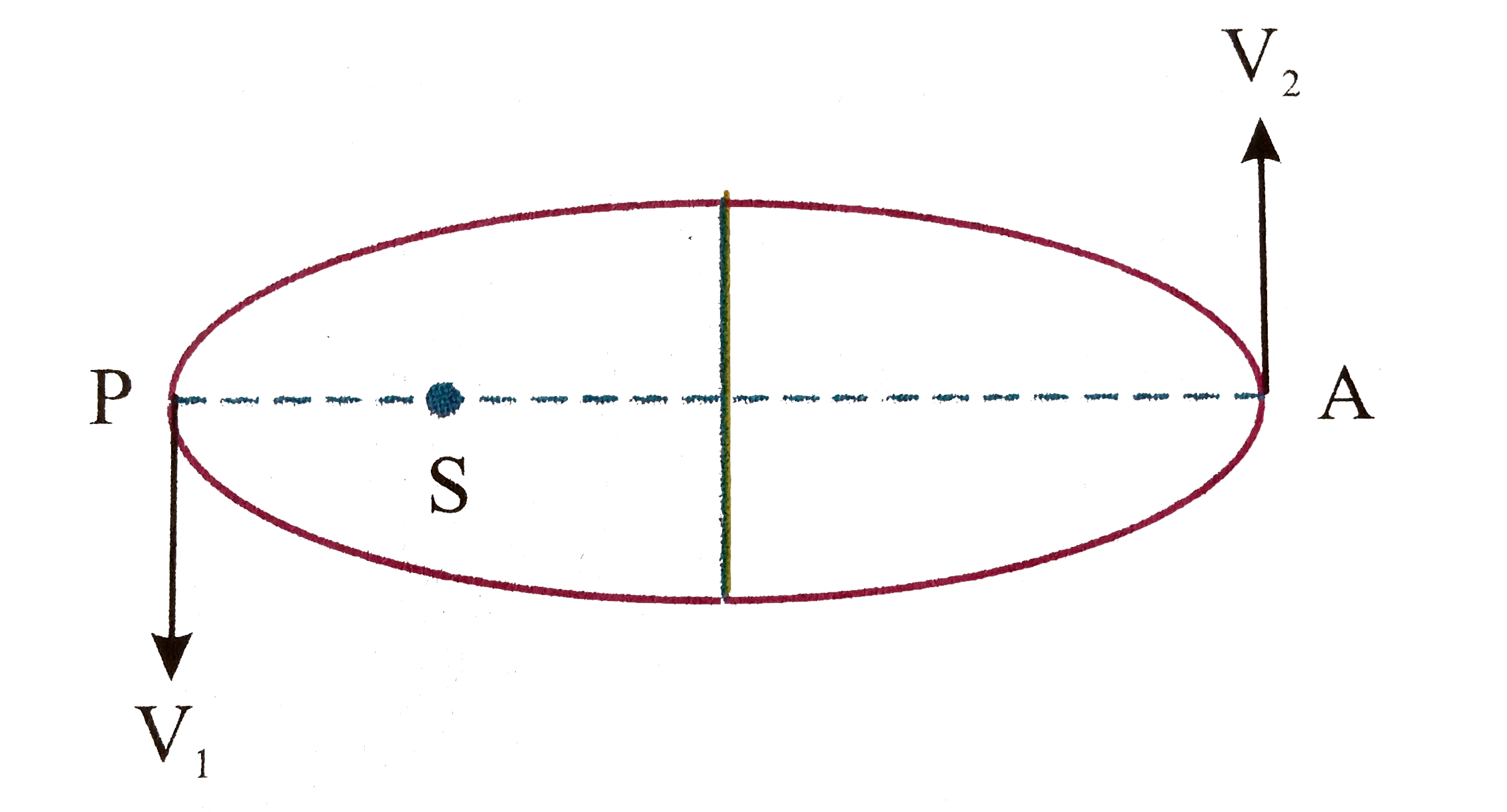
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
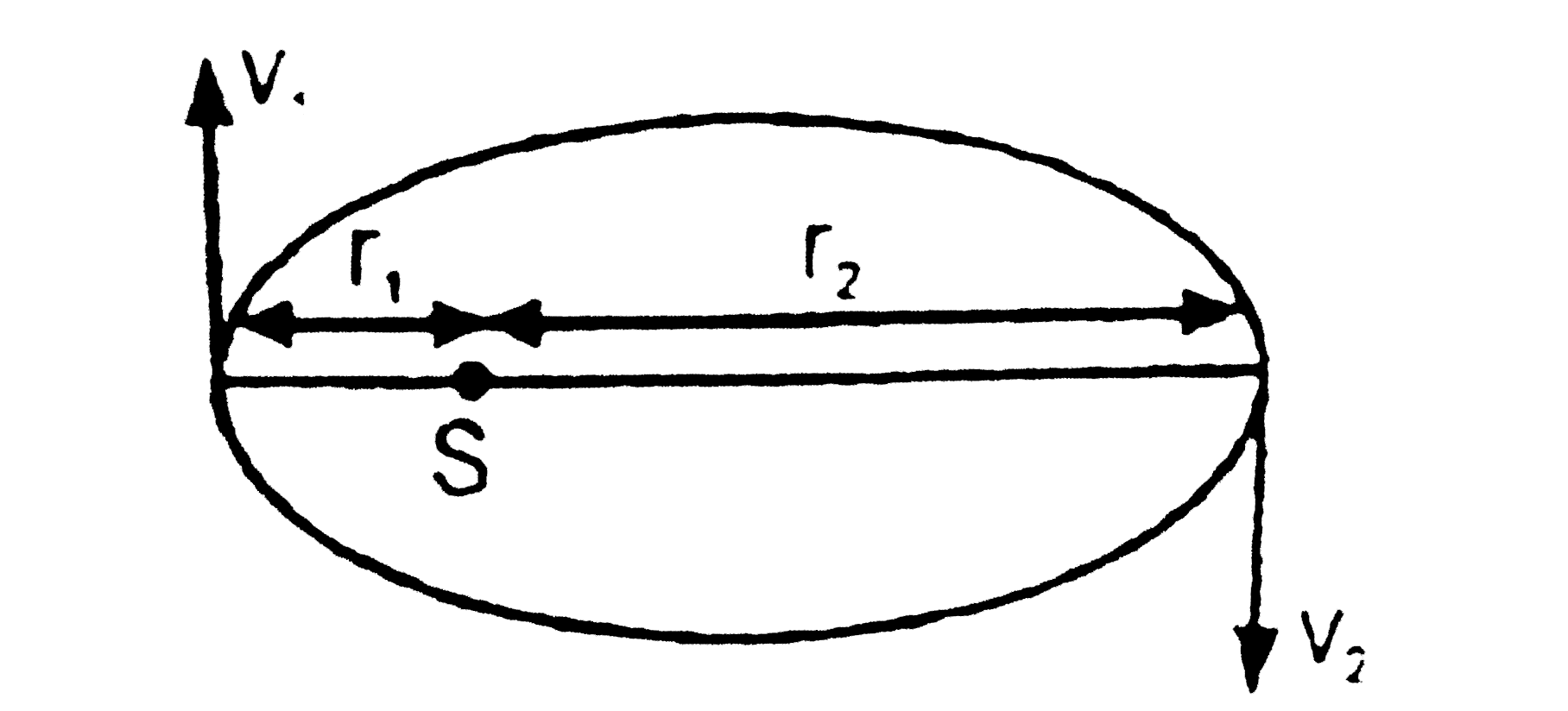
View Solution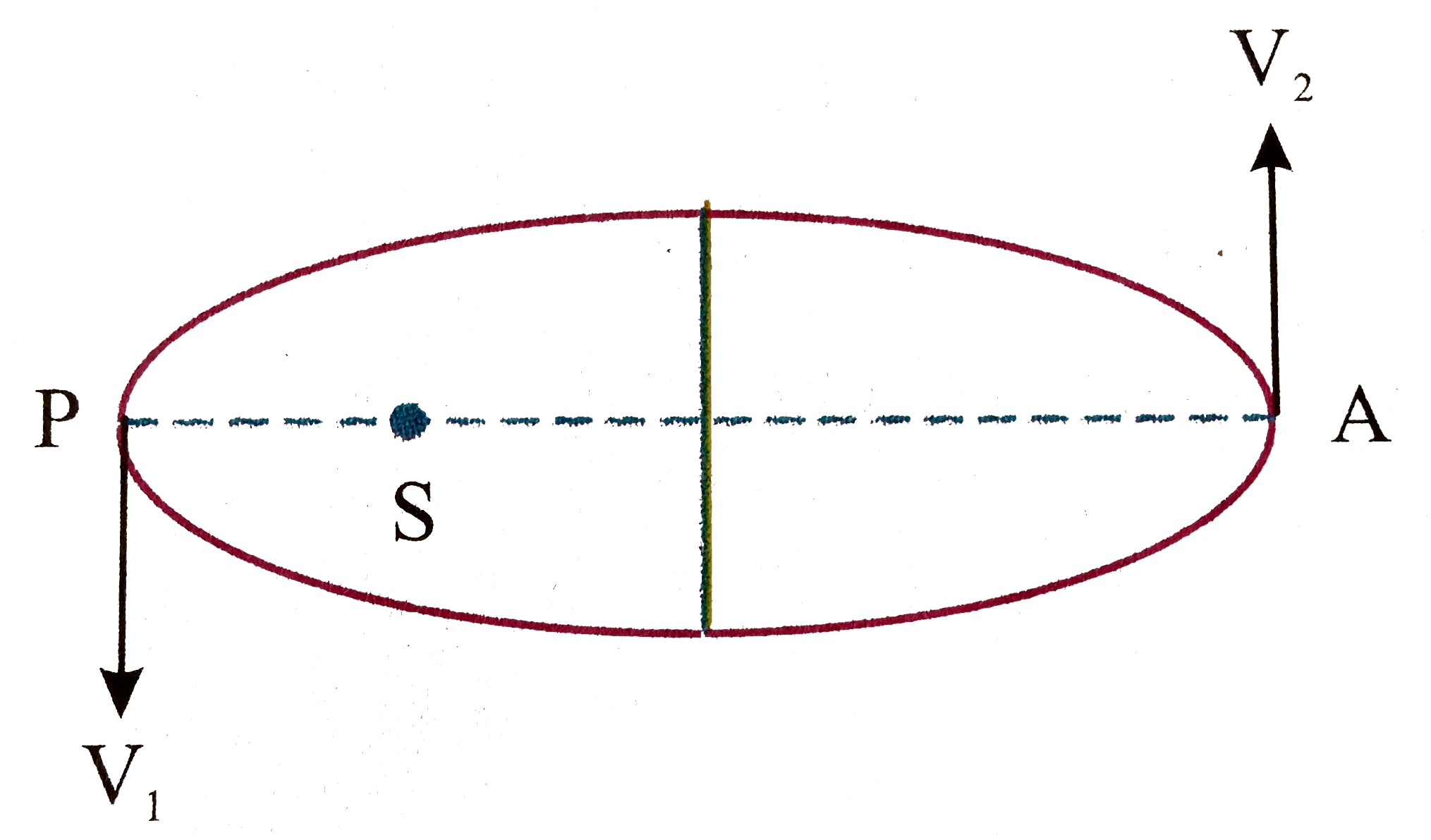
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.
View Solution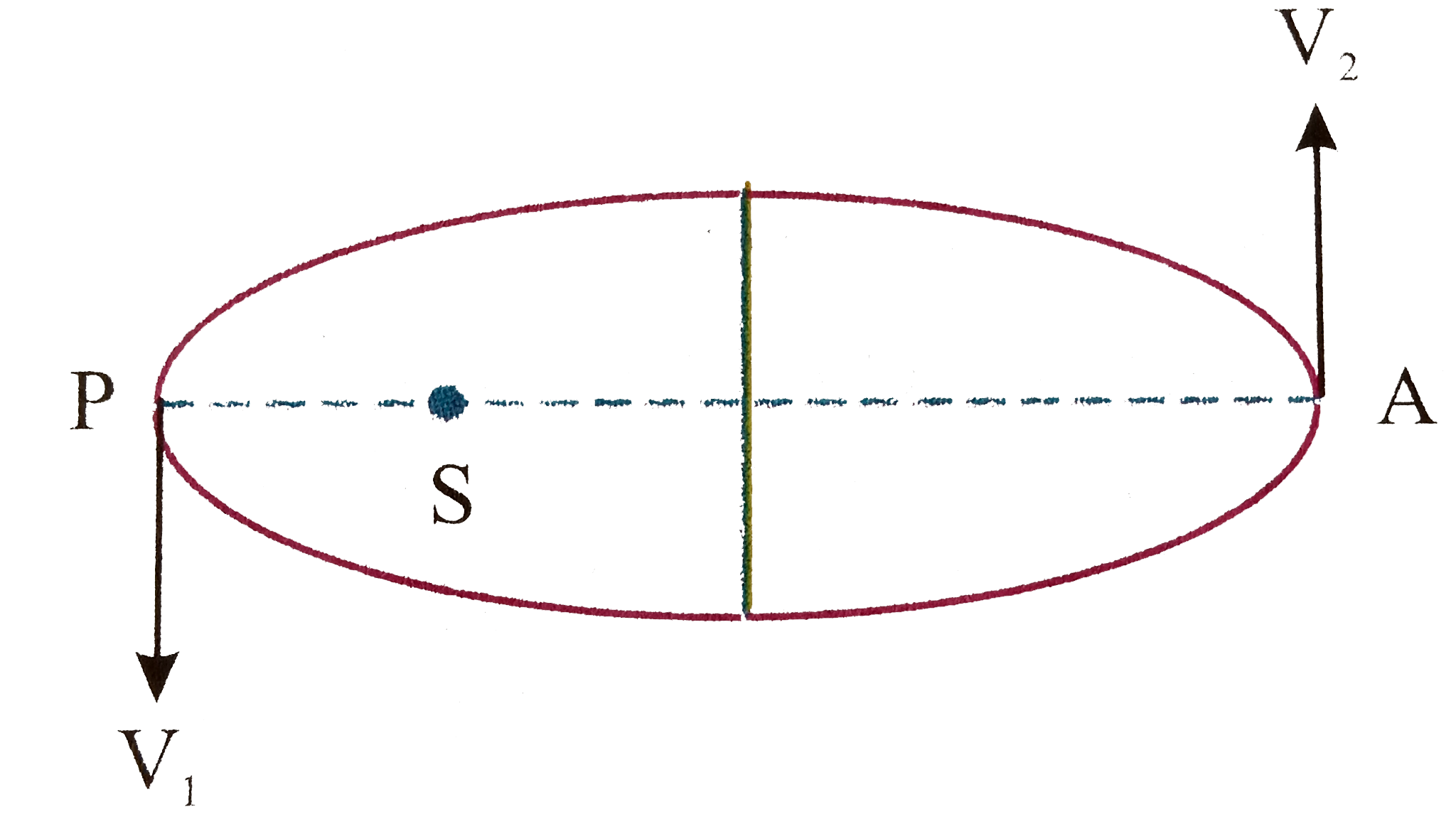
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
View Solution