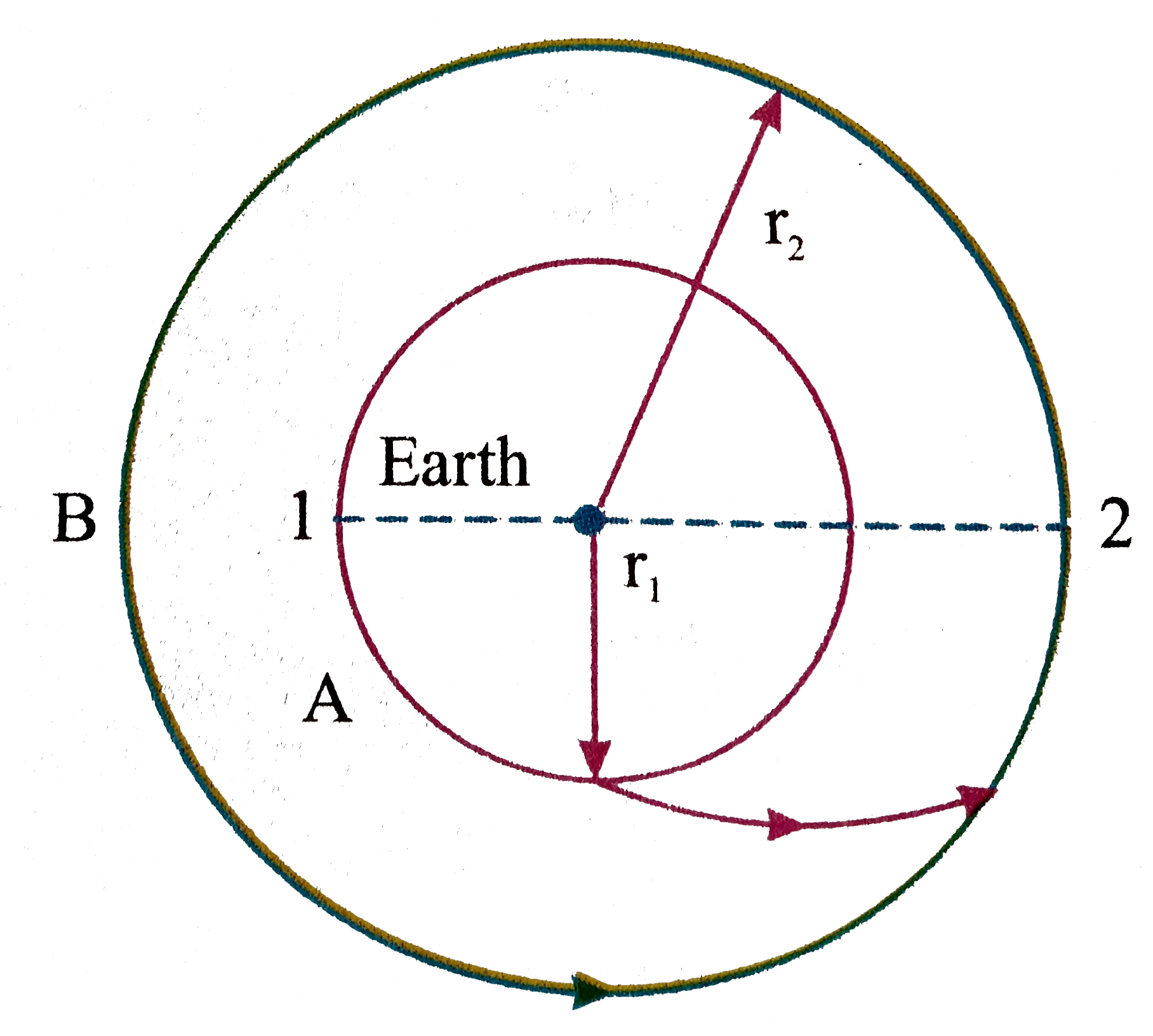
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If the two have same mass
A would have more potential energy than B while on their initial circular paths
A would have more kinetic energy than B while on their initial circular paths
Relative to earth's centre, angular momentum of A when it is in elliptical path would be less than angular momentum of B
During the whole process angular momentum of B would be more than angular momentum of A
The correct Answer is:B, C
Acceleration due to gravity near the surface of shell can be assumed to be uniform (h<<R)
g=G(2M)(2R)2=GM2R2 from h=12gt2
t=√2hg=2√hR2GM
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION
49 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EVALUATE YOURSELF -1
3 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-V
54 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Two satellites of mass MA and MB are revolving around a planet of mass M in radius RA and RB respectively. Then?
View SolutionTwo stars of masses m1 and m2 form a binary system,revolving around each other in circular orbits of radii r1 and r2 respectively.Time period of revolution for this system is

View Solution
Knowledge Check
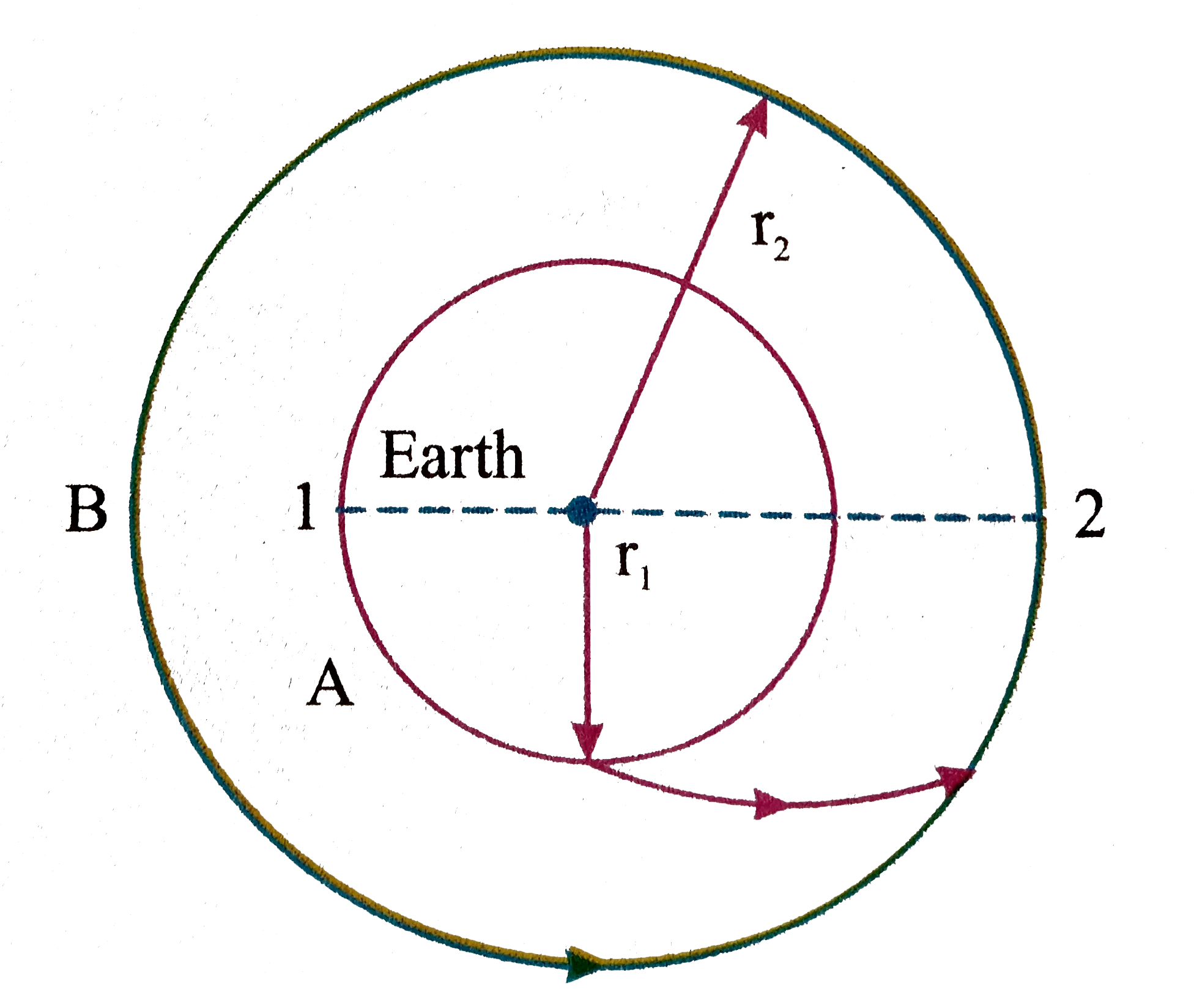
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
When A is given its first impulse at that momentAA,B and the earth centre are in same straight lineBB is a head of A angularlyCB is behind of A angularlyDnone of the above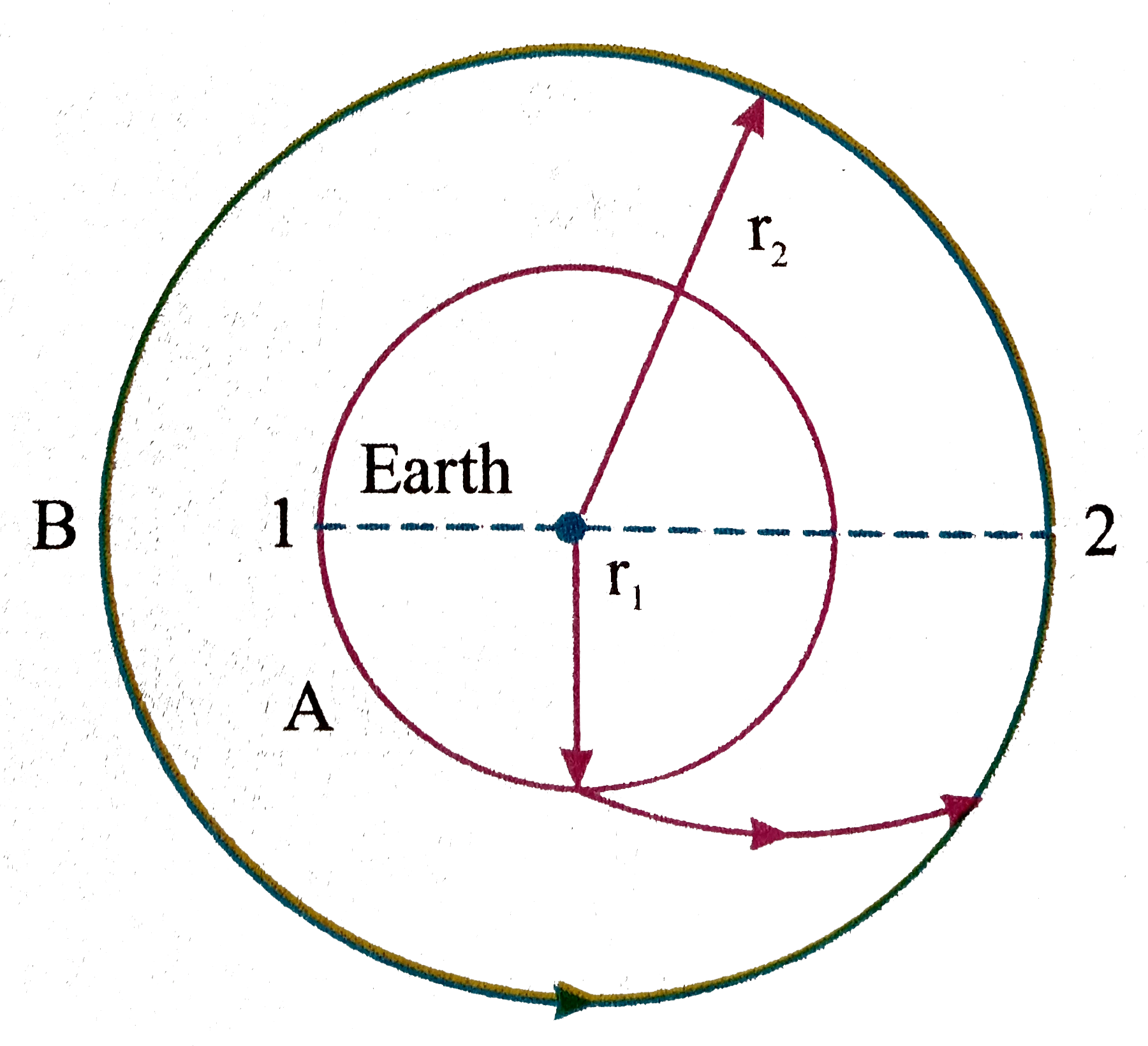
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T then time taken by A in moving from position 1 to position 2 isAT√3√2BT√32CT√23√3DT√23Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.

For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If the two have same massAA would have more potential energy than B while on their B while on their initial circular paths.BA would have more kinetic energy than B while on their initial circular paths.CRelative to Earth's centre, angular momentume of A when it is in elliptical path would be less than angular momentum of B.DDuring the whole process angular of B T than taken by A in moving from position 1 to position 2
Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.
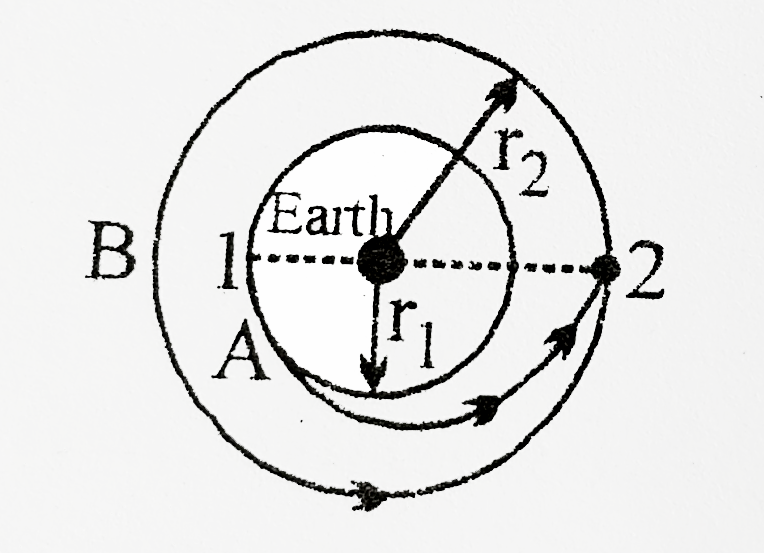
For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T than time taken by A in moving from position 1 to position 2
View SolutionTwo satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.

For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
When A is given its first impulse at the moment.
View SolutionSatellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is-
View SolutionA satellite revolves around the earth in an elliptical orbit. Its speed is
View SolutionTwo satellite are revolving around the earth with velocities v1 and v2 and in radii r1 and r2(r1>r2) respectively. Then
View Solution
