A spherical hollow is made in a lead sphere of radius R such that its surface touches the outside surface of the lead sphere and passes through the centre. The mass of the lead sphere before hollowing was M. The force of attraction that this sphere would exert on a particle of mass m which lies at a distance d from the centre joining the centre of the sphere and the hollow is
GMmd2
GMmd2⎡⎢ ⎢ ⎢⎣1−18(1−R2d)2⎤⎥ ⎥ ⎥⎦
GMmd2⎡⎢ ⎢ ⎢⎣1−18(1+R2d)2⎤⎥ ⎥ ⎥⎦
GMm8d2
The correct Answer is:B
F1=gravitational force between sphere of mass M and the particle of mass m=(GMm)/d2.
F2=gravitational force between the removed part and the particle of mass m=(GM1m)/(d−R/2)2
where M1= mass of the removed part
=43π(R2)3ρ=4πR3ρ3×8=M8
∴F2=GM1m8(d−R2)2
where M1=mass of the removed part
=43π(R2)2ρ=rπR3ρ3×8=M8 So, F2=GMm8(d−R2)2
Hence, required force
F=F1−F2=GMmd2−GMm8(d−R2)2
=GMmd2⎡⎢
⎢
⎢⎣1−18(1−R2d)2⎤⎥
⎥
⎥⎦
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-VI
Explore 42 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-II (H.W)
Explore 32 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
A spherical hollow is made in lead sphere of radius R, such that its surface touche the outside surface of the lead sphere and passes though its centre. The mass of the sphere before hollowing sphere exert on a point mass m placed at the centre of the hollow?

View SolutionFigure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was M. With what gravitational force does the hollowed out lead sphere attract a particle of mass m that lies at a distance d from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
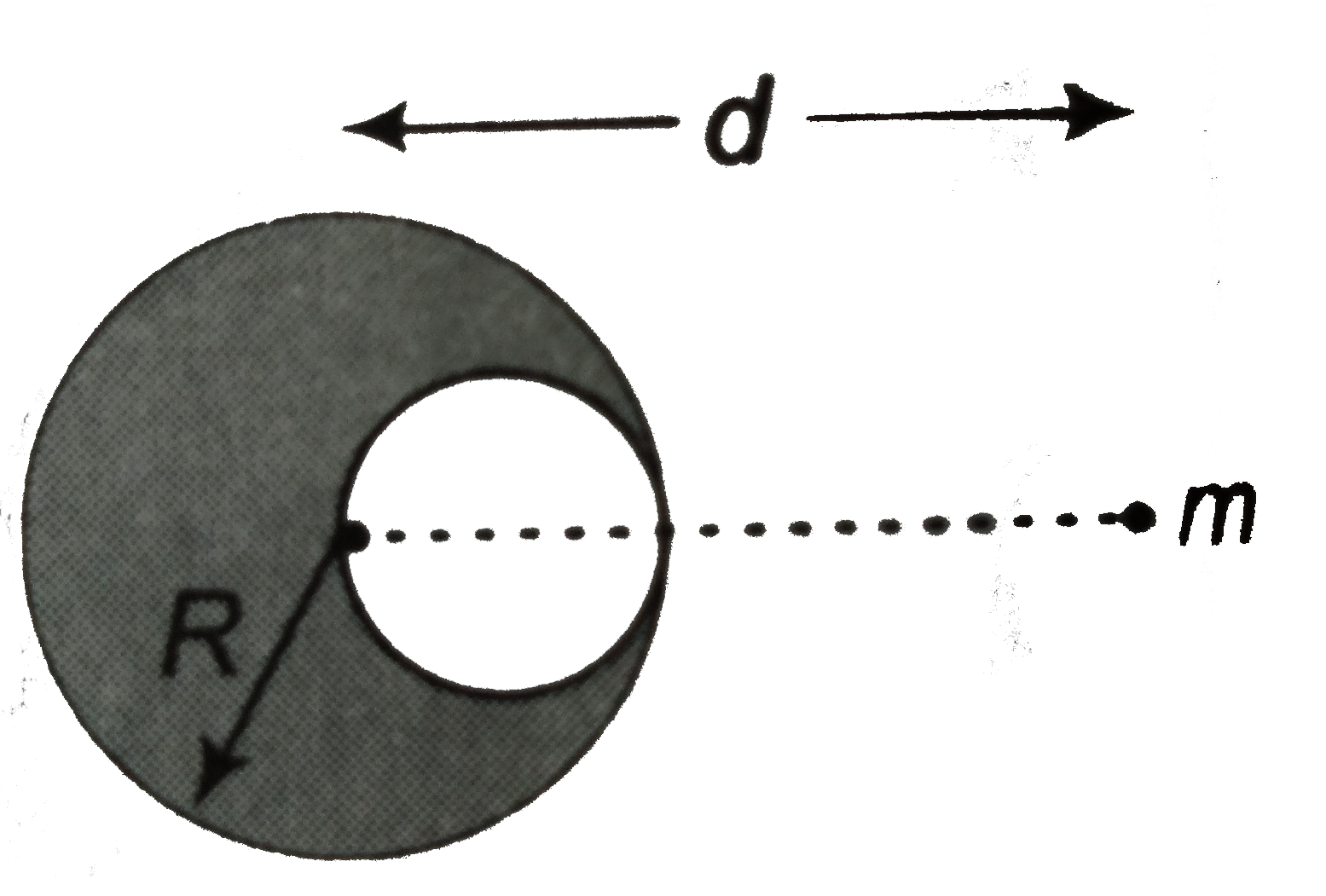
View Solution
Knowledge Check
A spherical hollow cavity is made in a lead sphere of radius R such that is surface touches the outside surface of the lead sphere and passes through its centre. The mass of the sphere before hollowing was M with what gravitational force will the hollowed out lead sphere attract a small sphere of mass m which lies at a distacne d from the centre of the lead sphere on the straight line connecting the centeres of the spheres and that of the hollow if d=2R
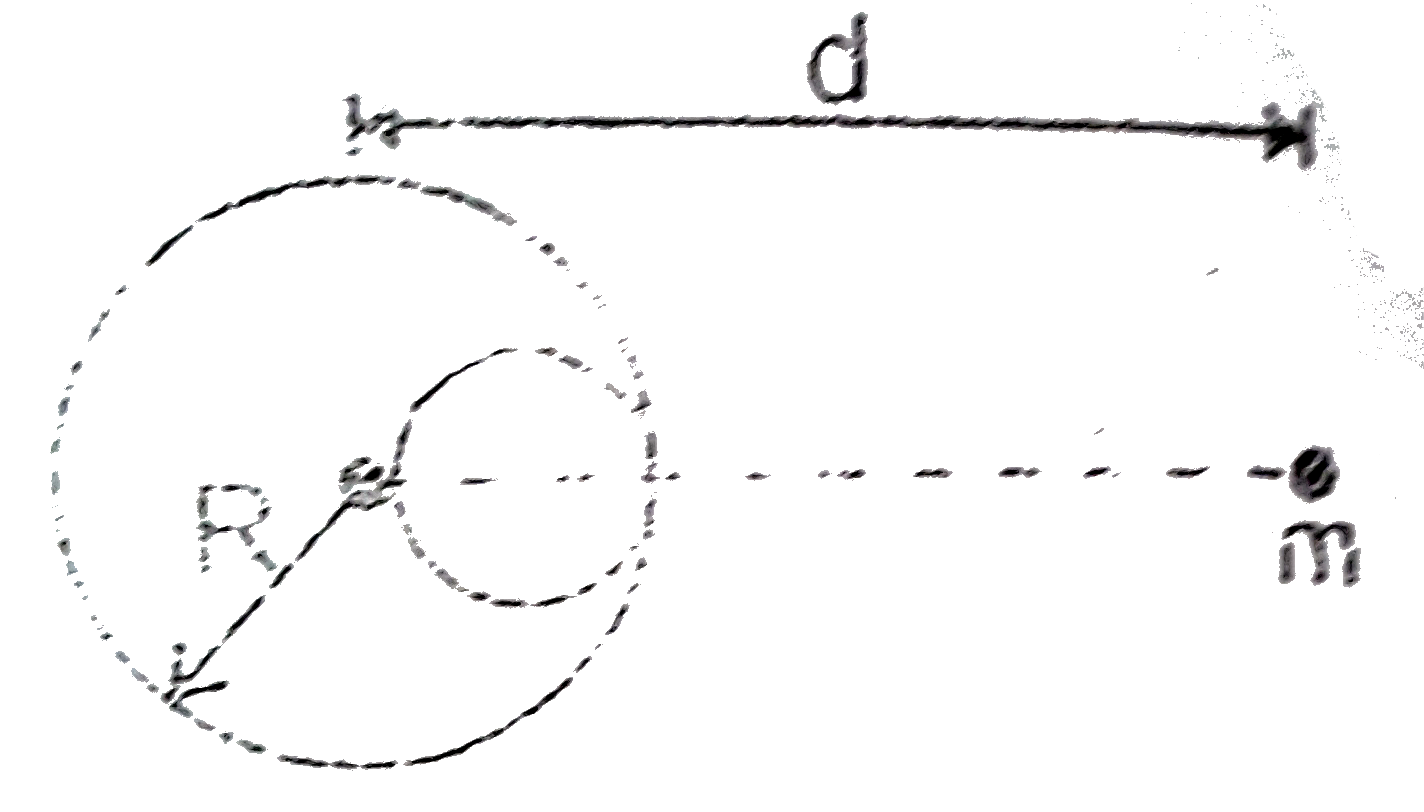 .A7GMm18R2B7GMm36R2C7GMm9R2D7GMm72R2
.A7GMm18R2B7GMm36R2C7GMm9R2D7GMm72R2A spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
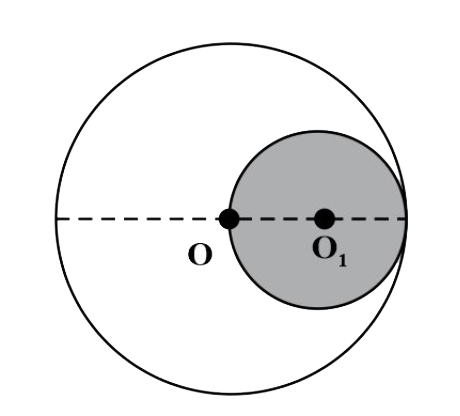 AR7BR14CR2DR
AR7BR14CR2DRA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is
 AzeroBGM8R2CGM2R2DGMR2
AzeroBGM8R2CGM2R2DGMR2
A hollow metal sphere of radius 6 cm is charged such that the potential on its surface is 12 V.What is the potential at the centre of the sphere?
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10 V. What is the potential at the centre of the sphere?
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?

View SolutionA hollow metal sphere of radius 10cm is charged such that the potential on its surface is 80 V. The potential at the centre of the sphere is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution

