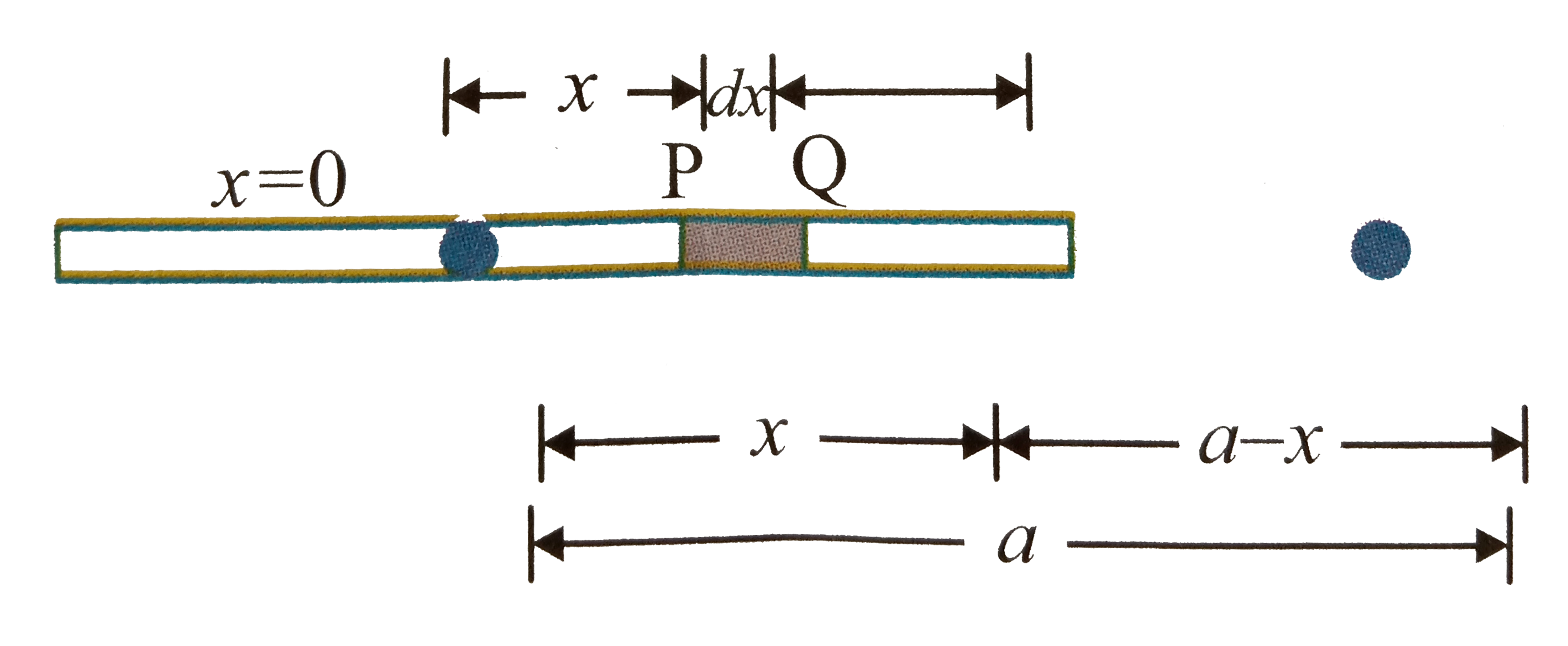
Find the potential energy of the gravitational interaction of a point mass m and a rod of mass m and length l, if they are along a straight line. Point mass is at a distance of a from the end of the rod.

Find the potential energy of the gravitational
U=−Gm2lln(2a+l2a−l)
U=−Gm2l2ln(2a+l2a−l)
U=−Gm2l2ln(2a−l2a+l)
U=−Gm2l2ln(2a−l2a+l)2
The correct Answer is:A
dm=ml.dx
dU=−Gm.(dm)(a−x)=−Gm2dxl(a−x)
U=∫1/2−1/2dU=−Gm2l∫l/2−l/2dxa−x
=−Gm2lln(a+l/2a−l/2)=−Gm2lln(2a+l2a−l)
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Find the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View Solution
Knowledge Check
Choose the most appropriate option.
The potential energy of gravitational interaction of a point mass m and a thin uniform rod of mass M and length L, if they are located along a straight line at a distance a from each other, isAU=GMmaln(a+Lα)BU=GMm(1a−1a+L)CU=−GMmaDU=−GMmLln(a+La)A point mass is placed at a distance a from one end of a rod of mass M and length l on the line which passes through the central axis of the rod. The potential energy of the system.
AU=−GMmaloge(a+1a)BU=−GMm(1a−1a+1)CU=−GMm1loge(a+1a)DU=−GMmaMoment of inertia of a uniform rod of mass m and length l is 712ml2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
Al2Bl√2Cl4Dl√3
Find the potential energy of the gravitational interaction
(a) of two mass points of masses m1 and m2 located at a distance r from each other,
(b) of a mass point of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line at a distance a from each other, also find the force of their interaction.
View SolutionFind aC and α of the smooth rod of mass m and length l.
View SolutionWhat is the gravitational potential energy of a body of mass m at a height h ?
View SolutionFind the proper potential energy of gravitational interaction of matter forming
(a) a thin uniform spherical layer of mass m and radius R,
(b) a uniform sphere of mass m and radius R(make use of the answer to Problem)
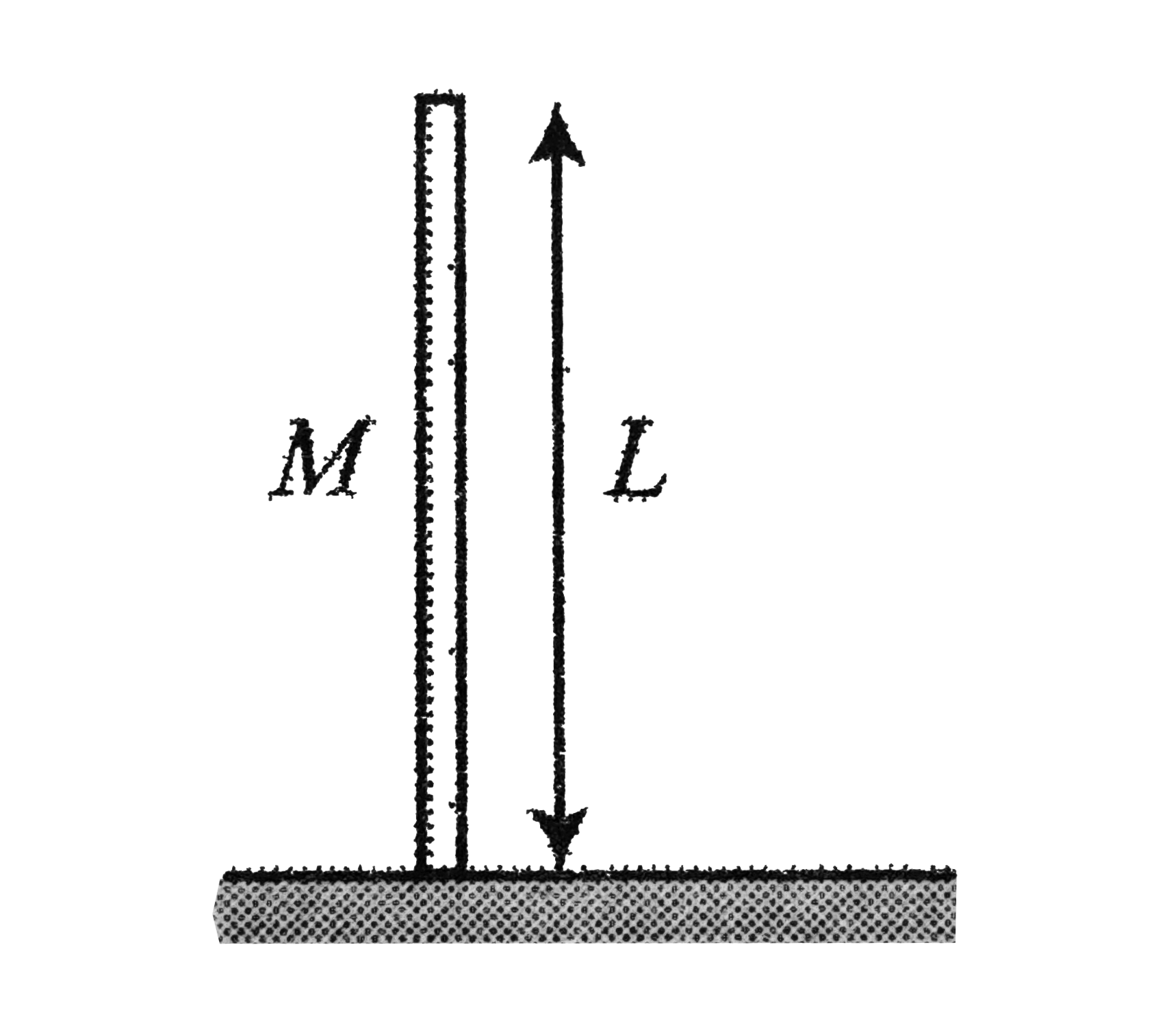
View SolutionA uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View Solution

