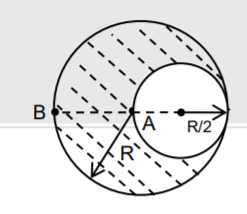
Inside a fixed sphere of radius $R$ and uniform density $ρ$ , there is spherical cavity of radius $\frac{R}{2}$ such that surface of the cavity passes through the centre of the sphere as shown in figure. A particle of mass $m_{0}$ is released from rest at centre $B$ of the cavity. Calculate velocity with which particle strikes the centre $A$ of the sphere. Neglect earth's gravity. Initially sphere and particle are at rest.

A

$\sqrt{\frac{2}{3} π G ρ R^{2}}$

B

$\sqrt{\frac{2}{3} π G ρ^{2} R^{2}}$

C

$\sqrt{\frac{2}{5} π G ρ R^{2}}$

D

$\sqrt{\frac{2}{3} π^{2} G^{2} ρ^{2} R^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Applying conservation of mechanical energy. Increases in kinetic energy =decreases in gravitational potential energy
or $\frac{1}{2} m v^{2} = U_{B} - U_{A} = m (V_{B} - V_{A})$
$v = \sqrt{2 (V_{B} - V_{A}) ... . . (i)}$
potential at $A : V_{A}$ =potential due to complete sphere -potential due to gravity
$= - \frac{1.5 G M}{R} - [- \frac{G m}{R / 2}] = \frac{2 G M}{R}$
Here, $m = \frac{4}{3} π {(\frac{R}{2})}^{3} ρ = \frac{π ρ R^{3}}{6}$ and $M = \frac{4}{3} π R^{3} ρ$
Subtituting the values, we get
$V_{B} = - \frac{G M}{R^{3}} [1.5 R^{2} - 0.5 {(\frac{R}{2})}^{2}] + \frac{1.5 G m}{R / 2}$
$= - \frac{11}{8} \frac{G M}{R} + \frac{3 G M}{R}$
$= \frac{G}{R} [\frac{π ρ R^{3}}{2} - \frac{11}{6} . π ρ R^{3}] = - \frac{4}{3} π G ρ R^{2}$
$V_{B} = V_{A} = \frac{1}{3} π G ρ R^{2}$ So, from eq.(1)
$v = \sqrt{\frac{2}{3} π G ρ R^{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid sphere having radius R and uniform charge density $ρ$ has a cavity of radius $\frac{R}{2}$ as shown in figure.Find the value of $∣ ∣ ∣ \frac{E_{A}}{E_{B}} ∣ ∣ ∣$
A $\frac{18}{19}$
B $\frac{11}{17}$
C $\frac{9}{17}$
D $\frac{9}{19}$
Question 2 - Select One or More
There is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
AElectric field intensity inside the cavity is zero if x=0
BElectric field intensity inside cavity is non-zero if $x \neq 0$
CElectric field inside the cavity is always uniform
DThe magnitude of electric field intensity inside the cavity is proportional to x.
Question 3 - Select One
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass $m$ is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass $m$ is
A $\frac{11 G M m}{R^{2}}$
B $\frac{14 G M m}{R^{2}}$
C $\frac{G M m}{2 R^{2}}$
D $\frac{G M m}{R^{2}}$

NARAYNA-GRAVITATION-LEVEL-VI

Home
Ask Doubt
Profile