A fixed sphere of radius R and uniform density ρ has a spherical cavity of radius R/2 such that the surface of the cavity passes through the centre of the sphere. A particle of mass m is located at the centre (A) of the velocity. Calculated
(a) The gravitational field at A.
(b) The velocity with which the particle strikes the centre O of the sphere. (Neglect earth's gravity)
(a) 
Mass of biger sphere=ρ43πR3=M
Mass of smaller sphere rh0.43π(R/2)3=M8
Gravitational field due to big sphere at A
EA=GM(R/2)R3=GM2R2
Gravitational field due to small sphere at A
E'A=0
(EA)net=GM2R2=Gρ.43πR32R2=23πρGR (towardsO)
(b) F=m(EA)≠t=ma
a=(2/3)πρGR
v2=u2+2as=0+2.(2/3)πρGR.R2
v=√2πGρR2/33
Topper's Solved these Questions
Similar Questions
Inside a fixed sphere of radius R and uniform density ρ, there is spherical cavity of radius R2 such that surface of the cavity passes through the centre of the sphere as shows in figure. A particle of mass m0 is released from rest at centre B of the cavity. Caculate velocity with which particle strikes the centre A of the sphere. Neglect earth's gravity. Initially sphere and particle are at rest.

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2A solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
 AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2
AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzero
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure then the value of ∣∣∣(EAEB)∣∣∣=m17 .Find the value of m
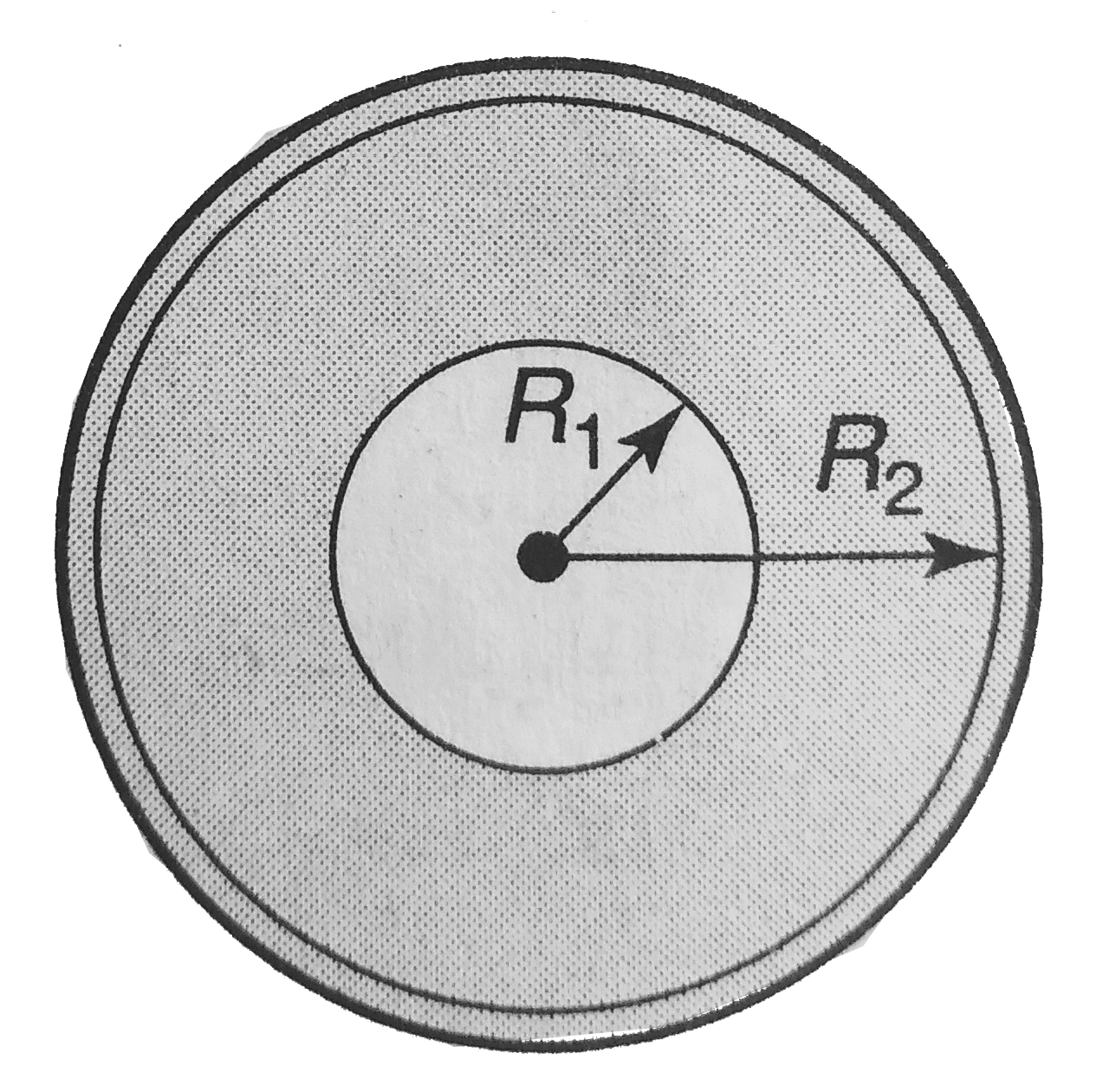
View SolutionA sphere of mass M and radiusR2 has a concentric cavity of radius R1 as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0≤r≤∞) .
View SolutionThere is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View Solution
