A solid of radius 'R' is uniformly charged with charge density in its volume. A spherical cavity of radius is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

The correct Answer is:
Step by step video, text & image solution for A solid of radius 'R' is uniformly charged with charge density rho in its volume. A spherical cavity of radius R/2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid sphere ofradius 'R' is uniformly charged with charge density ρin its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. It is given that ρR2∈0=48V. Find the electric potential at the centre C of the sphere:

View SolutionA solid conducting sphere of radius r is having a charge Q and point charges +q and -q are kept at distance d from the centre of sphere as shown in the figure. The electric potential at the centre of solid sphere
(assume potential to be 0 at infinity)
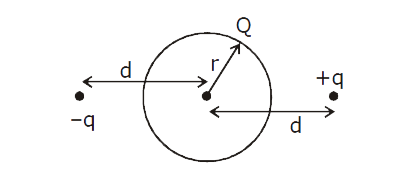
View Solution
Knowledge Check
A solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
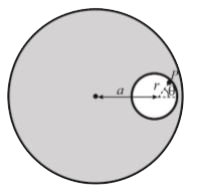 A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρaA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of theseA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
A solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?

View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density rho.It has a spherical cavity of radius R as shown in figure.The electric field at the centre of the cavity is nρR12ɛ0. Find n.
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionAn insulating solid sphere of radius R has a uniformaly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: Wgen a charge 'q' is taken from the centre to the surface of the sphere, its potential energy charges by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View Solution

