Suppose the acceleration due to gravity at earth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
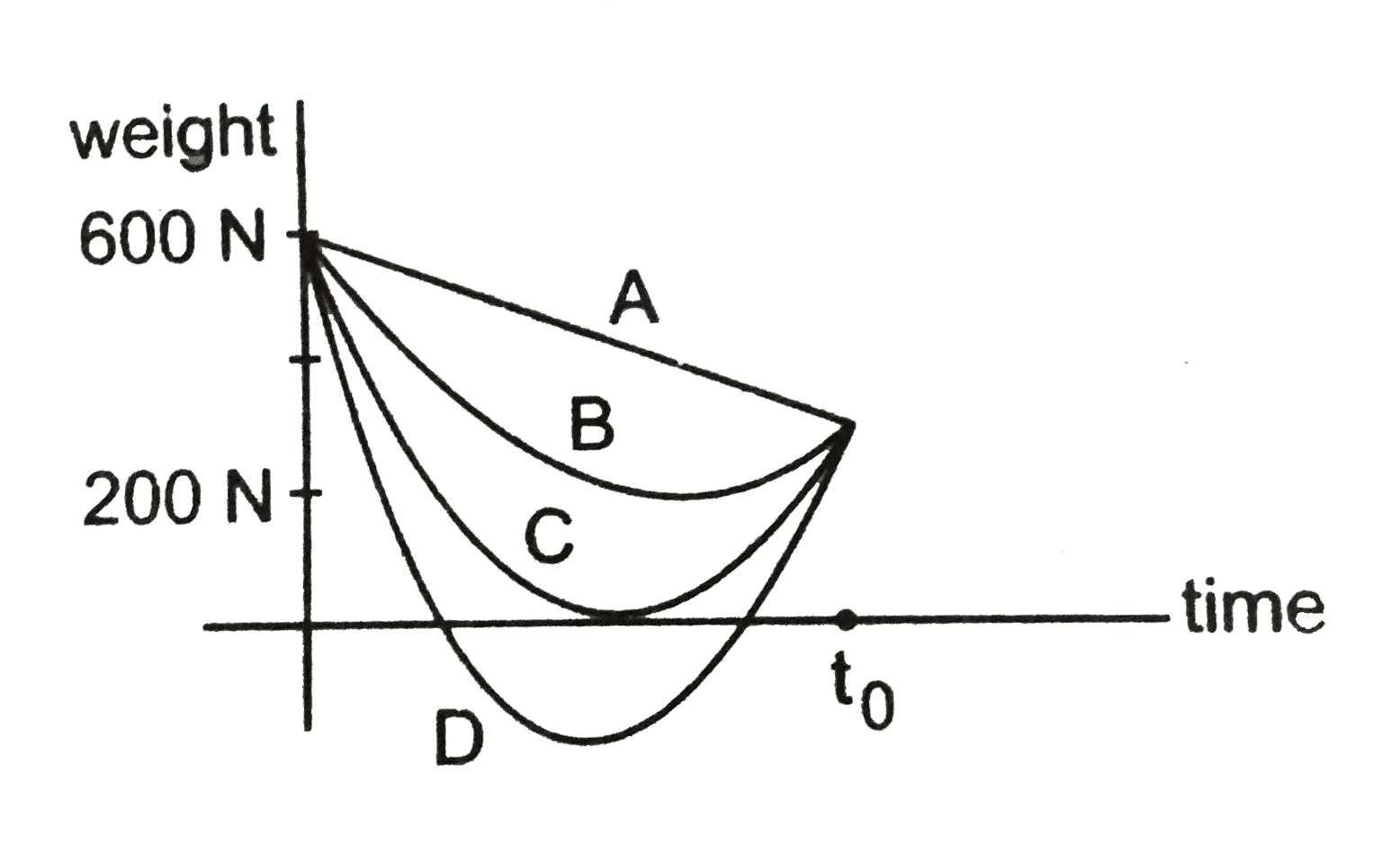
A
B
C
D
The correct Answer is:C
ge=10m/s2,gm=4m/s2
We=60,ge=600N,Wm=60,gm=240N
From going from earth to mars, at some place, gravitational pull by earth gravitational pull by mars i.e. net weight becomes zero.
Topper's Solved these Questions
Similar Questions
Suppose the acceleratio due to gravity at thth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the to the mars in a spacehip with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?

View SolutionThe acceleration due to gravity at the moon's surface is 1.67ms−2. If the radius of the moon is 1.74×106m, calculate the mass of the moon.
View Solution
Knowledge Check
Acceleration due to gravity at earth's surface is 10ms−2. The value of acceleration due to gravity at the surface of a planet of mass (15)th and radius 12 of the earth is
A4ms−2B6ms−2C8ms−2D12ms−2Let g be the acceleration due to gravity at the earth's surface and K the rotational kinetic energy of the earth. Suppose the earth's radius decreases by 2%. Keeping all other quantities constant, then
Ag increases by 2% and K increases by 2%Bg increases by 4% and K increases by 4%Cg decreases by 4% and K decreases by 2%Dg decreases by 2% and K decreases by 4%The value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
A5B10RC102RDzero
The value of acceleration due to gravity at earth's surface is 9.8ms^-1 . The altitude above its surface at which the acceleration due to gravity decreases to 4.9ms^-2 ,is close to (Take,radius of earth =6.4*10^6 m )
View SolutionThe acceleration due to gravity on the surface of the moon is 1.7ms−2. What is the time perioid of a simple pendulum on the surface of the moon, if its time period on the surface of earth is 3.5s? Take g=9.8ms−2 on the surface of the earth.
View SolutionIf accleration due to gravity on the surface of earth is 10ms−2 and let acceleration due to gravitational acceleration at surface of another planet of our solar system be 5ms−2 An astronaut weighing 50kg on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by
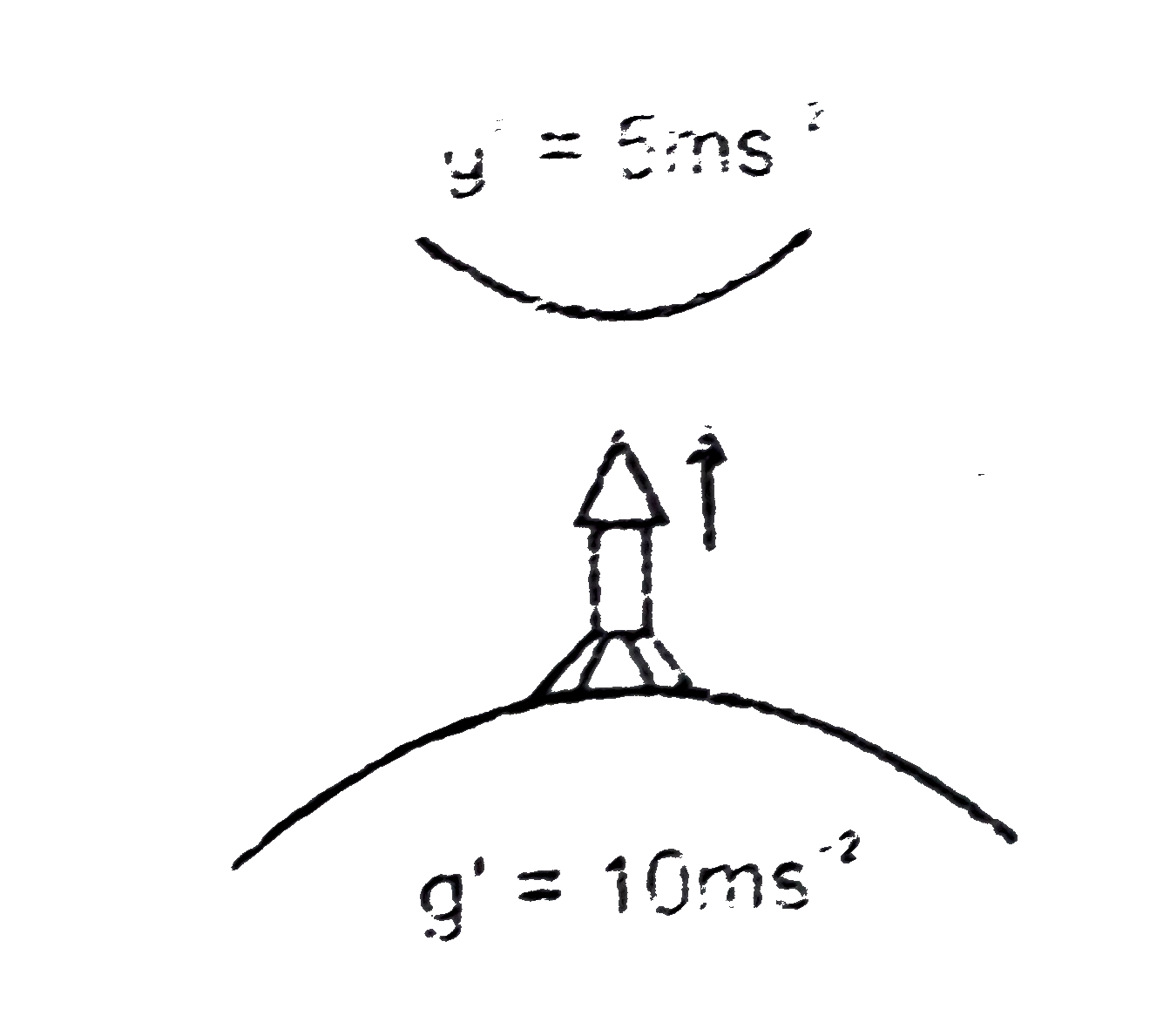 .
.
View SolutionThe value of acceleration due to gravity at earth's surface is 9.8ms−2. The altitude above its surface at which the acceleration due to gravity decreases to , is close to: (radius of earth =6.4×106m)
View SolutionThe acceleration due to gravity at the poles is 10ms−2 and equitorial radius is 6400km for the earth. Then the angular velocity of rotaiton of the earth about its axis so that the weight of a body at the equator reduces to 75% is
View Solution

