A particle of mass m is placed on centre of curvature of a fixed, uniform semi-circular ring of radius R and mass M as shown in figure. Calculate:
(a) interaction force between the ring and the particle and
(b) work required to displace the particle from centre of curvature to infinity.

(a)F=2GMπR2,(b)GMR
(a)F=2GMmπ2R,(b)GMmR2
(a)F=−2GMmπR2(b)−GMmR
(a)F=2GMmπR2(b)GMmR
The correct Answer is:D
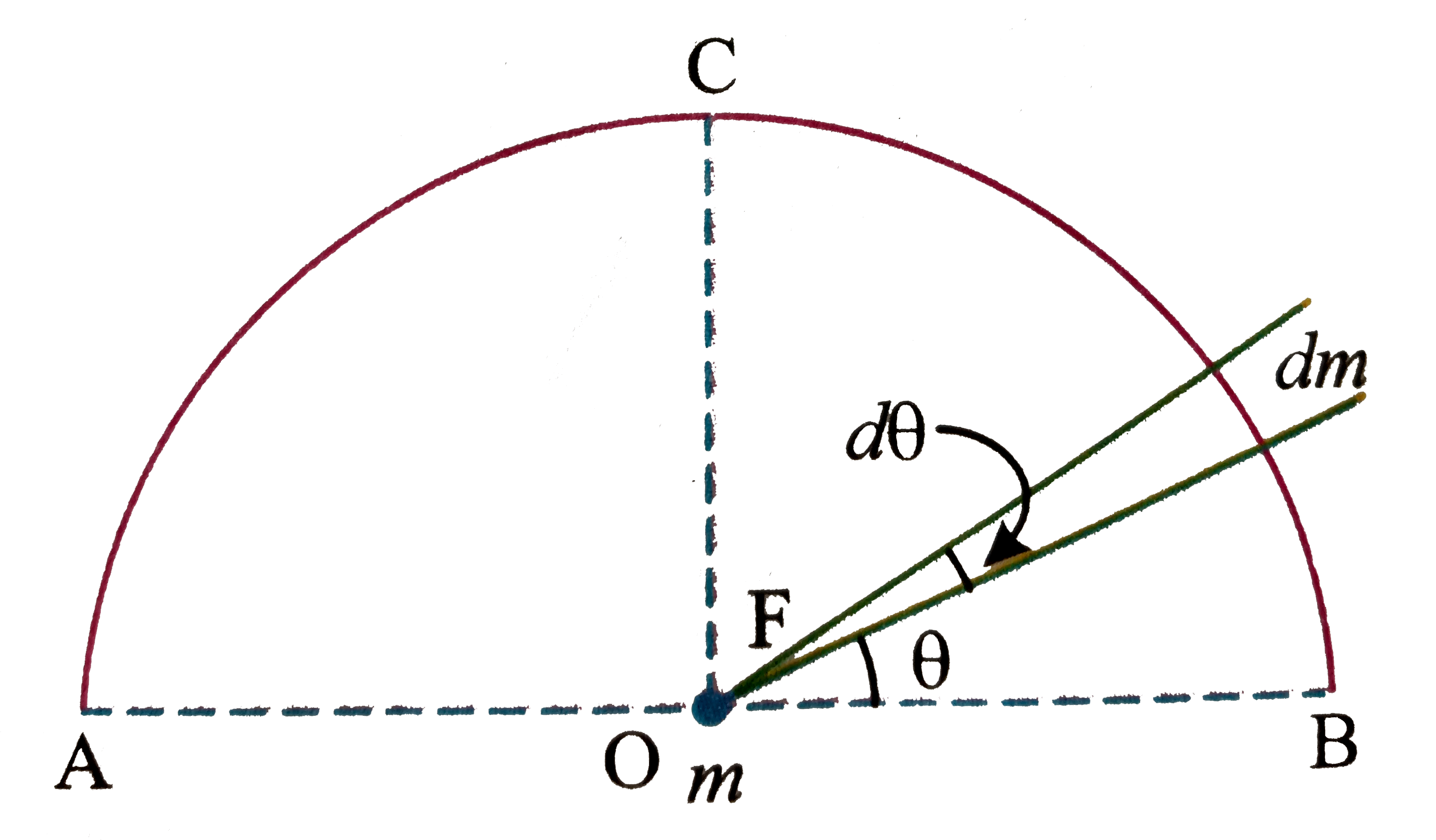
dM=(MπR)(Rdθ)=Mπ.dθ
Required force =∫π/202Fsinθ (towards C)
=∫π/202Gm(dM)R2sinθ
=∫π02GMmπR2sinθ.dθ=2GMmπR2
(b)U=−GMmR
∴ Binding energy =|U|=GMmR
i.e., this much energy is required to displace the particle from centre of curvature to infinity.
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Knowledge Check
The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
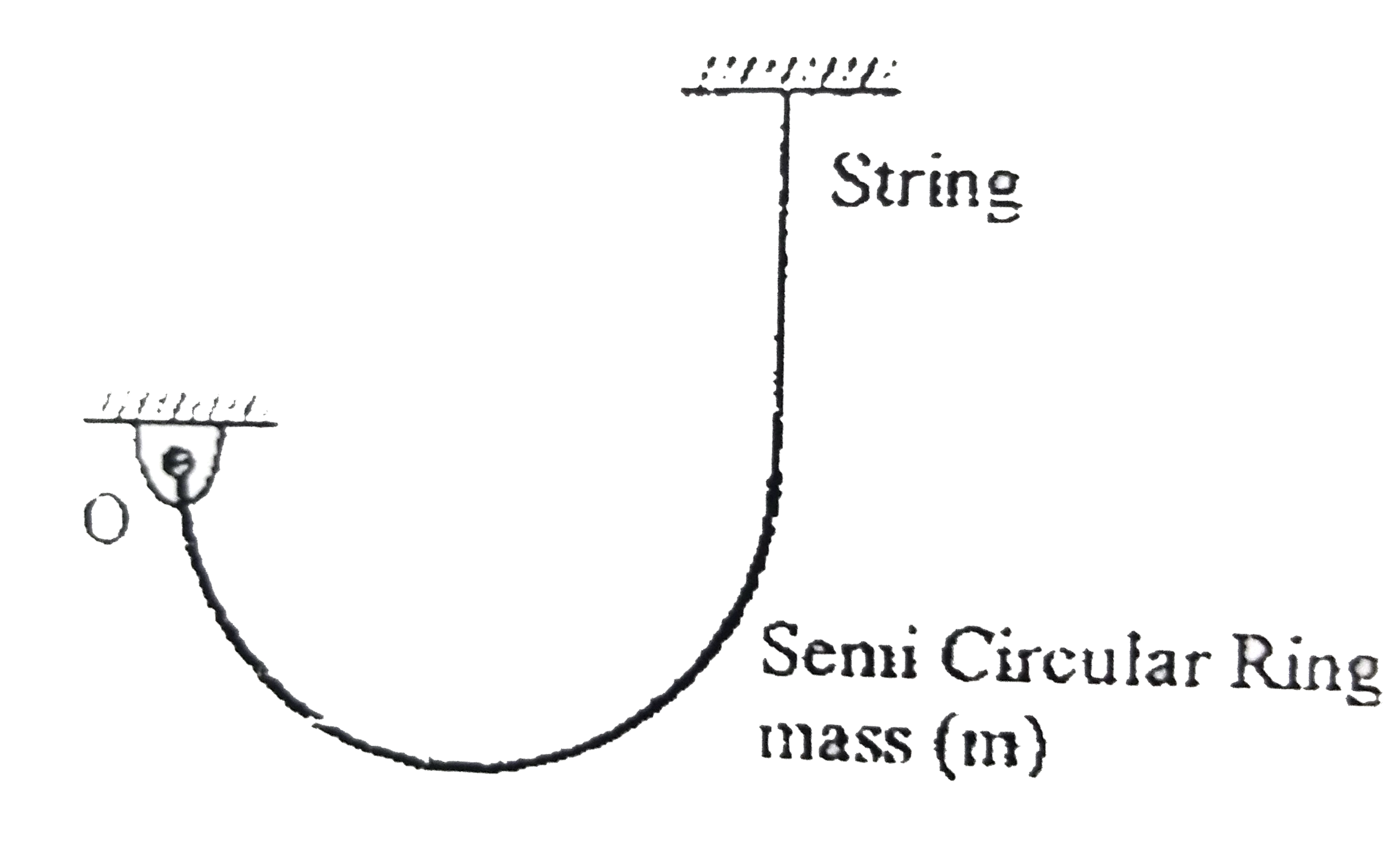 ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.The centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance √8R apart as shown. The force of attraction between the ring and the sphere is
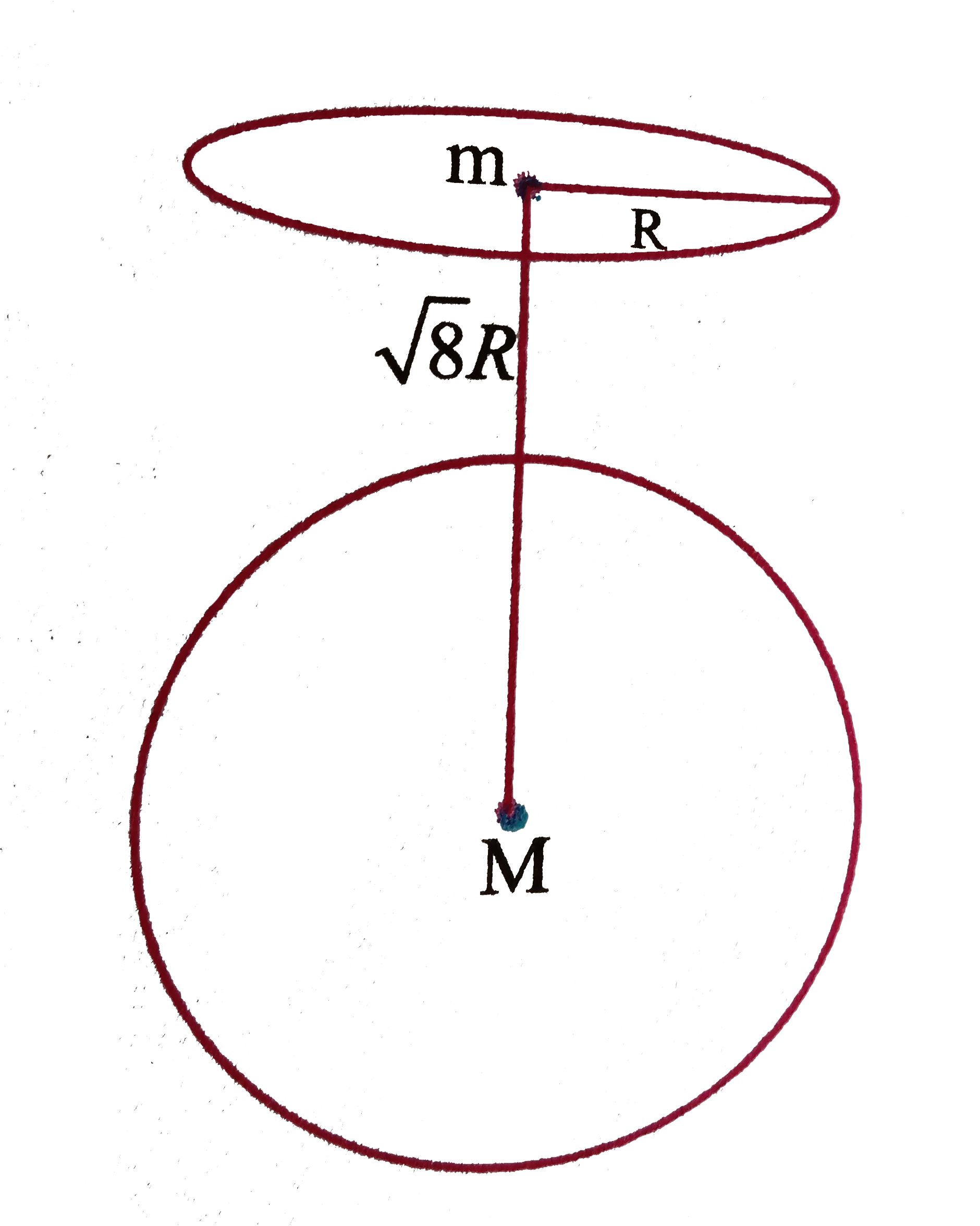 A2√227GmMR2BGmM8R2CGmM9R2D√29GmM9R2
A2√227GmMR2BGmM8R2CGmM9R2D√29GmM9R2
A small point mass m is placed at the centre of curvature of acircular are of radius R and mass 3 m as shown in figure−6.31.Find the net gravitational force acting on the point mass.

View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View Solution" The force of attraction on a particle of mass "m" placed at the centre of curvature of a semicircular wire of length L and mass "M" is "
View SolutionMoment of inertia of a uniform circular ring of mass M and radius R about a diameter of ring is………………. .
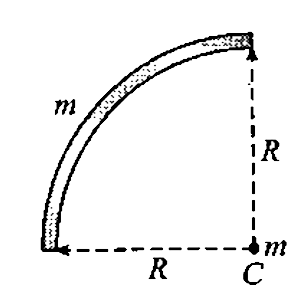
View SolutionFind the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
View SolutionA particle of mass m was transferred from the centre of the base of a uniform hemisphere of mass M and radius R into infinity.
What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?
View Solution

