Given a thin homogenous disc of radius a and mass m1. A particle of mass m2 is placed at a distance l from the disc on it's axis of symmetry. Initially both are motionless in free space but they ultimately collide because of gravitational attraction. find the relative velocity at the time of collision. assume a<<1.
[2G(m1+m2)(2a−1l)]
[2G(m1+m2)(2a−1l)]12
[2G(m1+m2)(2a−1l)2]
[2G(m1+m2)2(1a−1l)]
The correct Answer is:B
Potential at centre of disc is
V=∫a0−G(dm)r=∫a0−G(m1πa2)(2πr.dr)r
=−2Gm1a
Now applying conservation of mechanical energy, decreases in gravitational P.E.=increases in K.E. or 12μv2r=Ui−Uf, here μ=reduced mass =m1m2m1+m2 and vr=relative speed.
∴12(m1m2m1+m2)v2r=[−Gm1m2l−(−2Gm1m2a)]
∴vr=√2G(m1+m2)(2a−1l)
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
The mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View Solution
Knowledge Check
Two particles of mass m and M are initialljy at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when d is their separation at any instant
A√2G(M+m)dB√G(M+m)dC√G(M+m)2dD√G(M+m)4dTwo point masses m1 and m2 at rest in gravity free space are released from distance d. Find the velocity of the CM of the system at the time of collision of particles
AZeroB2C3DNoneFind moment of inertia of half disc of radius R2 and mass M about its centre. A smaller half disc of radius R1 is cut from this disc
 AM4(R21+R22)BM8(R21+R22)CM16(R21+R22)DM32(R21+R22)
AM4(R21+R22)BM8(R21+R22)CM16(R21+R22)DM32(R21+R22)
Two particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when their separation is d.
View SolutionFind the gravitational interaction energy of system consisting of a disc of mass M, radius R and a small mass m dituated at a distance x from disc centre on its axis as shown in figure.

View SolutionTwo particles of mass 'm' and 3 m are initially at rest an infinite distance apart. Both the particles start moving due to gravitational attraction. At any instant their relative velocity of approach is íGmd where 'd' is their separation at that instant. Find ne.
View SolutionA particle of mass m strikes elastically with a disc of radius R, with a velocity →v as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, find the velocity of the disc just after the collision.

View Solution(a) A uniform rod of mass M and length L is placed at distance L from a point mass m as shown. Find force on m
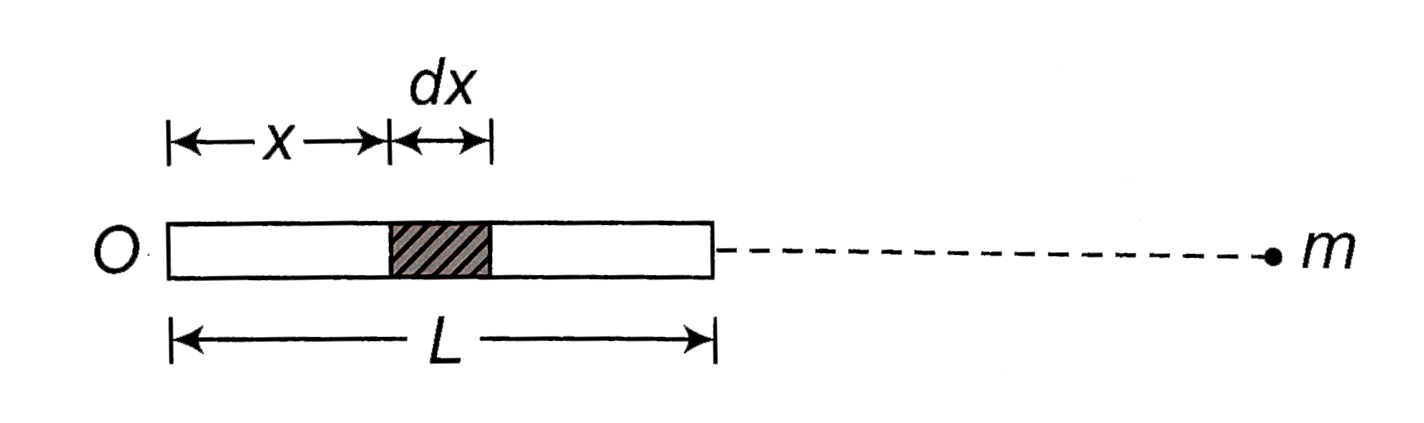
(b) A semiconductor wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. find the gravitational attraction on the particle due to the wire.
View Solution

