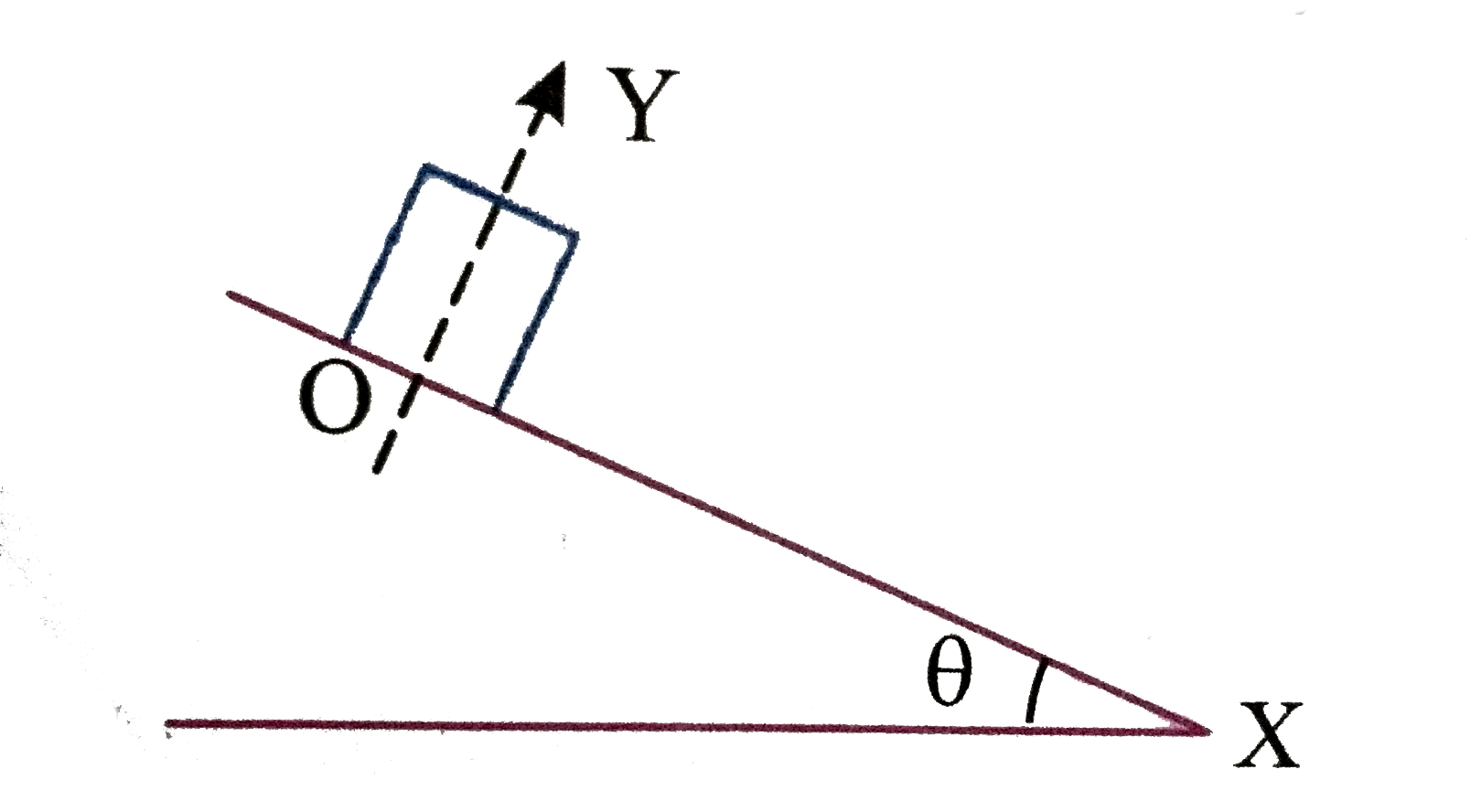
In the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O.
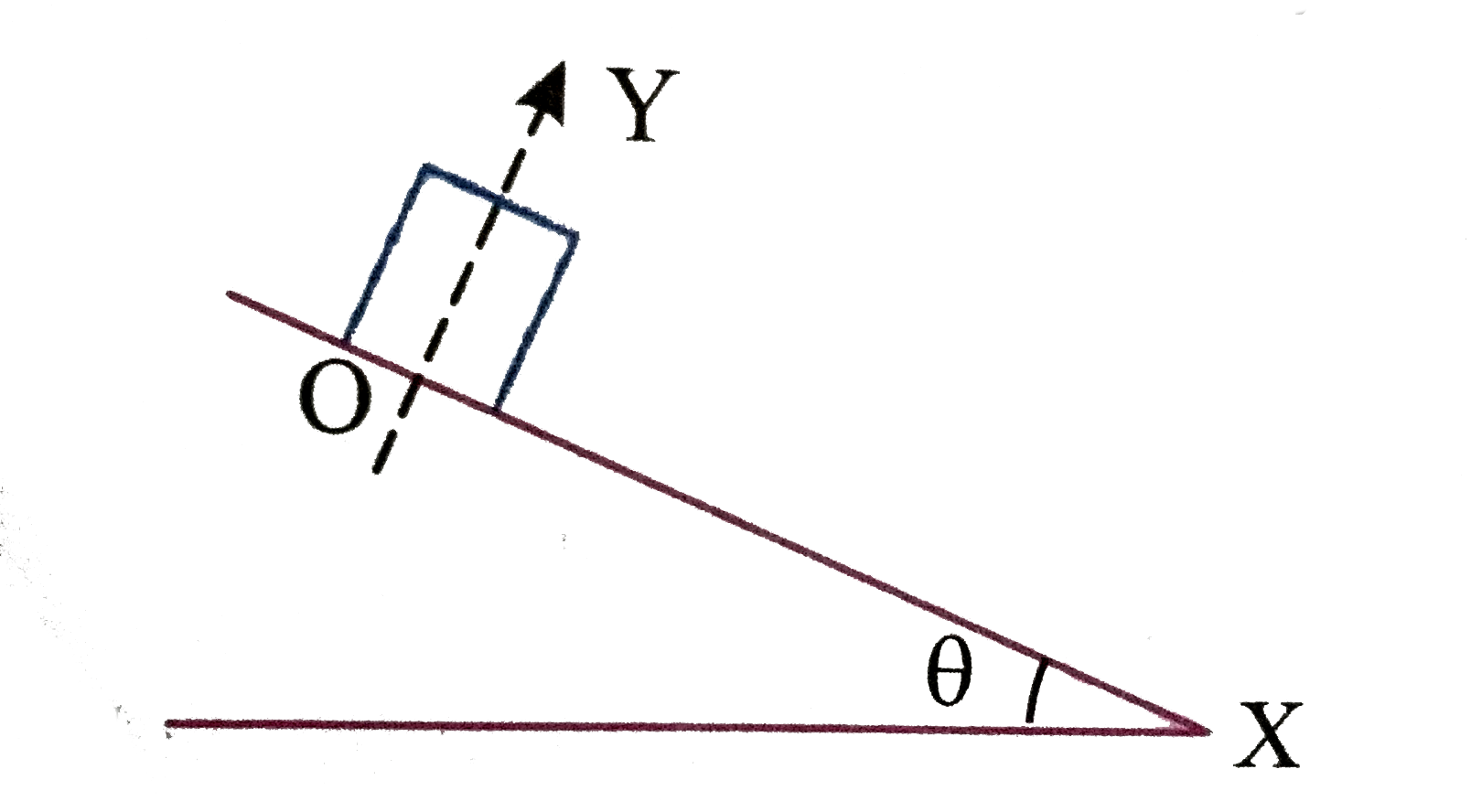
The maximum velocity of block will be:
√g
√gsinθ
√gcosθ
√gtanθ
The correct Answer is:B
At any position =g(sinθ−kxcosθ)
a=gsinθ(1−x)vdvdx=gsinθ(1−x)
⇒v∫0vdv=x∫0gsin(1−x)dxv22=gsinθ(x−x22)
v will max when a=0⇒x=1vmax=√gsinθ
Topper's Solved these Questions
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
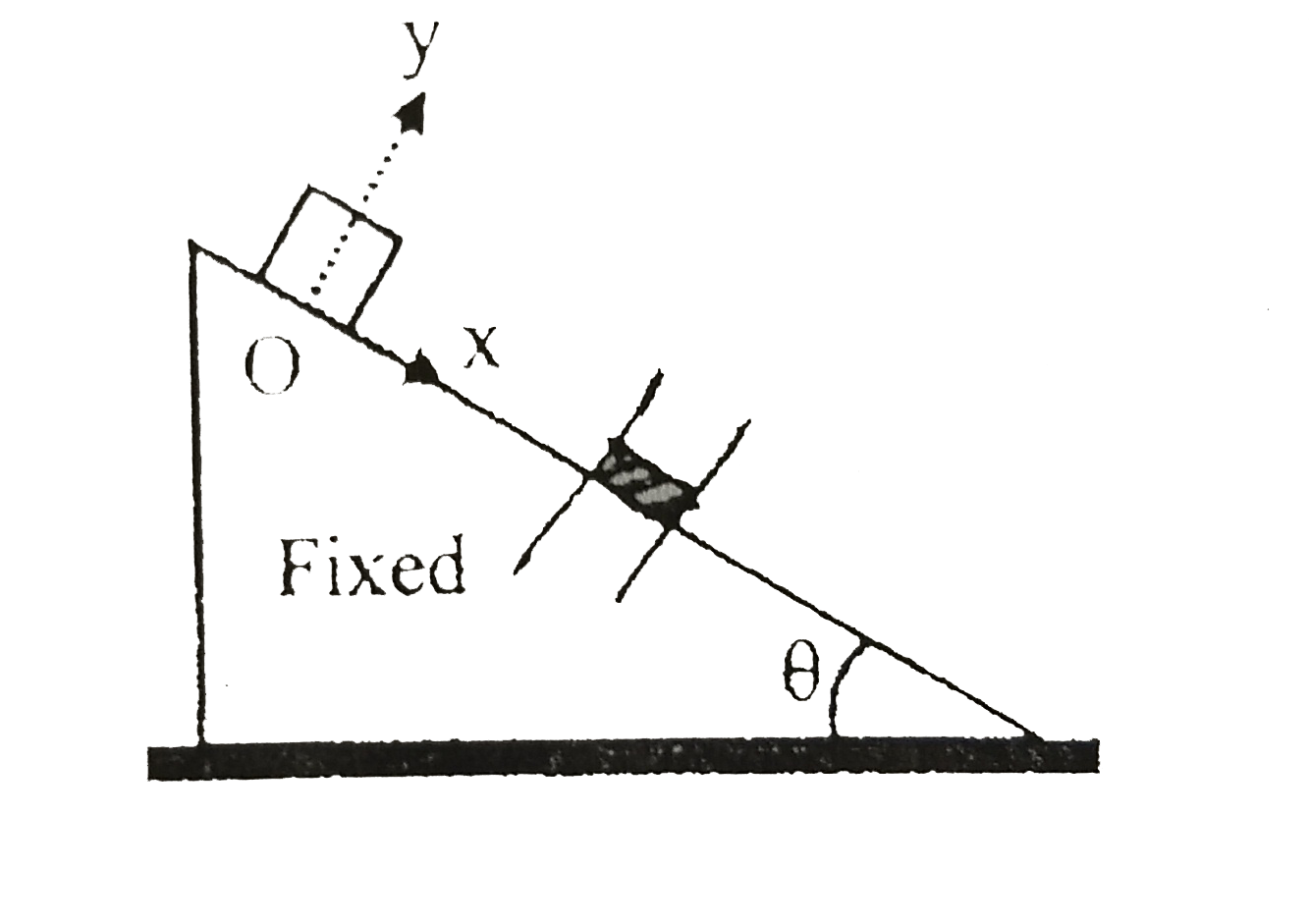
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
Frictional force acting on the block after it comes to rest :
View Solution
Knowledge Check
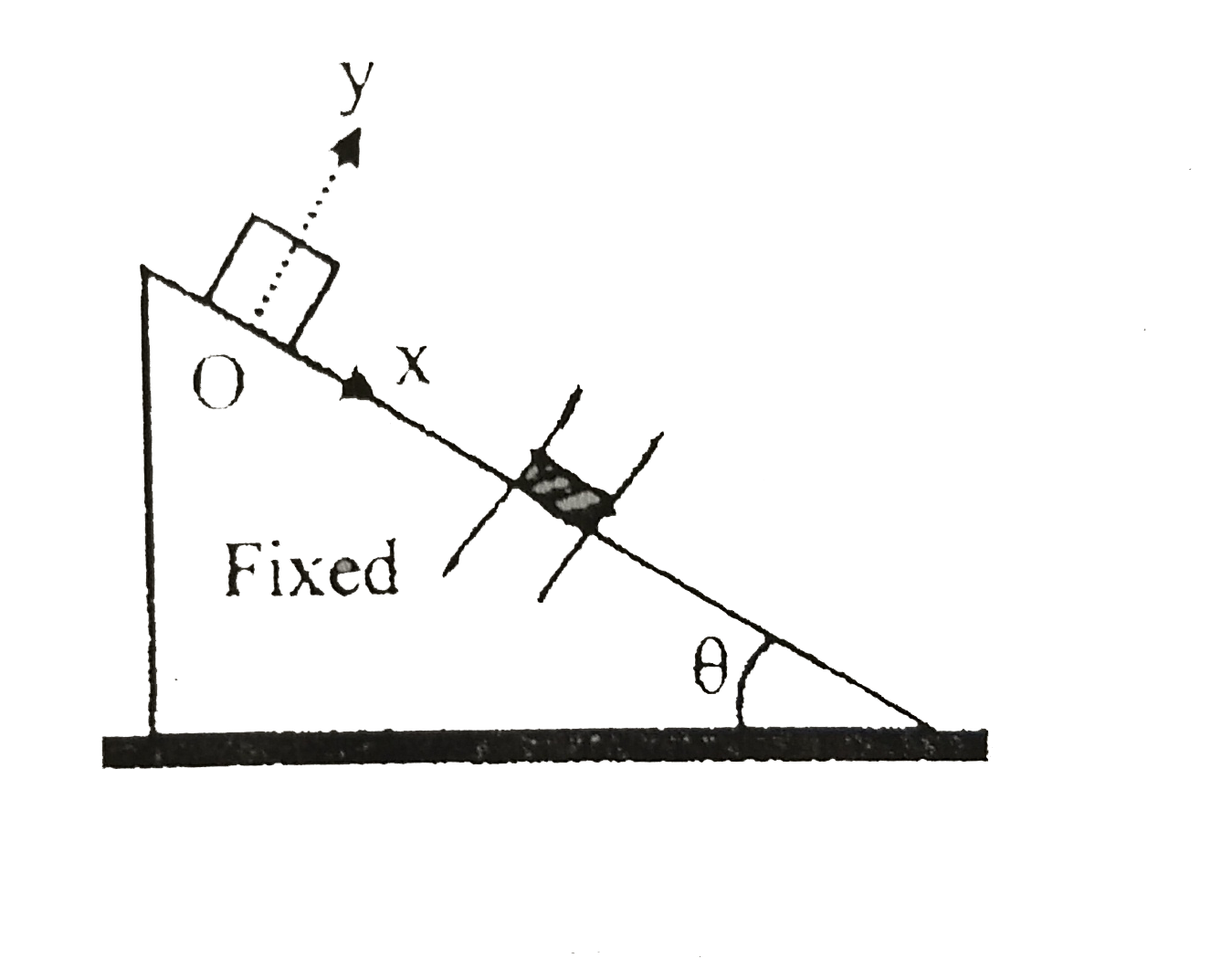
In the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
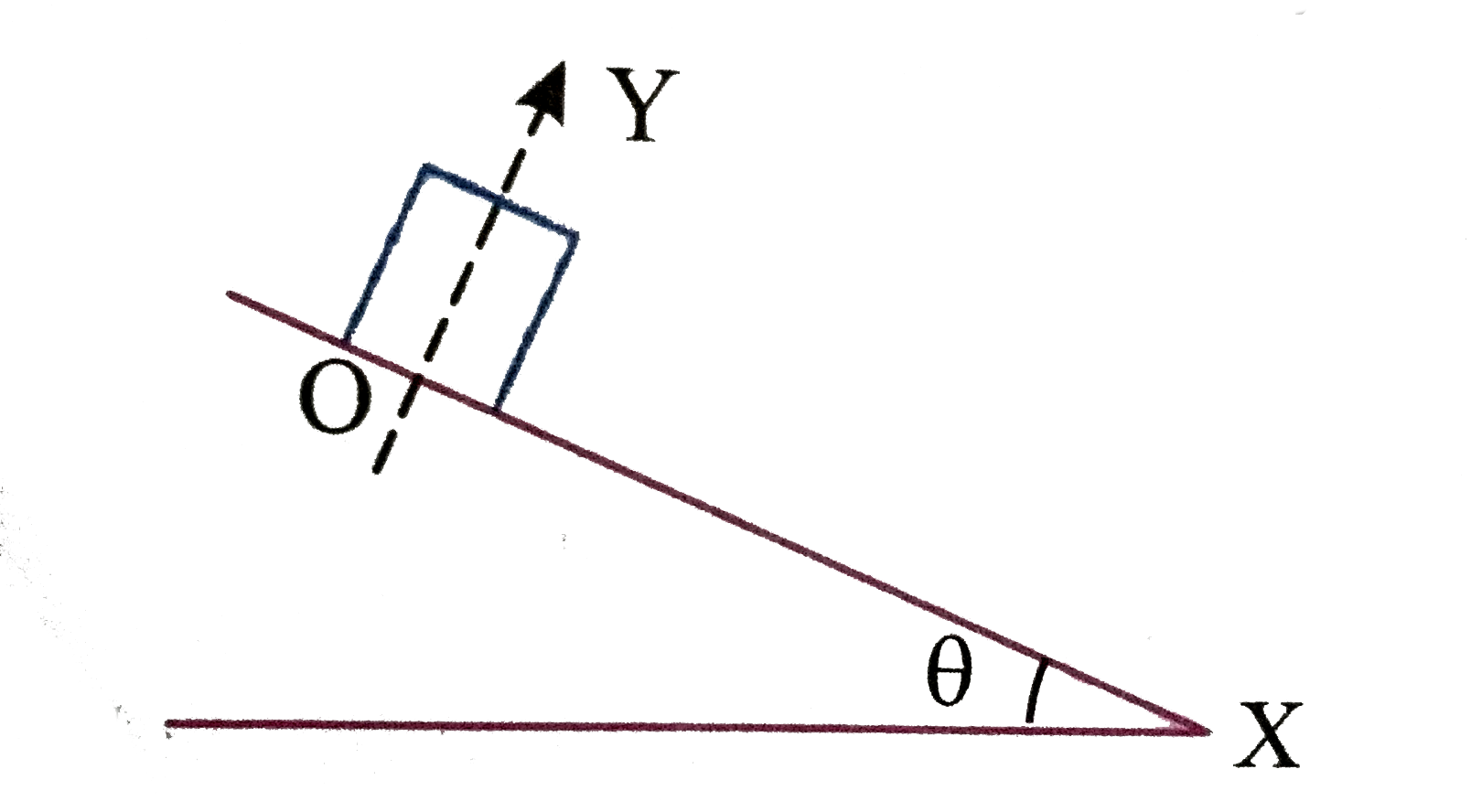
Maximum distance traveled by block:A1mB2mC3mD12mIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
Maximum distance traveled by the block :A1 mB2 mC3 mD12 mIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
Frictional force acting on the block after it comes to rest:AmgsinθB2mgsinθCmgsinθ2D2mgcosθ
In the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
Frictional acting on the block just before it comes to rest :
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane and y-axis perpendicular to the inclined plane. Te coefficient friction varies with x as μ=kx, where k=tanθ. A block is released at O.
The maximum velocity of block will be
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane and y-axis perpendicular to the inclined plane. Te coefficient friction varies with x as μ=kx, where k=tanθ. A block is released at O.
Frictional force acting on the block just before it comes to rest
View SolutionA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .
.
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
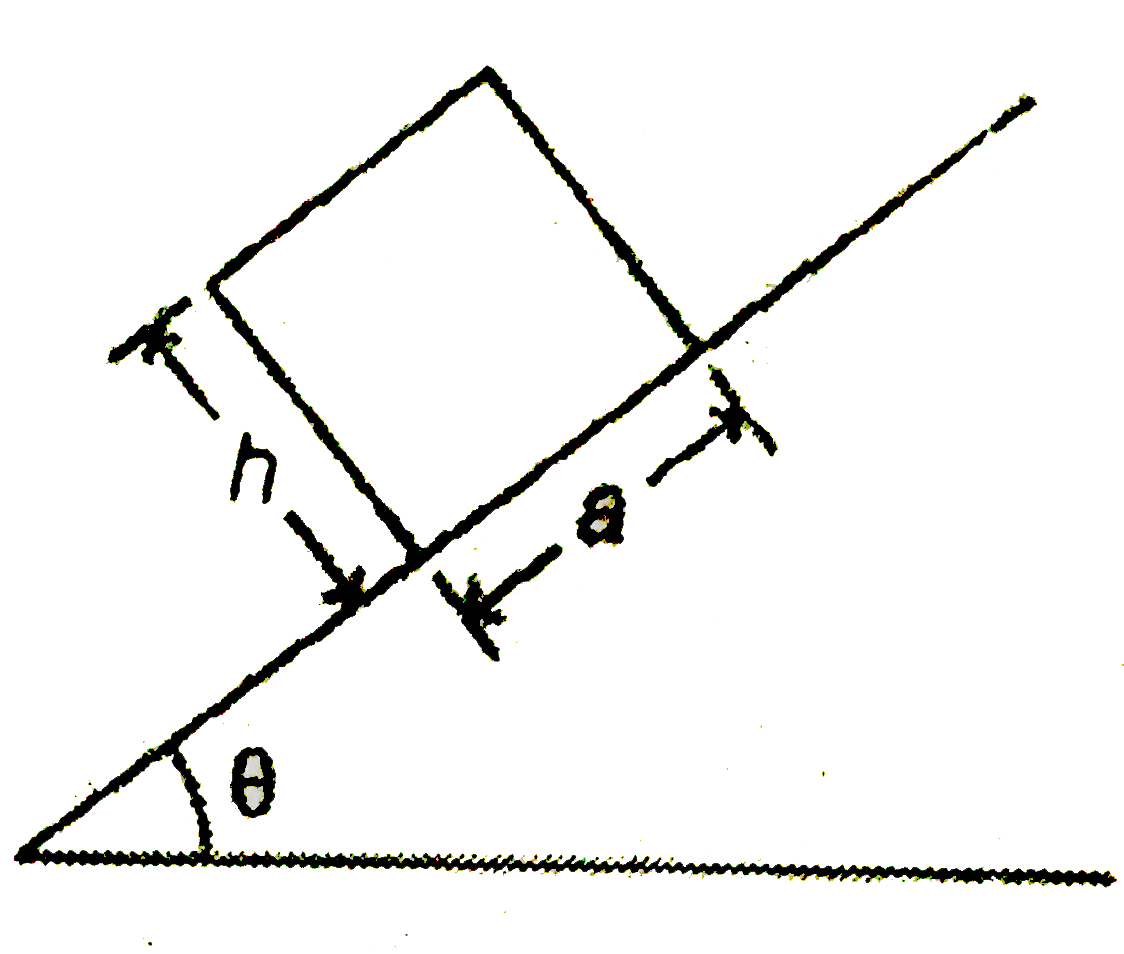
View Solution

