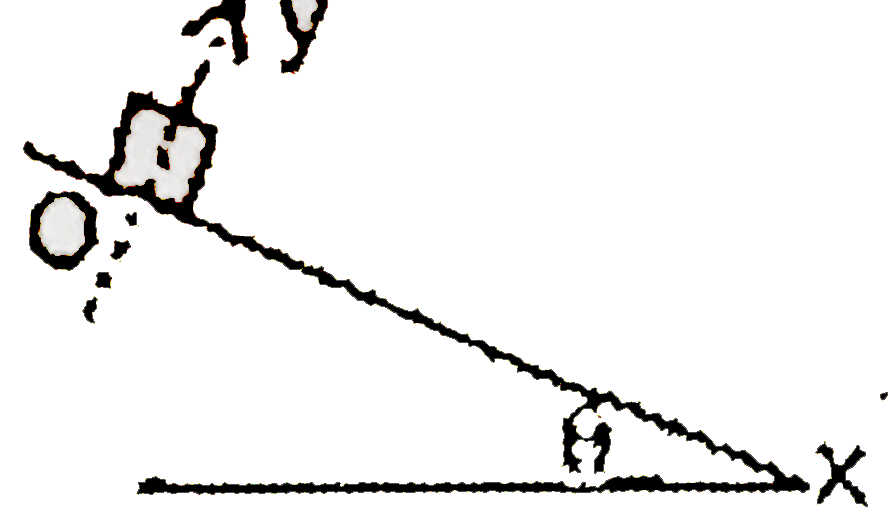
In the adjacent figure, x-axis has been taken down the inclined plane and y-axis perpendicular to the inclined plane. Te coefficient friction varies with x as μ=kx, where k=tanθ. A block is released at O.
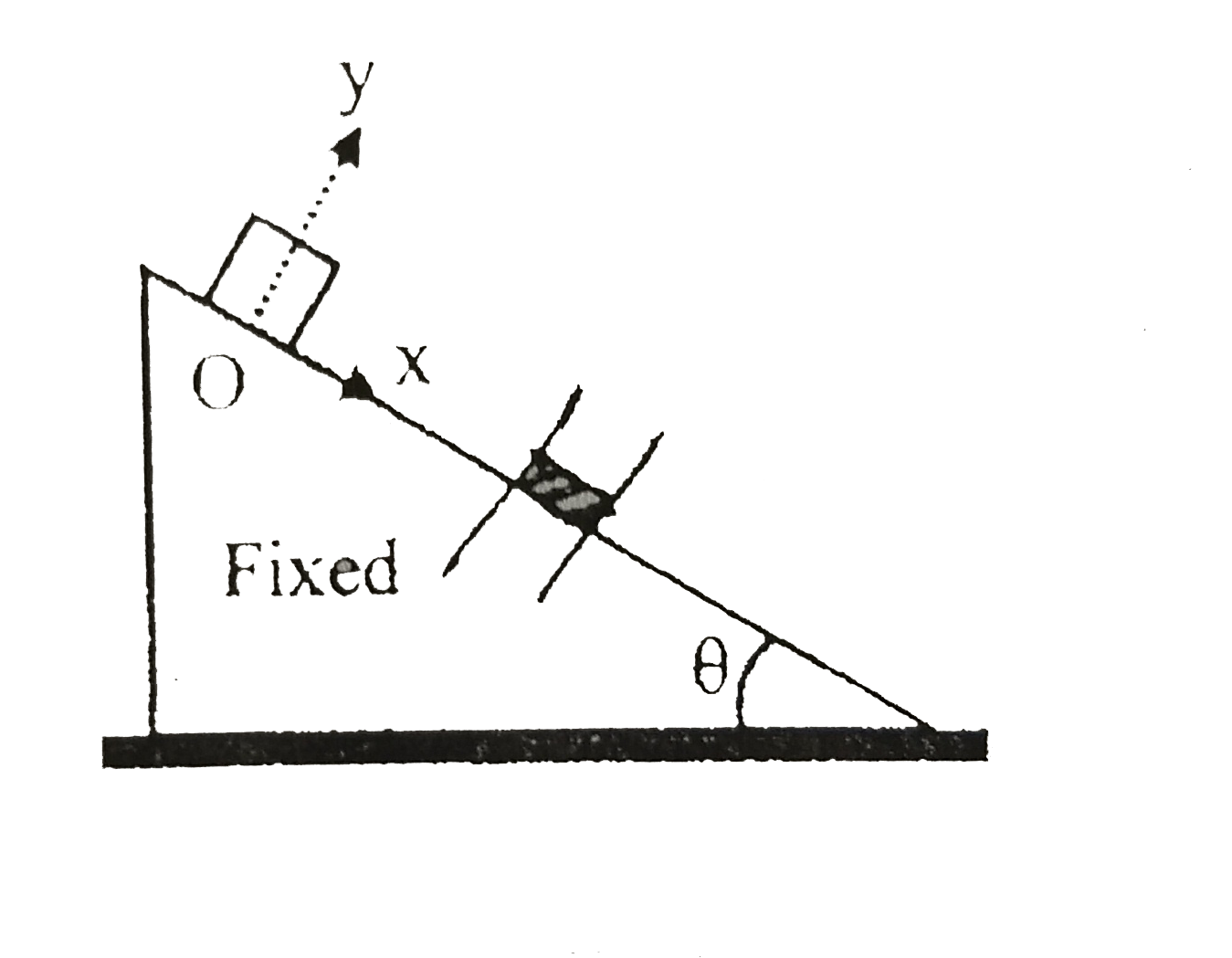
The maximum velocity of block will be
√g
√gsinθ
√gcosθ
√gtanθ
The correct Answer is:B
From figure
mgsinθ−μmgcosθ=ma
a=g(sinθ−kxcosθ)
=g(sinθ−sinθ.X)
∴a=gsinθ(1−x)

for vmax,vdvdx=gsinθ(1−x)......(i)
Speed will be maximum when acceleration = 0
gsinθ(1−x)=0⇒x=1
From equation (i)
⇒∫v×dv=∫gsinθ(1−x)dx
⇒v22=gsinθ×x−gsinθ×x22.....(ii)
∴v2max2=gsin2⇒vmax=√gsinθ
Fx=kx×mgcosθ=tanθx×mgsinθ=x×mgsinθ...(iii)
From equation (ii)
v22=gsinθ×x−gsinθ×x22
when block will be at rest then v=0
0=gsinθ×x−gsinθ×x22⇒x=2
Putting value of x in equation (iii) we get
Fx=2mgsinθ
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART B
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICA PART A
Explore 12 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (C )
Explore 15 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
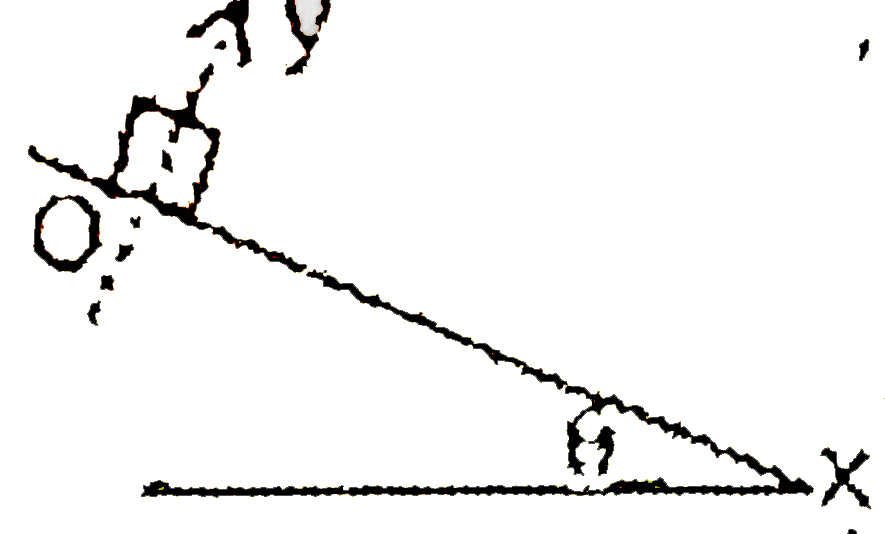
Maximum distance traveled by the block :
View Solution
Knowledge Check
In the adjacent figure, x-axis has been taken down the inclined plane and y-axis perpendicular to the inclined plane. Te coefficient friction varies with x as μ=kx, where k=tanθ. A block is released at O.
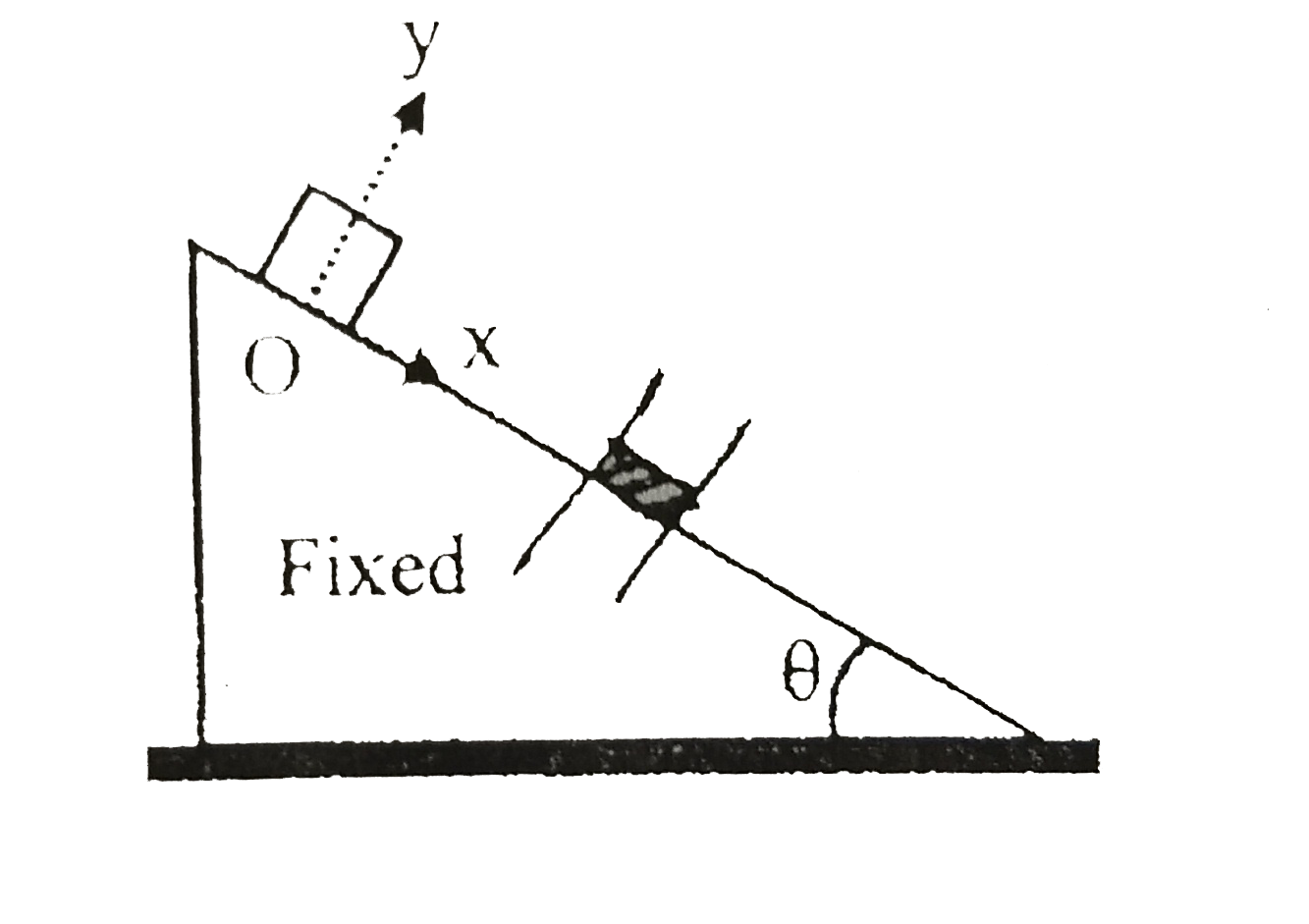
Frictional force acting on the block just before it comes to restAmgsinθB2mgsinθCmgsinθ2D2mgcosθIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O.
The maximum velocity of block will be:A√gB√gsinθC√gcosθD√gtanθIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
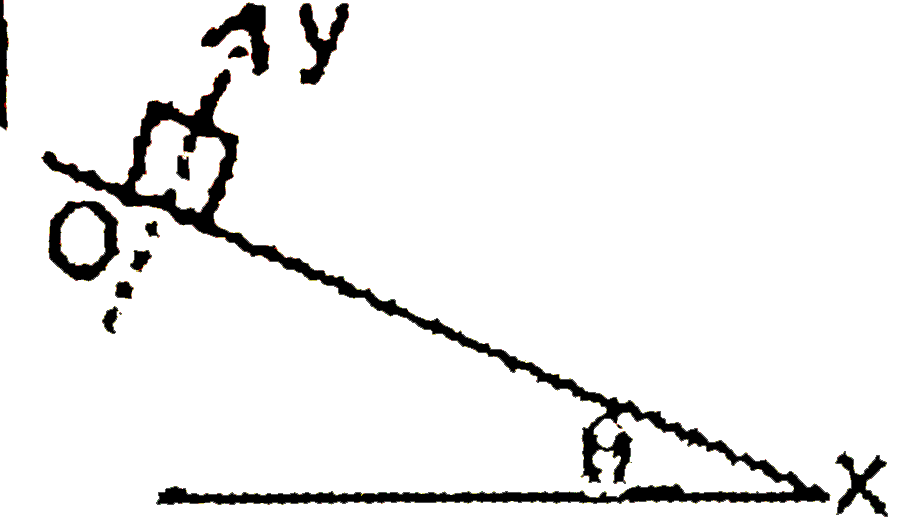
The maximum velocity of block will be :A√gB√gsinθC√gcosθD√gtanθ
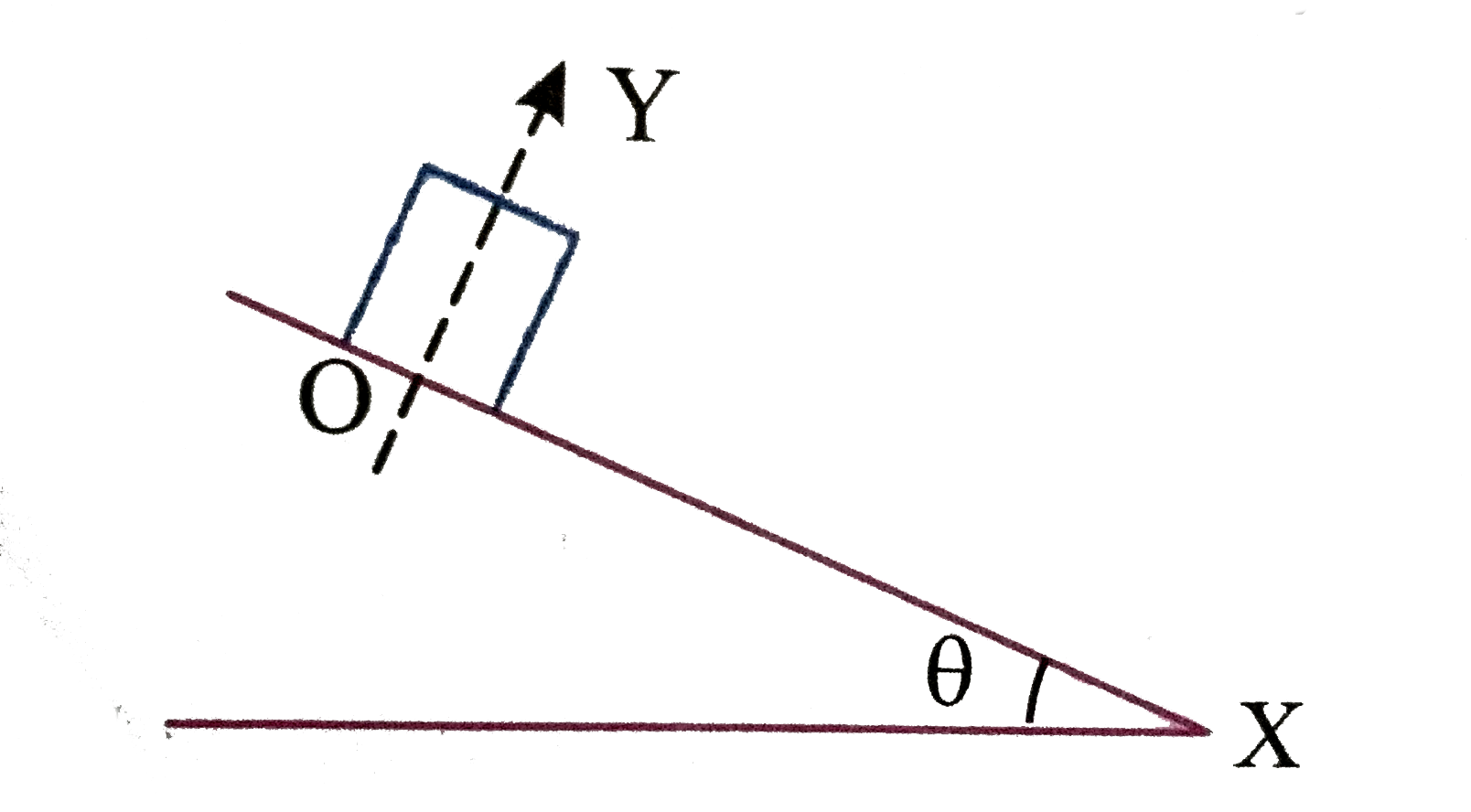
In the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
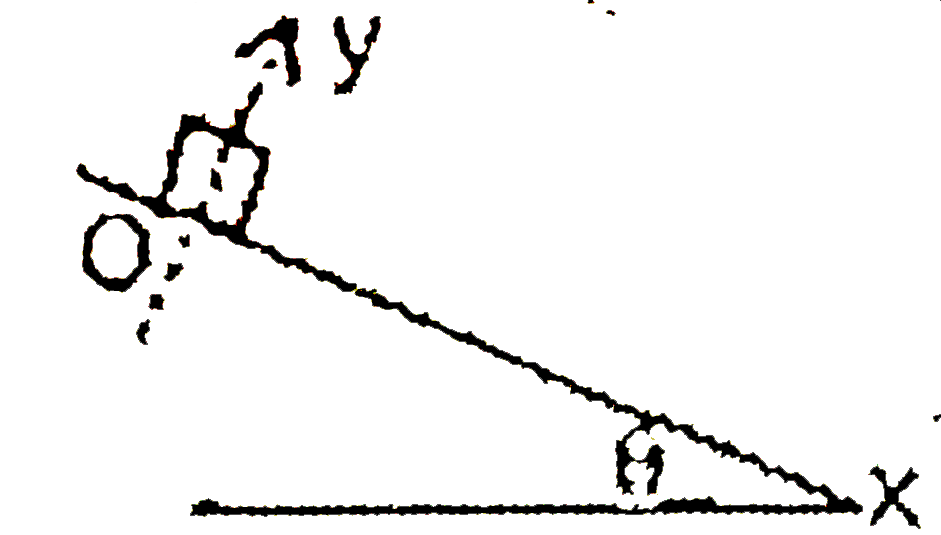
Frictional force acting on the block after it comes to rest :
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
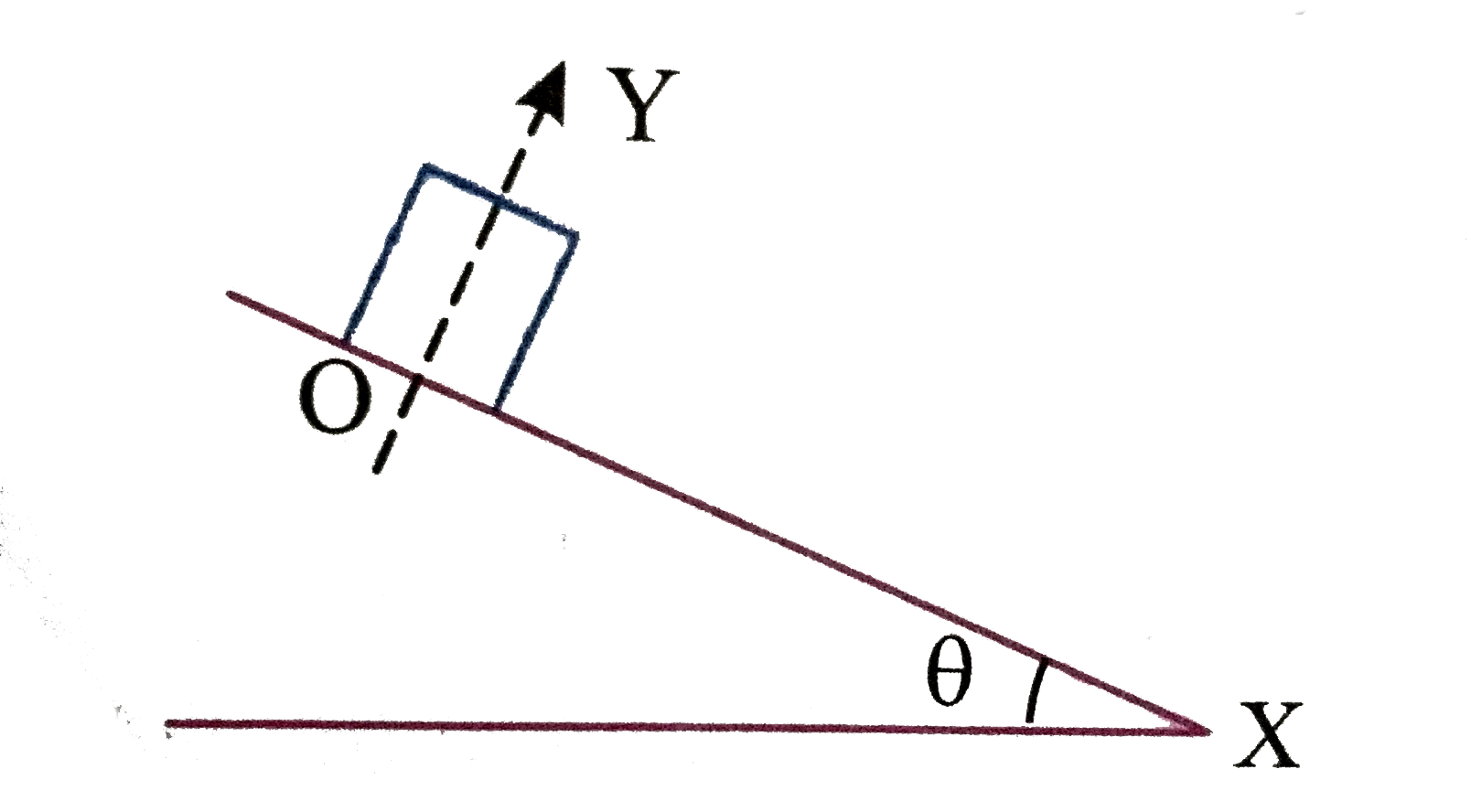
Maximum distance traveled by block:
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
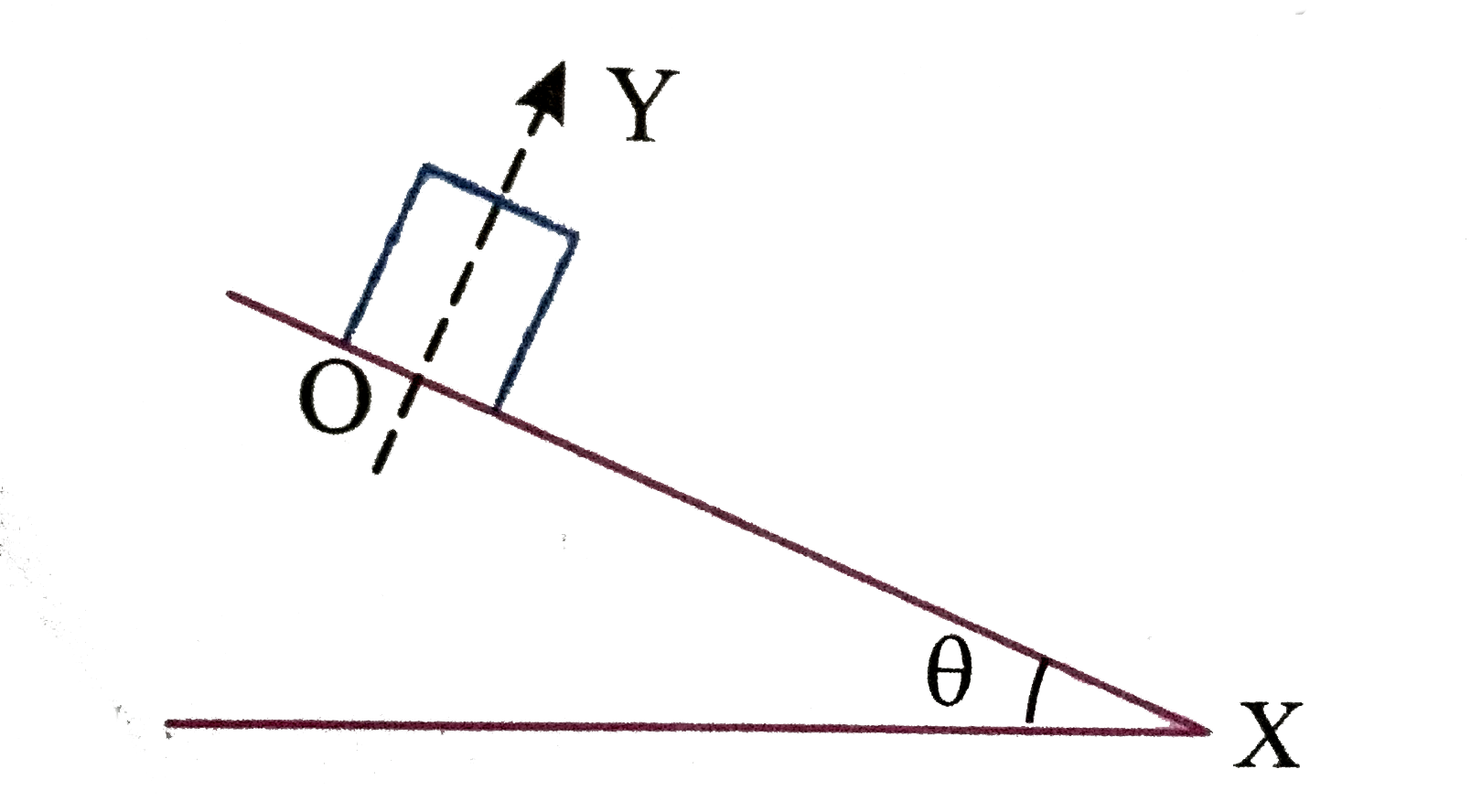
Frictional force acting on the block after it comes to rest:
View SolutionIn the adjacent figure, x-axis has been taken down the inclined plane. The coefficient of friction varies with x as μ=kx, where k=tanθ. A block is released at O
Frictional acting on the block just before it comes to rest :
View SolutionA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .
.
View Solution

