The coefficient of friction between the block and the inclined plane is μ.
The correct Answer is:a=gm−M(sinα±μcosα)m+M
Since the force of sliding friction T is opposite in direction to that of the block.s motion, the result will be essentially dependent on the initial direction of the block velocity. Consider all the possible cases.
Let the initial velocity of teh weight be directed downwards (Fig.). The equations of motion will be of the form
mg−F=ma
F−T−Mgsinα=Ma, where T=μQ=μMgcosα
Hence
a=gm−M(sinα+μcosα)m+M,F=mMg(1+sinα+μcosα)m+M
If m>M(sinα+μcosα), then a>0 and the speed of the system increases. If m<M(sinα+μcosα), then a<0, and the speed
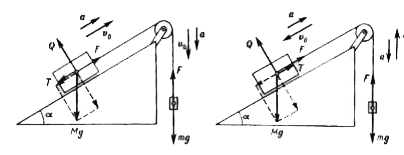
of the system decreases. Lastly, when m=M(sinα+μcosα), we have a = 0, and the system moves at a constant speed.
(2) Let the initial velocity of the weight be directed upwards (Fig.). Then, as may easily be inferred,
a=gm−M(sinα−μcosα)m+M,F=mMg(1+sinα−μcosα)m+M
If m>M(sinα−μcosα), then a>0, and the speed of the system decreases. If m<M(sinα−μcosα), then a<0, and the speed of the system moves at a constant speed.
(3) Finally, let the system be at rest. Then a force of static friction will act between the block and the inclined plane, its direction being dependent on the direction in which the system would move in the absence of friction. If m>Msinα, the block in th absence of friction moves upwards. Therefore the force of static friction is directed downwards, as in Fig. If m<Msinα, the block in the absence of friction moves downwards, and for this reason the force of static friction is directed upwards, as in Fig.
If one analyses the two preceding cases, one can easily see that for m>M(sinα+μcosα) the black will move up the inclined plane with an acceleration, for m<M(sinα−μcosα) it will move down the inclined plane with an acceleration, will for
M(sinα−μcosα)≤m≤M(sinα+μcosα)
the system will remain at rest.
Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
Knowledge Check
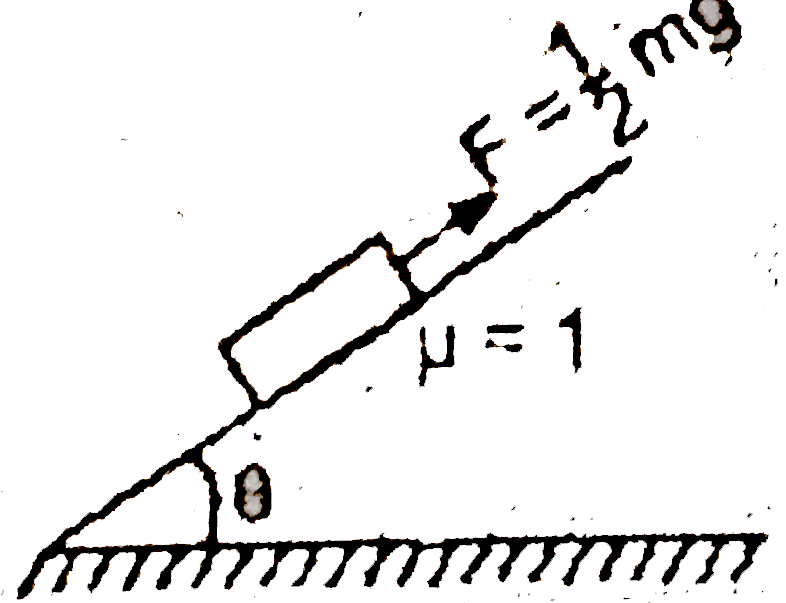
A block of mass 0.1 kg is kept on an inclined plane whose angle of inclination can be varied from θ=30∘ to θ=90∘. The coefficient of friction between the block & the inclined plane is μ=1. A force of constant magnitude 12mg newton always acts on the block directed up the inclined plane and parallel to it. Then :
 A
A B
B C
C D
D
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of theseIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
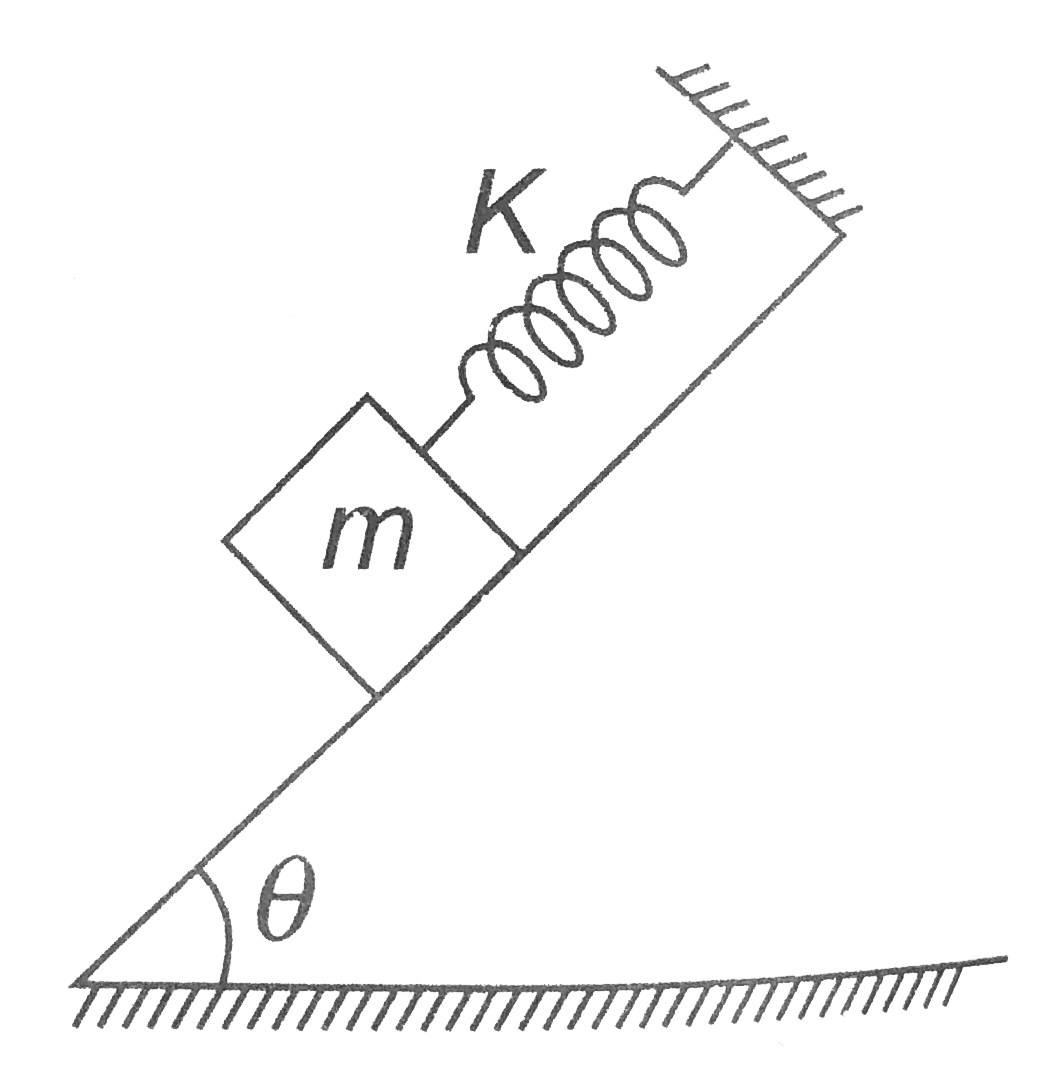 A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.

View SolutionTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?

View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
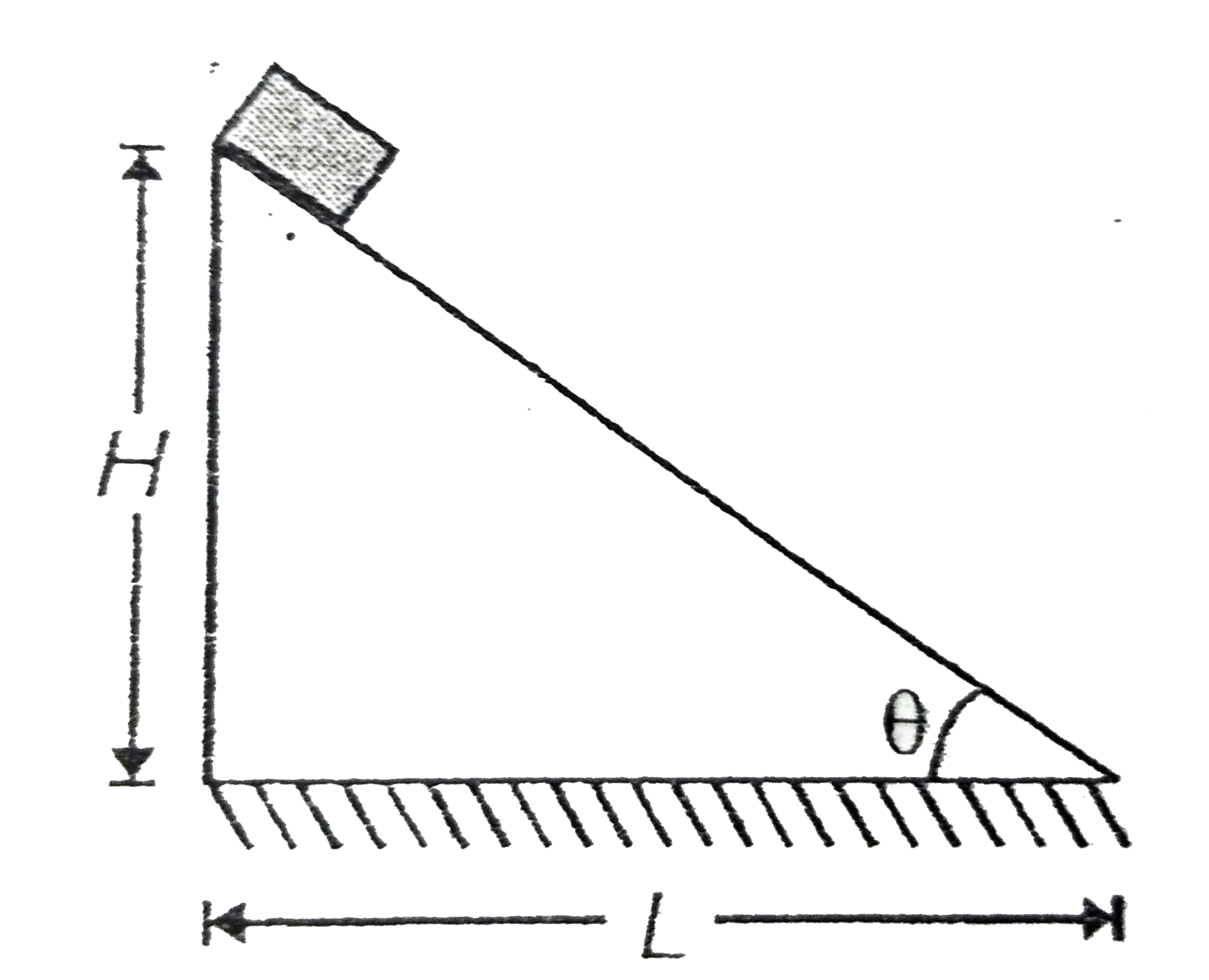
View SolutionTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?

View Solution

