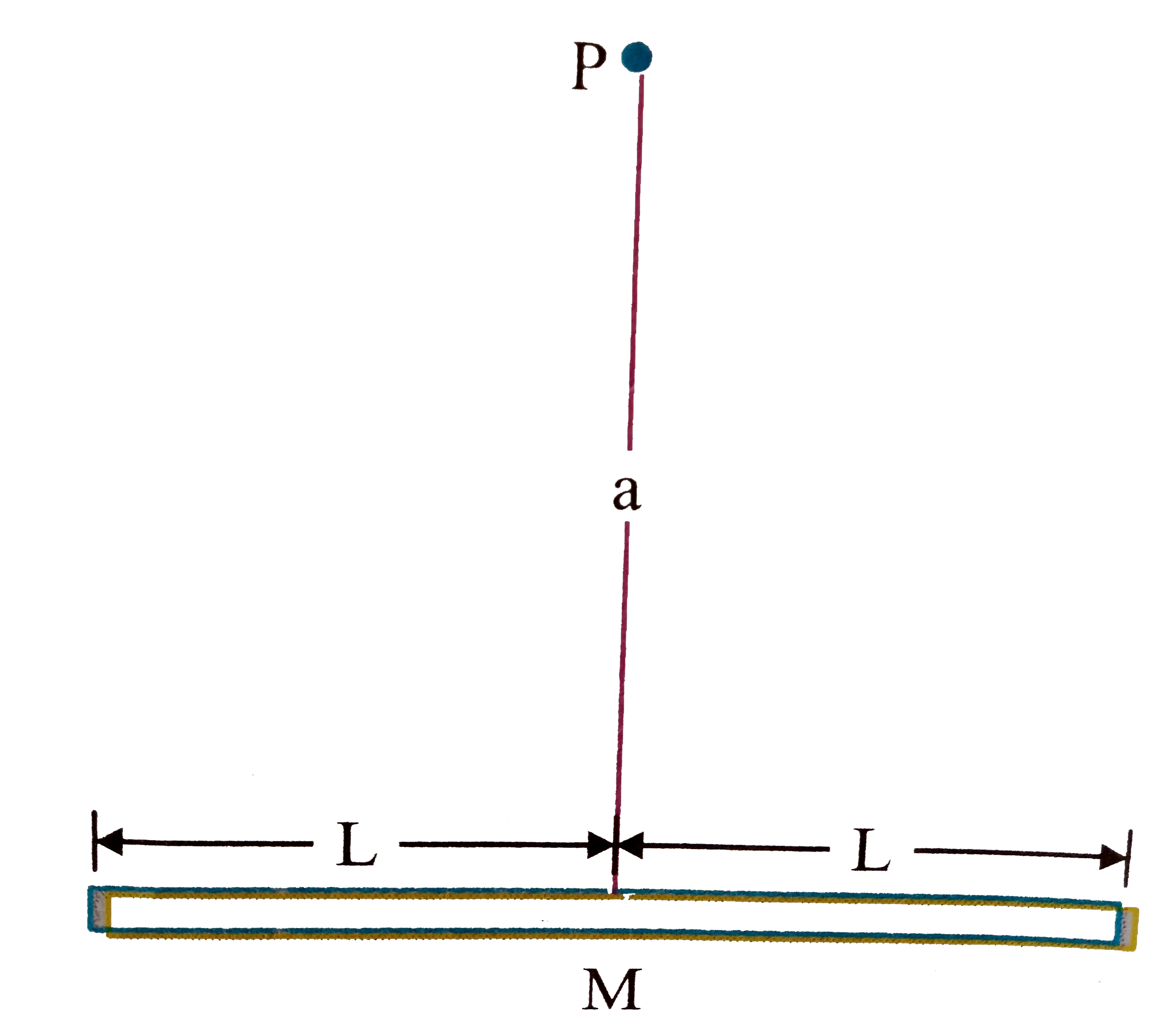
Mass M is distributed uniformly along a line of length 2L. A particle of mass m is at a point that is at a distance a above the centre of the line on the its perpendicular bisector (Point P in figure). The gravitational force that the line exert on the particle is
GMm√L2+a2
GMma(L2+a2)
GMma√L2+a2
GMma(L2+a2)2
The correct Answer is:C
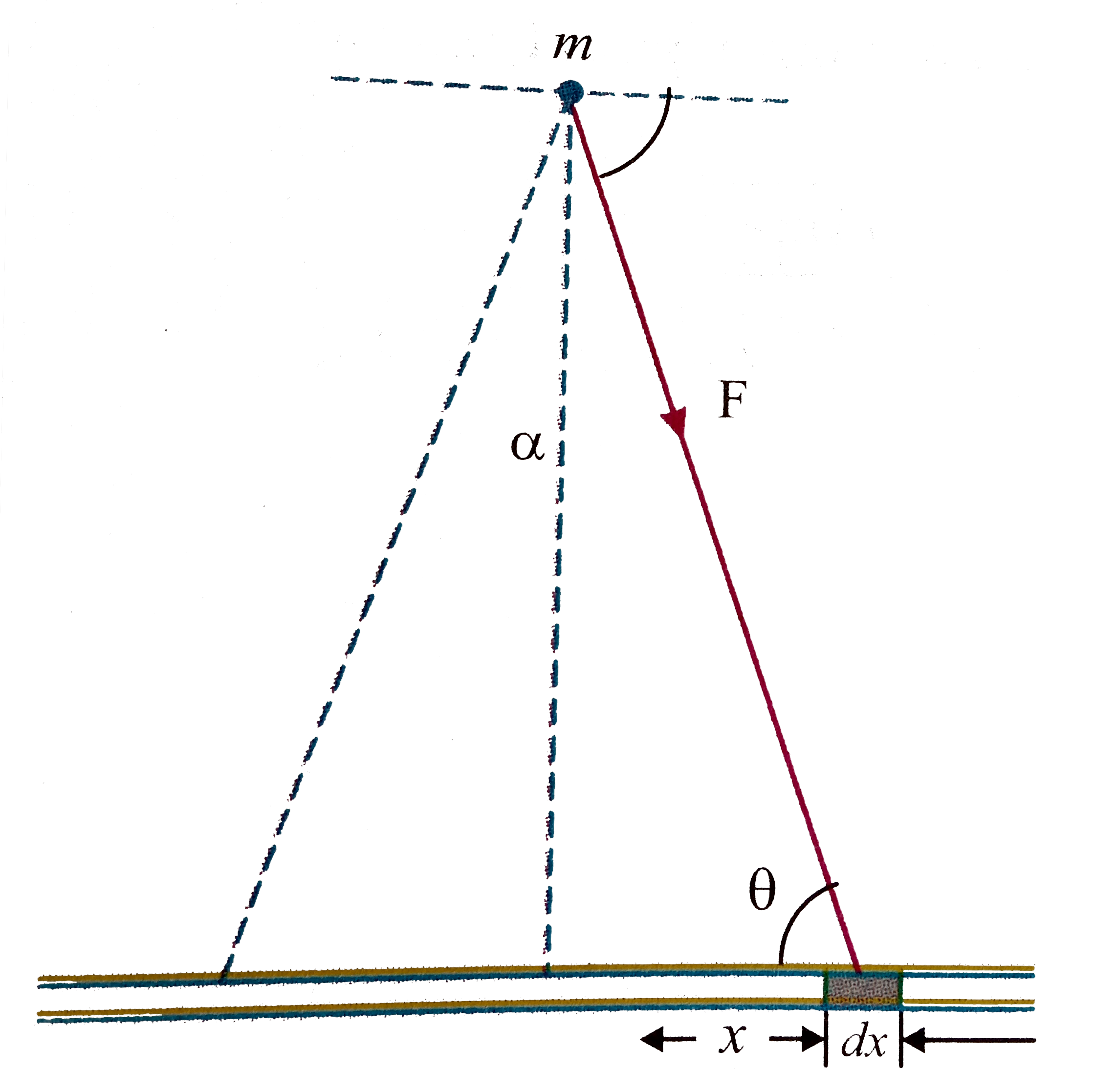
dM=(M2L)dxF=Gm(dM)(a2+x2)
Components Fcosθ (i.e. parallel to line) cancel each other. Net force will be perpendicular to the rod.
F≠t=∫x=Lx=02Fsinθ=∫L02GmM2L(a2+x2)adx(a2+x2)1/2
∫L0GMma.dxL(a2+x2)3/2=GMma√L2+a2
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
A charge Q is distributed over a line of length L Another point charge q is placed at a distance r from the centre of the line distribution.Then the force experienced by q is
View SolutionA charge Q is distributed over a line of length L Another point charge q is placed at a distance r from the centre of the line distribution. Then the force experienced by q is
View Solution
Knowledge Check
A particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
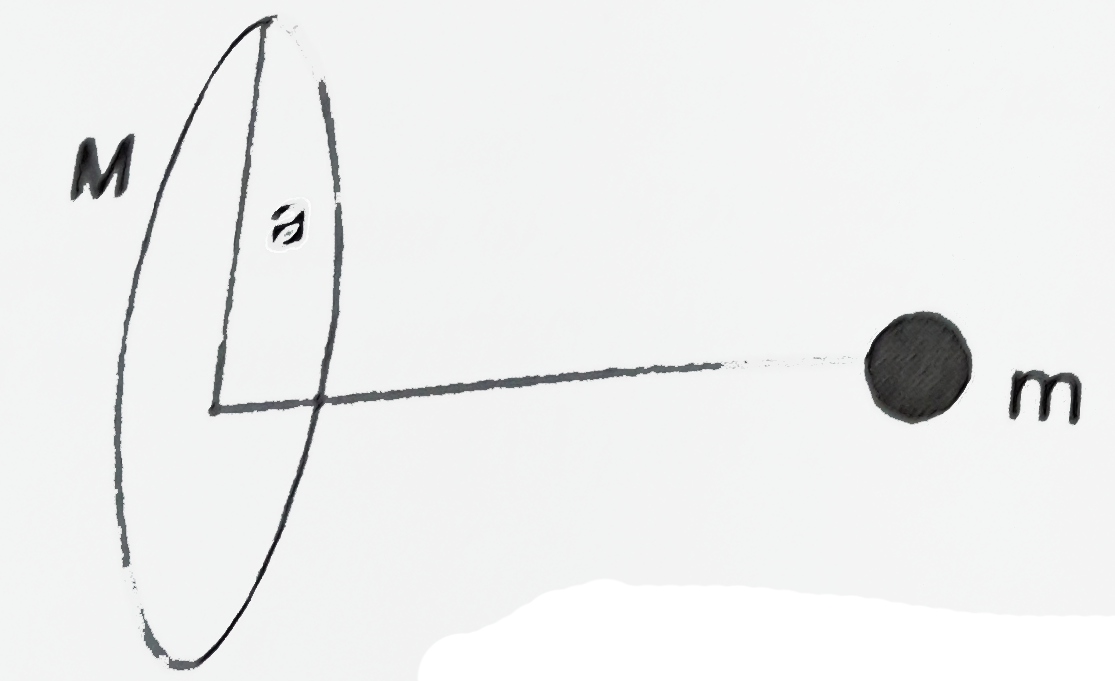
Gravitational potential energy of this system.A−GMm√a2+x2BGMmaCGMmxDNone of theseA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
The force, when x=0 :AGMmx2BGMmx√a2+x2CGMmx(a2+x2)3/2DZeroA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
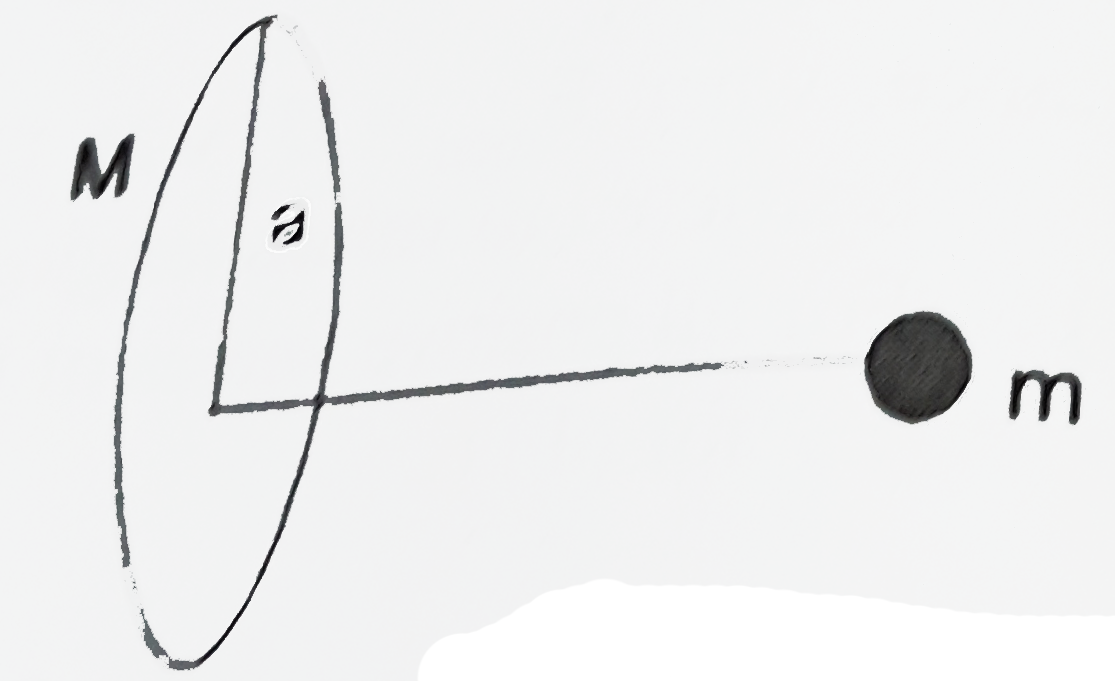
if x<<a, the particle of mass m will:Aperform oscillatory motionBperform S.H.M.CbothDNone
Two stationary particles of masses M1 and M2 are 'd' distance apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from M1 ?
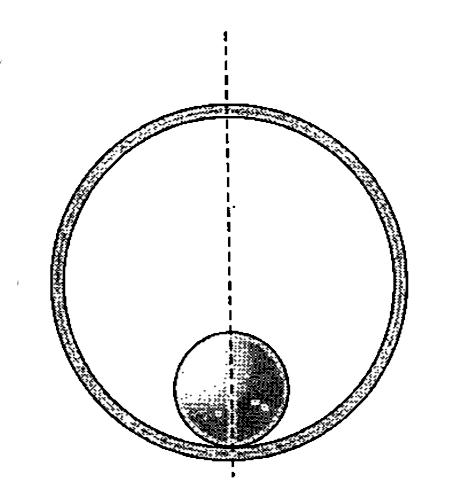
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
View SolutionTwo bodies, each of mass M, are kept fixed with a separation 2L. A particle of mass m is projected from the midpoint of the line joining their centres, perpendicular to the line. The gravitational constant is G. The correct statement (s) is (are)
View SolutionTwo particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
View SolutionThe bodies of mass m and 4m are placed at a distance of 6m apart. P is the point on the line joining two bodies where gravitational field is zero. The gravitational potential at this point is
View Solution

