A larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for m=k(M288). The value of k is
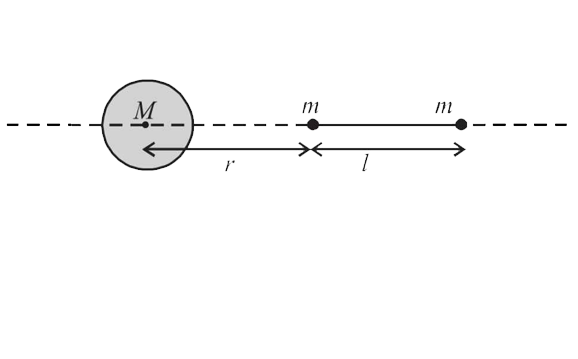
The correct Answer is:7
At the point P the starts, let the gravitational field intensity be zero. So,
G(16M)x2=GM(10a−x)2
⇒x10a−x=4⇒x=−4x+40a⇒x=8a
If means that if the body crosses the point P, it is attracted by the other star. thus the critical velocity is the velocity of the body just to reach the point P, which can be given as
(ΔV)=12mv2, where ΔV=potential differences between A and P
⇒ΔV=|Potential at A-Potential at P|
=(G(16M)2a−GM8a)−(−G(16M)8a)+GM2a)
45GM8a,V=√2(ΔV)=√90GM8a=√45GM4a
=32√GMa=3×2.4142×√GMa
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Find the potential V at P in the gravitational field of fixed point mass M.
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
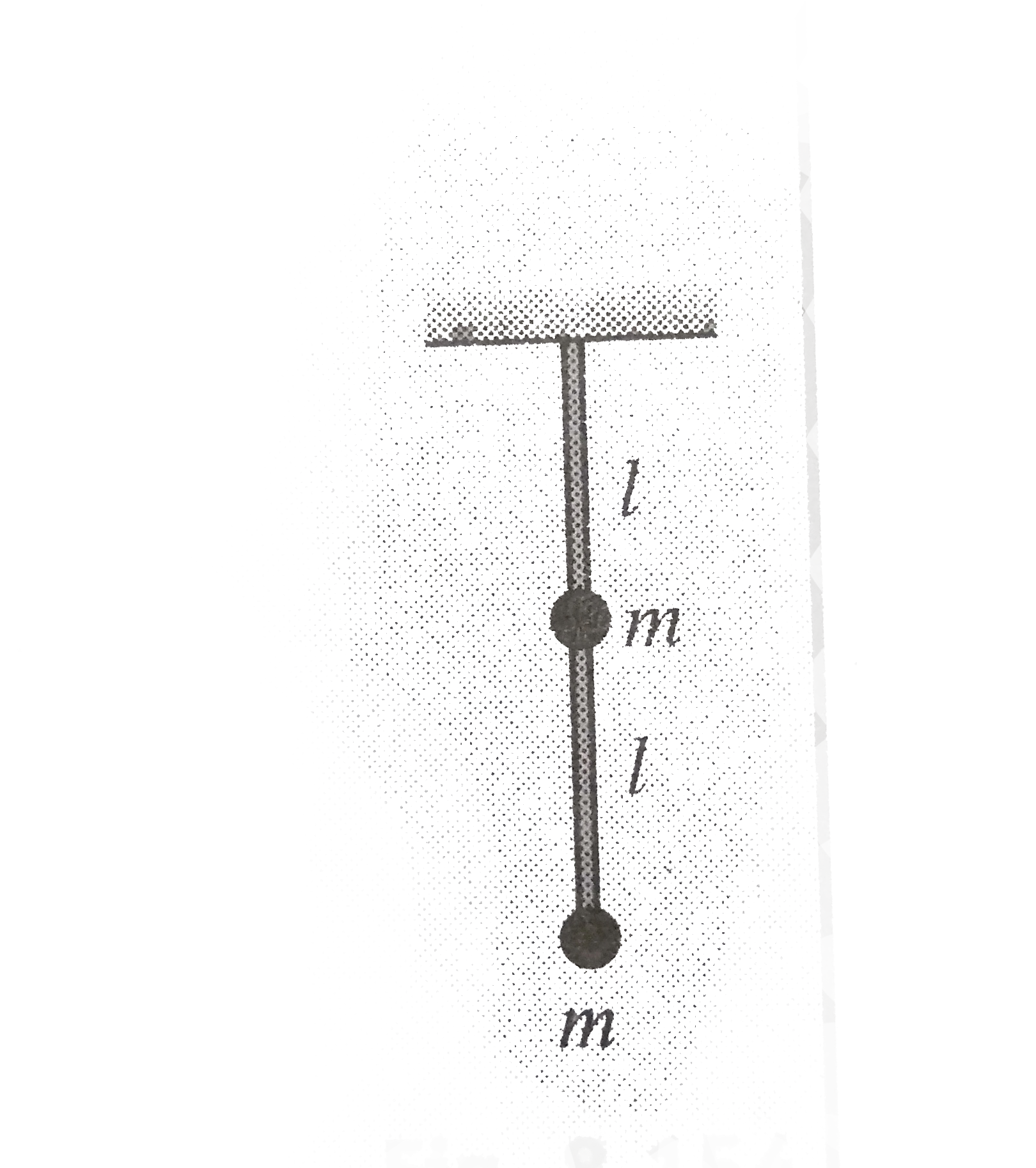
View Solution
Knowledge Check
Two particles of masses m1 and m2 are connected to a rigid massless rod of length r to constitute a dumb bell which is free to move in the plane. The moment of inertia of the dumb bell about an axis perpendicular to the plane passing through the centre of mass is
Am1m2r2m1+m2B(m1+m2)r2Cm1m2r2m1−m2D(m1−m2)r2Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)A system consists of two masses connected by a massless rod lies along x-axis. The distance of centre of mass from O is
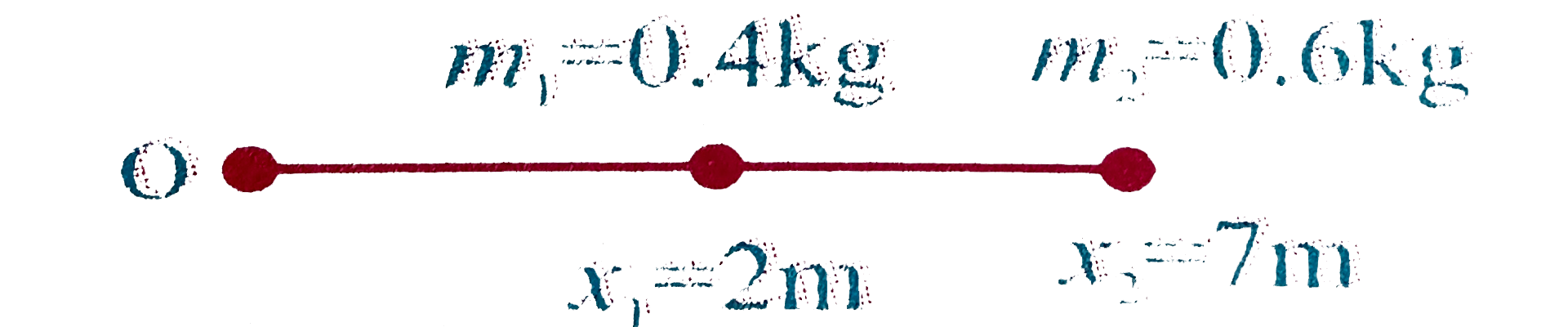 A2mB3mC5mD7m
A2mB3mC5mD7m
Two point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionA point mass is placed at a distance a from one end of a rod of mass M and length l on the line which passes through the central axis of the rod. The potential energy of the system.
View SolutionTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View SolutionMoment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
View Solution

