Find the speeds of a planet of mass m in its perihelion and aphelion postitions. The semimajor axis of its orbit is a, ecentricity is e and te mass of the sun is M. Also find the total energy of the planet in terms of the given parameters.
The correct Answer is:A, B
Let υ1 and υ2 be the speeds of the planet at perihelion and aphelion positions.
r1=a(1−e)
and r2=a(1+e) ..(i)

Applying conservation of momentum of the planet at p (perihelion) and A (aphelion)
mυ1r1sin90∘=mυ2r2sin90∘
υ1r1=υ2r2
Applying conservation of mechanical energy in these two positions, we have
12mυ21−GMmr1=12mυ22−GMmr2
Solving Eqs. (i), (ii) and (iii), we get
υ1=√GMa(1+e1−e) υ2=√GMa(1−e1+e)
Further, total energy of the planet
E=12mυ21−GMmr1=12m[GMa(1−e1+e)]−GMma(1−e)
=GMma(1−e)[(1+e2)−1]
=GMma(1−e)(e−12) or E=−GMm2a
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.2
9 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Solved Examples
16 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Find the speeds of a planet of mass m in its perihelion and aphelion postitions. The semimajor axis of its orbit is a, ecentricity is e and te mass of the sun is M. Also find the total energy of the planet in terms of the given parameters.
View SolutionA planet of mass m is revolving around the sun in an elliptical orbit. The minimum and maximum distances of the planet from the sun are s1 and s2. Derive the relation between time period of the planet in terms of s1 and s2.
View Solution
Knowledge Check
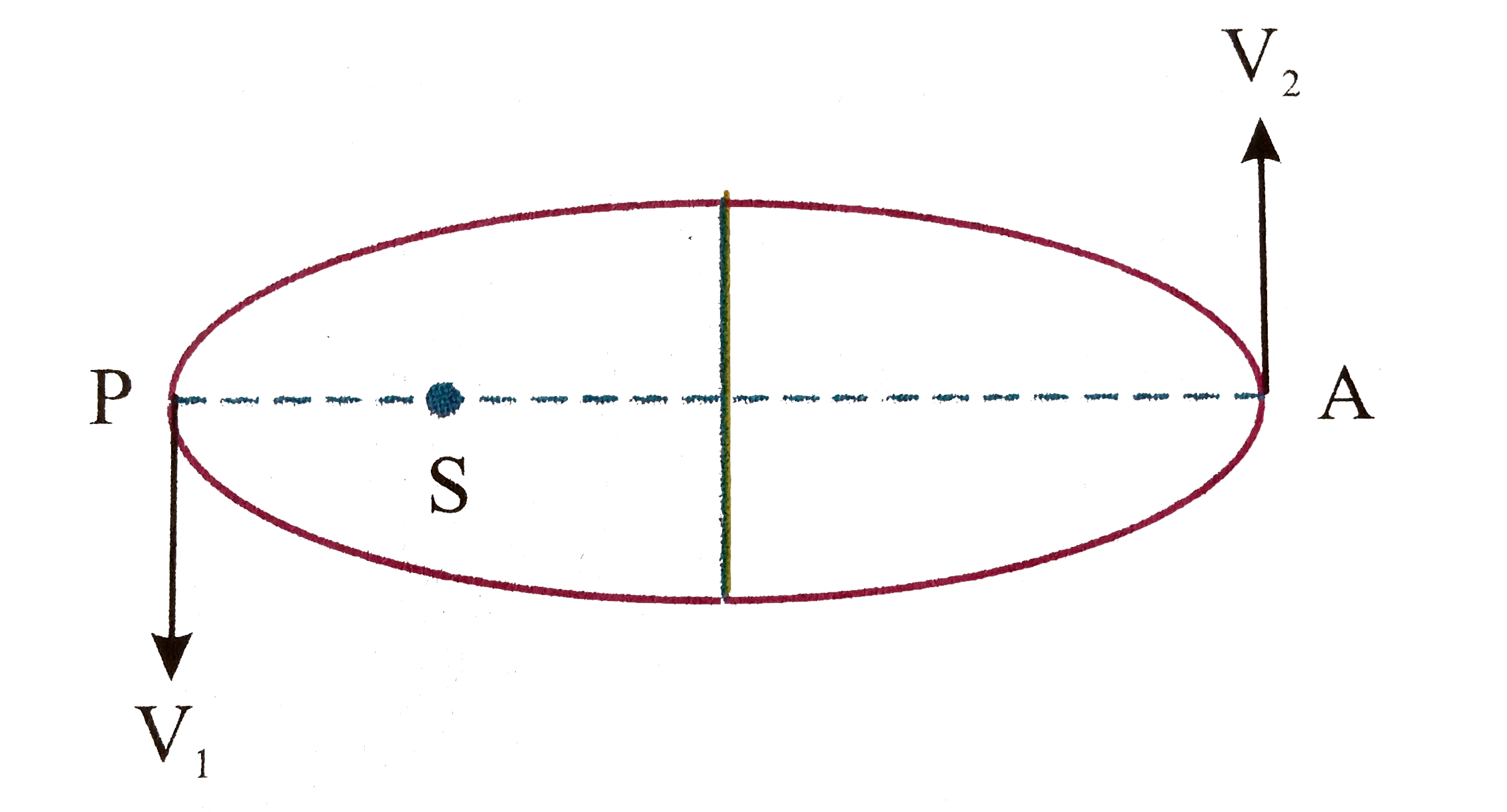
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.A−GMm4aB−GMm22aC−GMm8aD−GMm2aA planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusion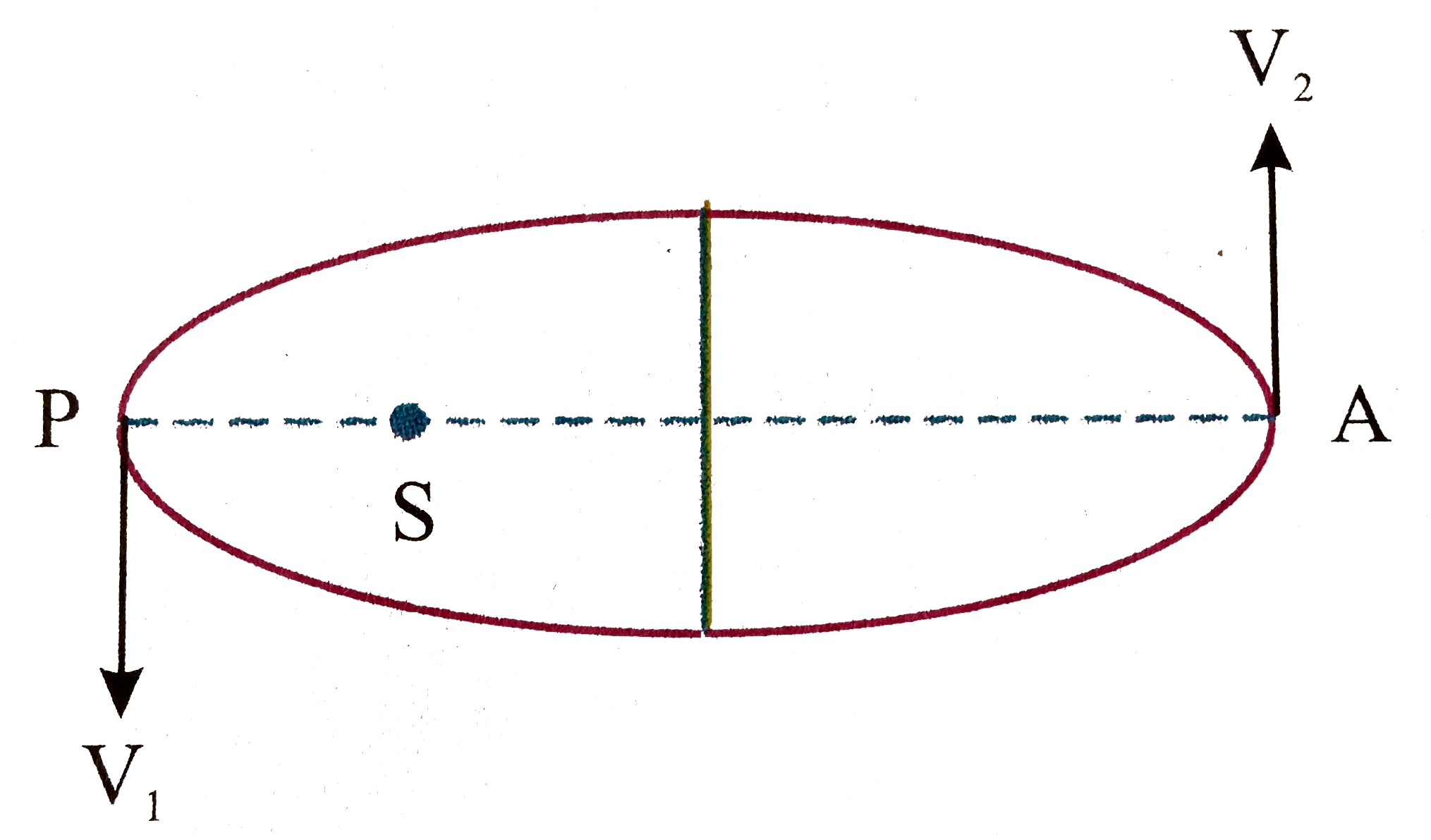
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.A√GMa(1+e)(1−e)B√GMa(1−e)(1+e)C√GMa3(1+e2)(1−e2)D√GMa3(1−e2)(1+e2)
A plant of mass m1 revolves round the sun of mass m2. The distance between the sun the planet is r. Considering the motion of the sun find the total energy of the system assuming the orbits to be circular.
View Solution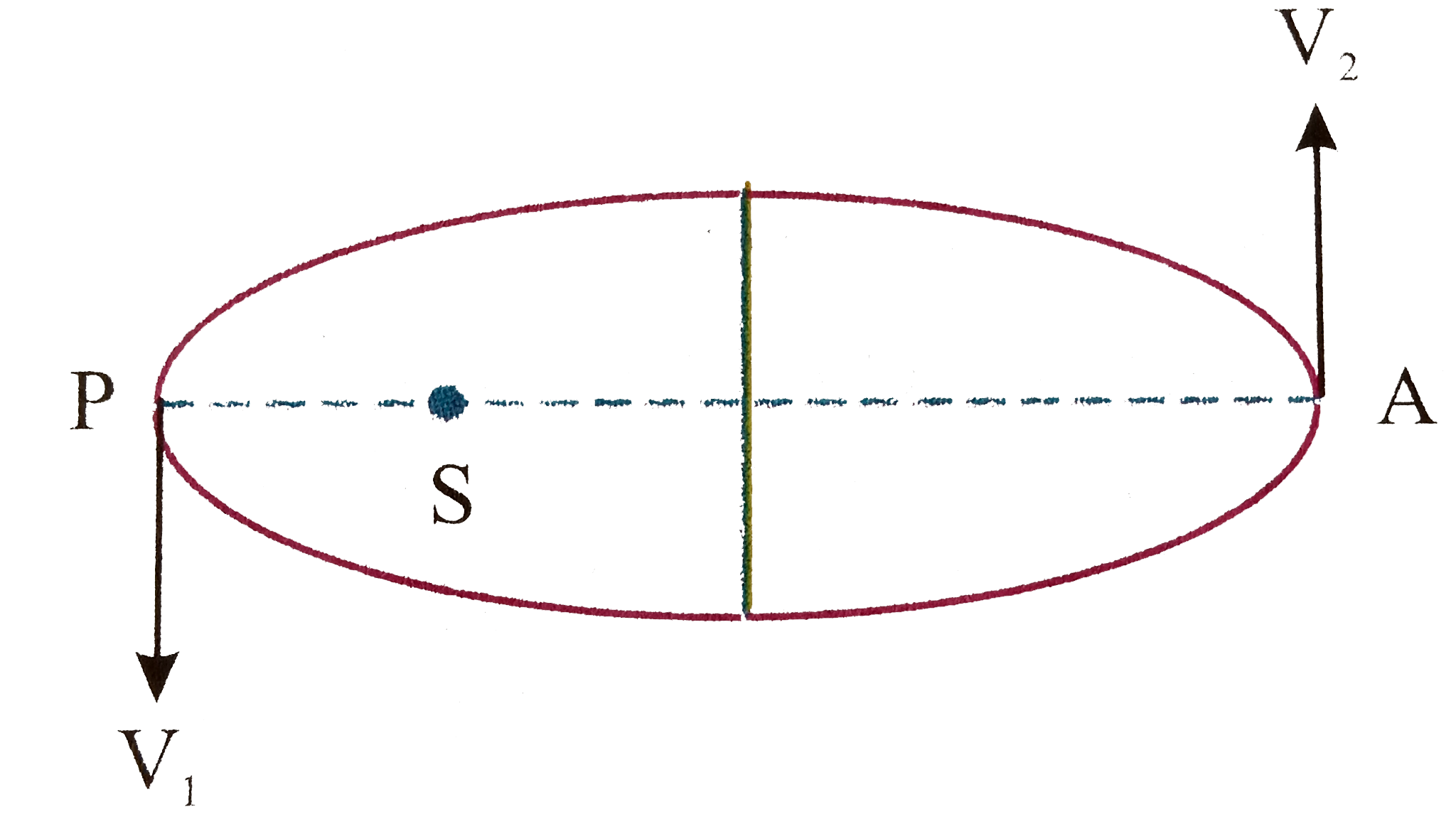
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
View SolutionThe ratio of kinetic energy of a planet at perigee and apogee during its motion around the sun in eliptical orbit of ecentricity e is
View SolutionIf a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View Solution
