From a uniform circular disc of diameter circular disc of diameter and having centre at a distance from the centre of the disc is scooped out. Determine the centre of mass of remaining portion.
To determine the center of mass of the remaining portion of a uniform circular disc after scooping out a smaller disc, we can follow these steps:
Step 1: Define the Parameters
- Let the diameter of the larger disc be d. Therefore, its radius R is given by:
R=d2
- The diameter of the smaller disc being scooped out is d6, which means its radius rs is:
rs=d12
Step 2: Calculate the Masses
- The mass of the larger disc m can be expressed in terms of its area and density σ:
m=σ⋅Area of larger disc=σ⋅πR2=σ⋅π(d2)2=σπd24
- The area of the smaller disc is:
Area of smaller disc=πr2s=π(d12)2=πd2144
- Thus, the mass of the smaller disc ms is:
ms=σ⋅Area of smaller disc=σ⋅πd2144
Step 3: Calculate the Remaining Mass
- The mass of the remaining portion of the larger disc mr is:
mr=m−ms=σπd24−σπd2144
- To simplify this, find a common denominator:
mr=σπd2(36144−1144)=σπd2⋅35144
Step 4: Determine the Position of the Smaller Disc
- The center of the smaller disc is located at a distance of d4 from the center of the larger disc.
Step 5: Use the Center of Mass Formula
- The center of mass xcm of the system can be calculated using the formula:
xcm=mr⋅xr−ms⋅xsmr−ms
where:
- xr is the position of the center of mass of the remaining disc (unknown),
- xs=d4 is the position of the center of the smaller disc.
Step 6: Set Up the Equation
- Since the total mass of the system is zero (as we are considering the center of mass relative to the larger disc):
0=mr⋅xr−ms⋅d4
Rearranging gives:
mr⋅xr=ms⋅d4
Step 7: Substitute the Masses
- Substitute mr and ms:
(35σπd2144)xr=(σπd2144)⋅d4
Step 8: Solve for xr
- Cancel σπd2 from both sides:
35xr=d4
- Therefore, solving for xr:
xr=d4⋅35=d140
Step 9: Determine the Final Position
- Since the smaller disc is scooped out, the center of mass will be shifted towards the larger disc. Thus, the center of mass of the remaining portion is:
xcm=−d140
Final Answer
The center of mass of the remaining portion of the disc is located at:
−d140
- Let the diameter of the larger disc be d. Therefore, its radius R is given by:
R=d2
- The diameter of the smaller disc being scooped out is d6, which means its radius rs is:
rs=d12
- The mass of the larger disc m can be expressed in terms of its area and density σ:
m=σ⋅Area of larger disc=σ⋅πR2=σ⋅π(d2)2=σπd24
- The area of the smaller disc is:
Area of smaller disc=πr2s=π(d12)2=πd2144
- Thus, the mass of the smaller disc ms is:
ms=σ⋅Area of smaller disc=σ⋅πd2144
- The mass of the remaining portion of the larger disc mr is:
mr=m−ms=σπd24−σπd2144
- To simplify this, find a common denominator:
mr=σπd2(36144−1144)=σπd2⋅35144
- The center of the smaller disc is located at a distance of d4 from the center of the larger disc.
- The center of mass xcm of the system can be calculated using the formula:
xcm=mr⋅xr−ms⋅xsmr−ms
where:
- xr is the position of the center of mass of the remaining disc (unknown),
- xs=d4 is the position of the center of the smaller disc.
- Since the total mass of the system is zero (as we are considering the center of mass relative to the larger disc):
0=mr⋅xr−ms⋅d4
Rearranging gives:
mr⋅xr=ms⋅d4
- Substitute mr and ms:
(35σπd2144)xr=(σπd2144)⋅d4
- Cancel σπd2 from both sides:
35xr=d4
- Therefore, solving for xr:
xr=d4⋅35=d140
- Since the smaller disc is scooped out, the center of mass will be shifted towards the larger disc. Thus, the center of mass of the remaining portion is:
xcm=−d140
The center of mass of the remaining portion of the disc is located at:
−d140
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:VALUE BASED QUESTIONS
Explore 5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:CURIOSITY QUESTIONS
Explore 4 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
From a uniform circular disc of diameter D, a circular disc or hole of diameter D/6 and having its centre at a distance of D/4 from the centre of the disc is scopped out. Determine the centre of mass of the remaining portion.
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View Solution
Knowledge Check
A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)A circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by
 A5cmB9cmC4.5cmD5.5cm
A5cmB9cmC4.5cmD5.5cm
A circular disc of radius R4 is cut from a uniform circular disc of radius R.
The centre of cut portion is at a distance of R2 from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionFind the centre of mass of the shaded portion of a disc
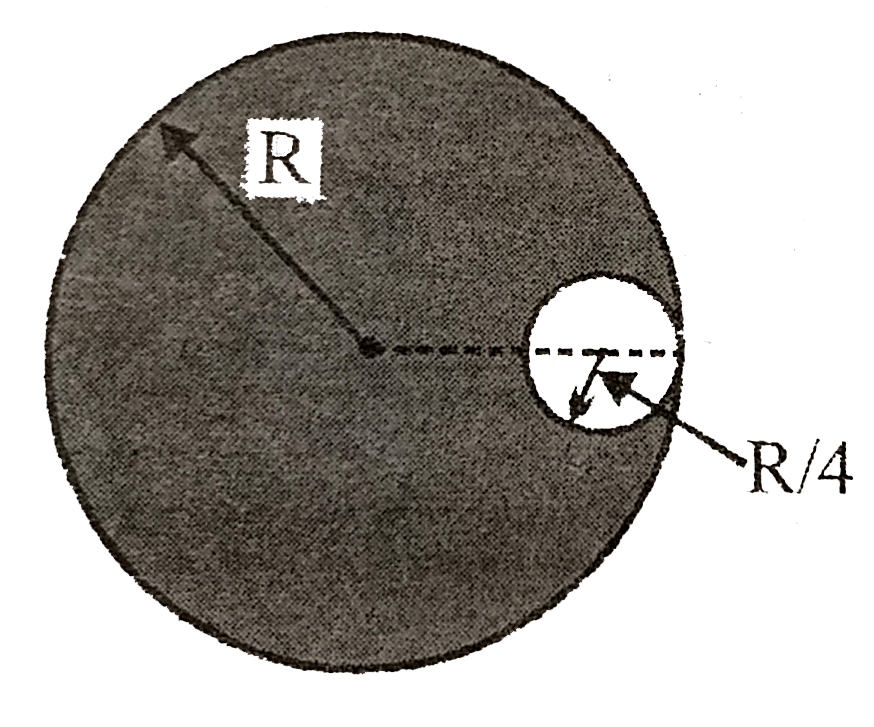
View SolutionFind the centre of mass of the shaded portion of a disc.
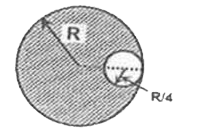
View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View Solution

