From a uniform disc of radius , a circular section of radius is cut out. The centre of the hole is at from the centre of the original disc. Locate the centre of mass of the resulating flat body.
To find the center of mass of the resulting flat body after cutting out a circular section from a uniform disc, we can follow these steps:
Step 1: Understand the Configuration
We have a uniform disc of radius R and we cut out a smaller disc of radius R2 from it. The center of the smaller disc is located at a distance R2 from the center of the original disc.
Step 2: Define the Masses
Let the mass of the original disc be m. Since the disc is uniform, the mass per unit area σ is constant. The area of the original disc is A=πR2, so we can express the mass as:
m=σ⋅A=σ⋅πR2
The area of the cut-out disc (hole) with radius R2 is:
Ahole=π(R2)2=πR24
Thus, the mass of the hole is:
mhole=σ⋅Ahole=σ⋅πR24=m4
Step 3: Calculate the Mass of the Remaining Disc
The mass of the remaining part of the disc is:
mremaining=m−mhole=m−m4=3m4
Step 4: Identify the Centers of Mass
- The center of mass of the original disc is at the origin (0, 0).
- The center of mass of the hole is at (R2,0).
- The center of mass of the remaining disc (which we need to find) will be at some position x along the x-axis.
Step 5: Use the Center of Mass Formula
For a system of particles, the center of mass xcm can be calculated using:
xcm=m1x1+m2x2m1+m2
Here:
- m1=3m4 (mass of the remaining disc) at position x
- m2=m4 (mass of the hole) at position R2
Setting the total mass equal to m:
0=3m4⋅x+m4⋅R2m
This simplifies to:
0=3x4+R8
Step 6: Solve for x
Multiplying through by 8 to eliminate the fraction:
0=6x+R
Rearranging gives:
6x=−R⇒x=−R6
Conclusion
The center of mass of the resulting flat body (remaining disc) is located at:
Center of Mass=(−R6,0)
We have a uniform disc of radius R and we cut out a smaller disc of radius R2 from it. The center of the smaller disc is located at a distance R2 from the center of the original disc.
Let the mass of the original disc be m. Since the disc is uniform, the mass per unit area σ is constant. The area of the original disc is A=πR2, so we can express the mass as:
m=σ⋅A=σ⋅πR2
Ahole=π(R2)2=πR24
Thus, the mass of the hole is:
mhole=σ⋅Ahole=σ⋅πR24=m4
The mass of the remaining part of the disc is:
mremaining=m−mhole=m−m4=3m4
- The center of mass of the original disc is at the origin (0, 0).
- The center of mass of the hole is at (R2,0).
- The center of mass of the remaining disc (which we need to find) will be at some position x along the x-axis.
For a system of particles, the center of mass xcm can be calculated using:
xcm=m1x1+m2x2m1+m2
Here:
- m1=3m4 (mass of the remaining disc) at position x
- m2=m4 (mass of the hole) at position R2
0=3m4⋅x+m4⋅R2m
This simplifies to:
0=3x4+R8
Multiplying through by 8 to eliminate the fraction:
0=6x+R
Rearranging gives:
6x=−R⇒x=−R6
The center of mass of the resulting flat body (remaining disc) is located at:
Center of Mass=(−R6,0)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:QUESTIONS
Explore 15 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADVANCED PROBLEMS FOR COMPETITIONS
Explore 20 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
From a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA circular section of radius r si cut out of a uniform disc of radius R, the centre of the hole being R/2 from the centre of the original disc. Locate the centre of gravity of the remainder.
View Solution
Knowledge Check
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
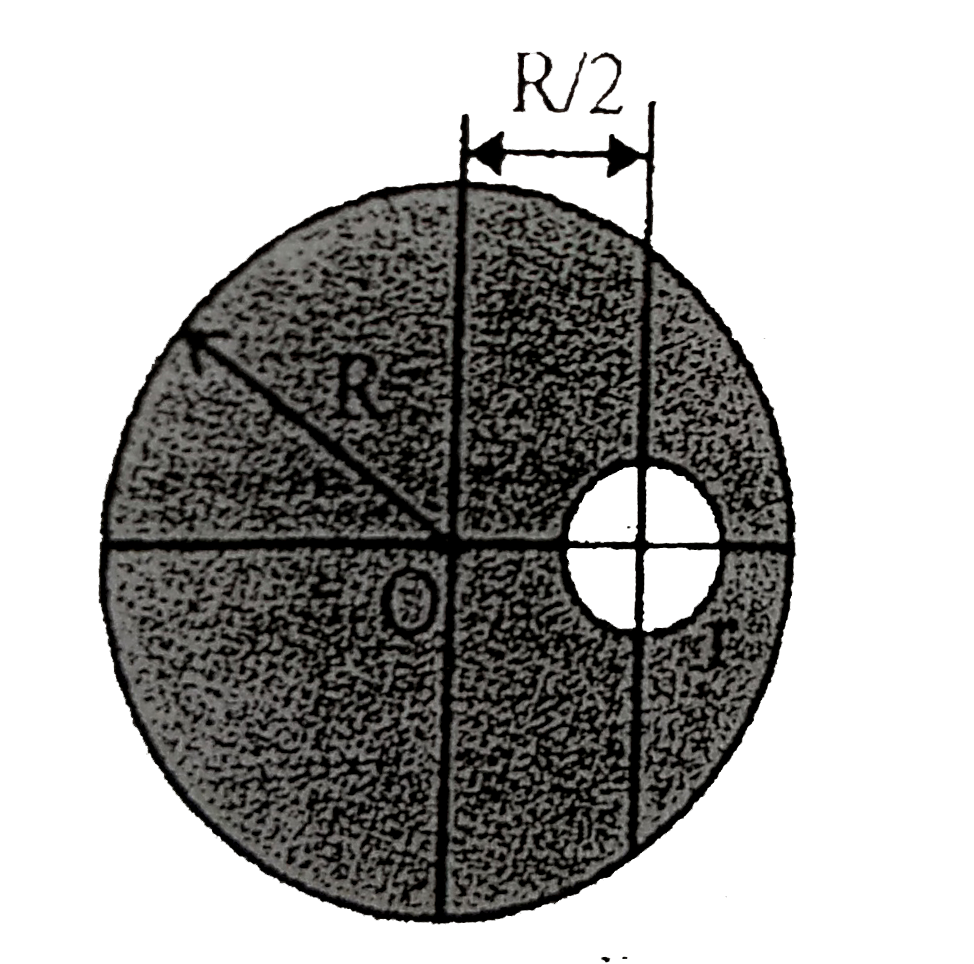 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
From a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View SolutionFind the centre of mass of a unifrom disc of radius a from which a circulr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
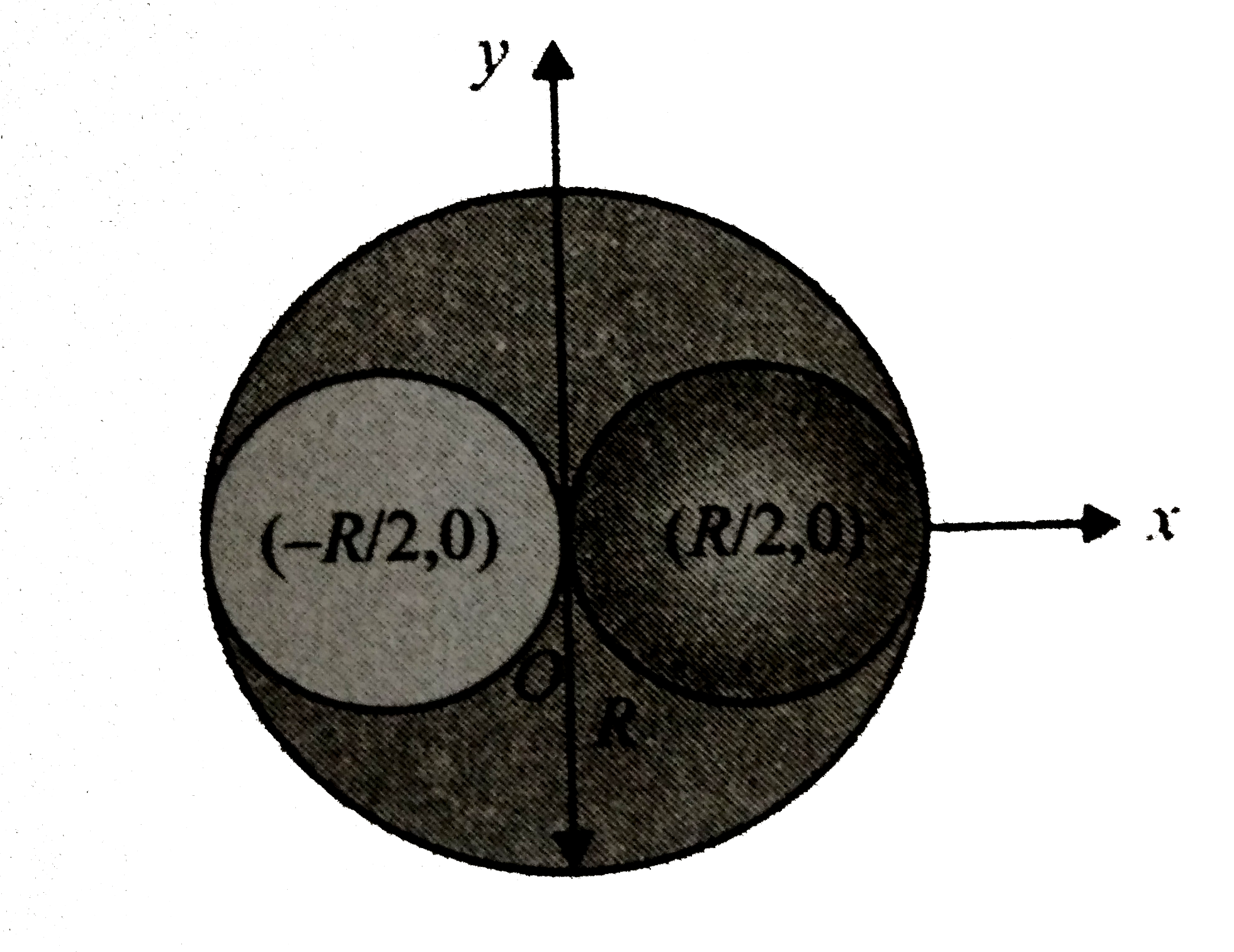
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
View SolutionA circular disc of radius R4 is cut from a uniform circular disc of radius R.
The centre of cut portion is at a distance of R2 from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View Solution