Find the centre of mass of $a$ unifrom disc of radius a from which a circulr section of radius $b$ has been removed. The centre of hole is at a distance $c$ from the centre of the disc.

Video Solution

Text Solution

Verified by Experts

Suppose the circular disc of radius a with centre $O$ is made up of
(i) circular section of radius b with centre $O_{1}$ and (ii) remaining portion of disc with c.m at $O_{2}$ .
Taking $O$ as origin, and $O_{1}, O_{2}$ on X-axis, $(y = 0, z = 0)$ , Fig. the position of c.m of disc is given by
$x_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}}$ ..(i)
If $σ$ is surface density of material of the disc,
$m_{1} = π b^{2} σ, x_{1} = c$
$m_{2} = π (a^{2} - b^{2}) σ$
$x_{2} = ?$
$m_{1} + m_{2} = π a^{2} σ$
From (i), $0 = \frac{π b^{2} σ \times c + π (a^{2} - b^{2}) σ \times x_{2}}{π a^{2} σ} ∴ x_{2} = \frac{- c b^{2}}{(a^{2} - b^{2})}$
Hence c.m of rest of the portion of the disc lies on the left of $O$ , at a distance $x_{2}$ as shown in the Fig.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.

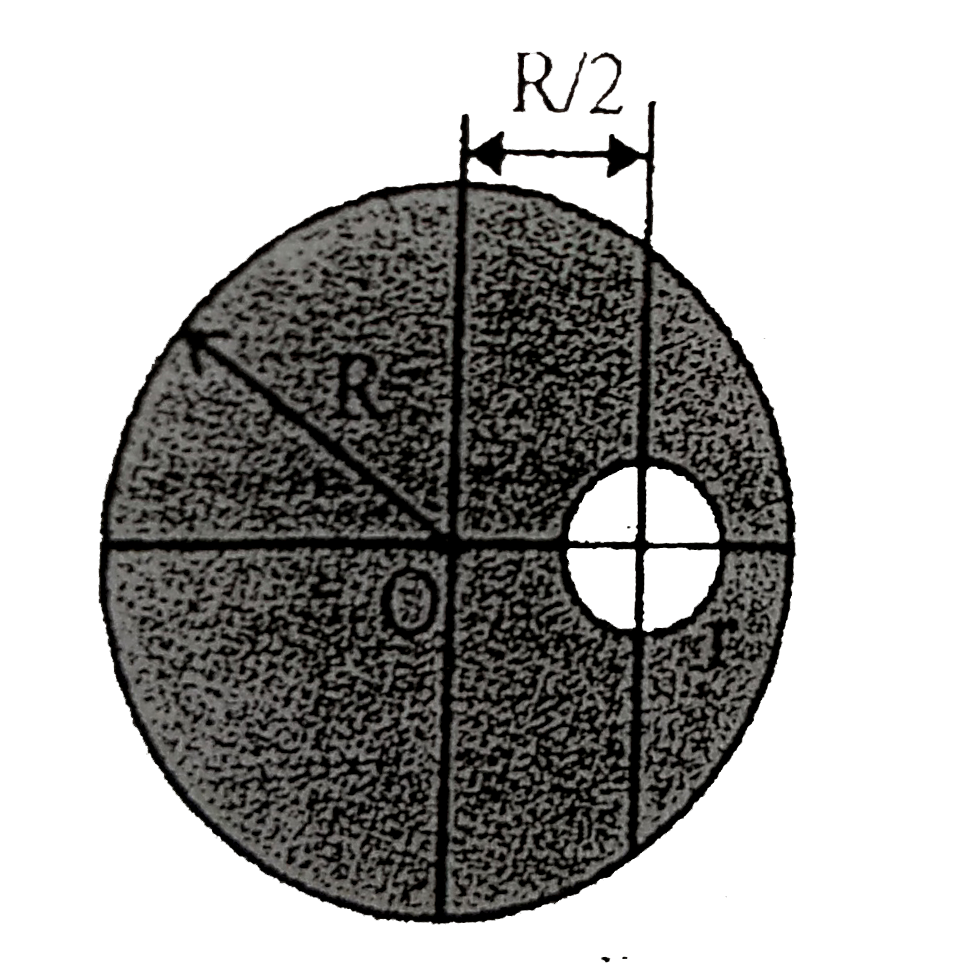A $\frac{R r^{2}}{2 (R^{2} - r^{2})}$ towards right of O
B $\frac{R r^{2}}{2 (R^{2} - r^{2})}$ towards left of O
C $\frac{2 R r^{2}}{(R^{2} + r^{2})}$ towards right of O
D $\frac{2 R r^{2}}{(R^{2} + r^{2})}$ towards left of O
Question 2 - Select One
A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance $x_{2}$ of the center of mass of the remaining part from the initial center of mass O is given by

A $\frac{π b^{2}}{(a^{2} - b^{2})}$
B $\frac{- c b^{2}}{(a^{2} - b^{2})}$
C $\frac{π c^{2}}{(a^{2} - b^{2})}$
D $\frac{π a^{2}}{(c^{2} - b^{2})}$
Question 3 - Select One
A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance $x_{2}$ of the center of mass of the remaining part from the initial center of mass O is given by

A $\frac{π b^{2}}{a^{2} - c^{2}}$
B $\frac{c b^{2}}{a^{2} - b^{2}}$
C $\frac{π c^{2}}{a^{2} - b^{2}}$
D $\frac{c a^{2}}{(c^{2} - b^{2})}$

PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-QUESTIONS

Home
Ask Doubt
Profile