Find the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
The correct Answer is:4R3π
To find the center of mass of a thin uniform disc of radius R from which a small concentric disc of radius r is cut out, we can follow these steps:
Step 1: Define the Discs and Their Masses
Let:
- The mass of the larger disc (radius R) be M.
- The mass of the smaller disc (radius r) be m.
Step 2: Set Up the Coordinate System
Assume a coordinate system where the center of both discs is at the origin (0, 0). This is a symmetric arrangement.
Step 3: Determine the Center of Mass of Each Disc
For a uniform disc, the center of mass is located at its geometric center. Therefore:
- The center of mass of the larger disc (Disc 1) is at (x1,y1)=(0,0).
- The center of mass of the smaller disc (Disc 2) is also at (x2,y2)=(0,0).
Step 4: Apply the Center of Mass Formula
The center of mass (xcm,ycm) of the combined system can be calculated using the formula:
xcm=m1x1+m2x2m1+m2
ycm=m1y1+m2y2m1+m2
Here, m1 is the mass of the larger disc, and m2 is the mass of the smaller disc (which we consider as negative since it is removed).
Step 5: Substitute the Values
Substituting the values into the formulas:
- For the x-coordinate:
xcm=M⋅0+(−m)⋅0M−m=0M−m=0
- For the y-coordinate:
ycm=M⋅0+(−m)⋅0M−m=0M−m=0
Step 6: Conclusion
Thus, the center of mass of the remaining shape after cutting out the smaller disc is:
(xcm,ycm)=(0,0)
Final Answer
The center of mass of the remaining disc is at the origin (0,0).
---
Let:
- The mass of the larger disc (radius R) be M.
- The mass of the smaller disc (radius r) be m.
Assume a coordinate system where the center of both discs is at the origin (0, 0). This is a symmetric arrangement.
For a uniform disc, the center of mass is located at its geometric center. Therefore:
- The center of mass of the larger disc (Disc 1) is at (x1,y1)=(0,0).
- The center of mass of the smaller disc (Disc 2) is also at (x2,y2)=(0,0).
The center of mass (xcm,ycm) of the combined system can be calculated using the formula:
xcm=m1x1+m2x2m1+m2
ycm=m1y1+m2y2m1+m2
Here, m1 is the mass of the larger disc, and m2 is the mass of the smaller disc (which we consider as negative since it is removed).
Substituting the values into the formulas:
- For the x-coordinate:
xcm=M⋅0+(−m)⋅0M−m=0M−m=0
- For the y-coordinate:
ycm=M⋅0+(−m)⋅0M−m=0M−m=0
Thus, the center of mass of the remaining shape after cutting out the smaller disc is:
(xcm,ycm)=(0,0)
The center of mass of the remaining disc is at the origin (0,0).
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I
Explore 45 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)
Explore 2 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Numerical)
Explore 8 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
Figure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.

View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View Solution
Knowledge Check
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
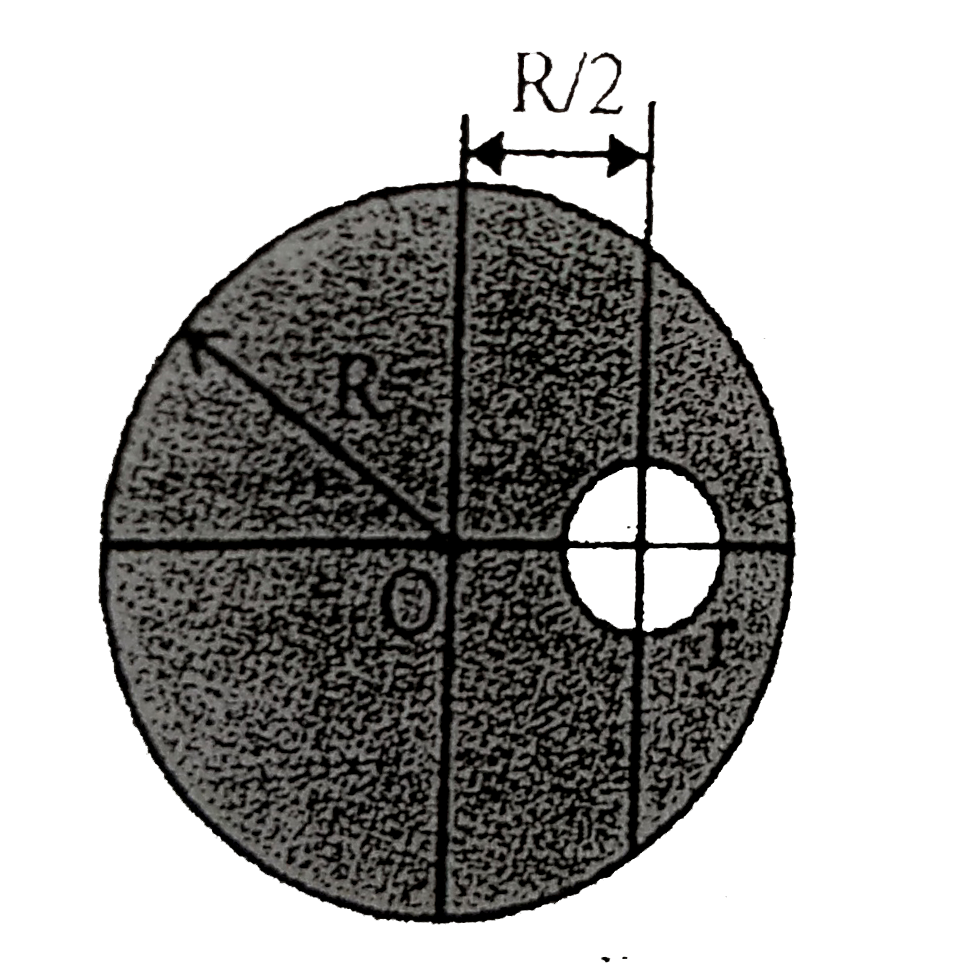 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius a2 is cut from disc of radius a.
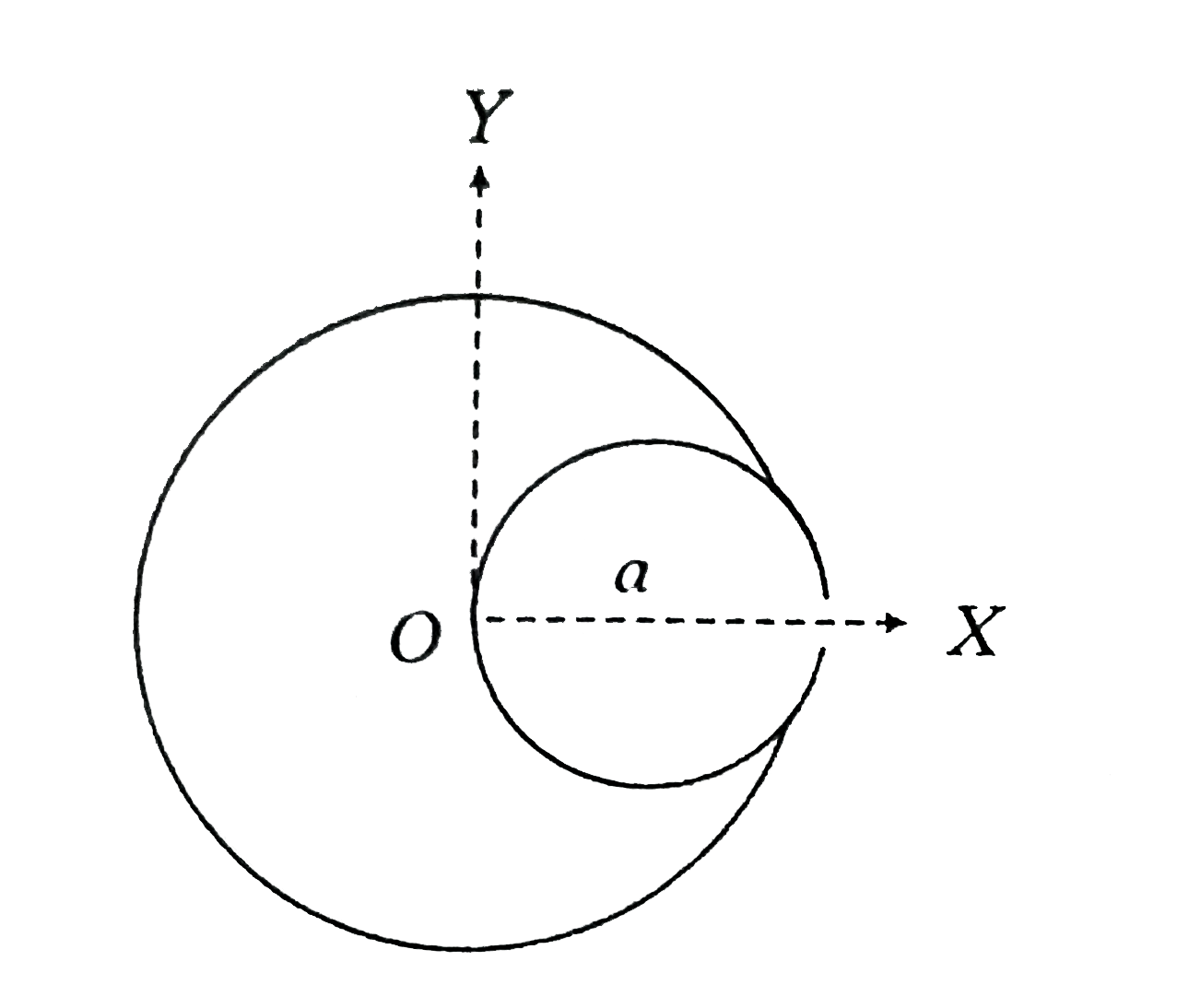 A(−a6,a)B(−a2,0)C(−a6,0)D(−a3,0)
A(−a6,a)B(−a2,0)C(−a6,0)D(−a3,0)Find moment of inertia of half disc of radius R2 and mass M about its centre. A smaller half disc of radius R1 is cut from this disc
 AM4(R21+R22)BM8(R21+R22)CM16(R21+R22)DM32(R21+R22)
AM4(R21+R22)BM8(R21+R22)CM16(R21+R22)DM32(R21+R22)
From a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
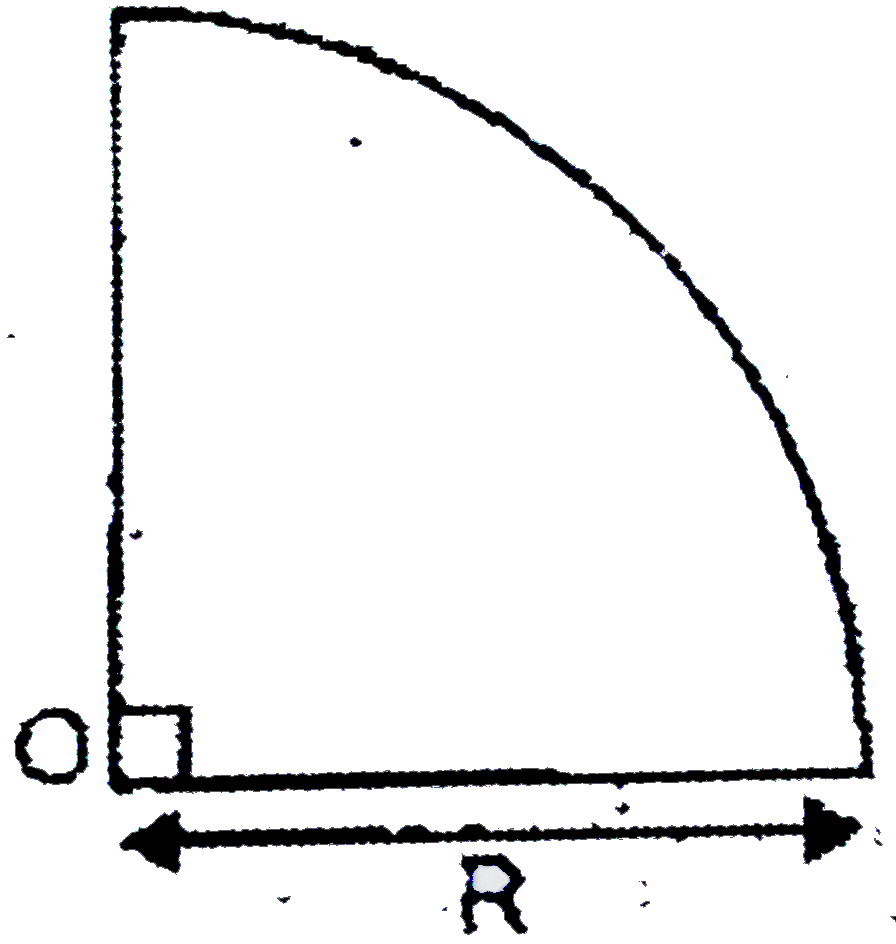
View SolutionThe radius of gyration of a uniform circular disc of radius R, about any diameter of the disc is
View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
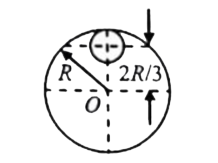
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference of the discs coincoid . The centre of mass of the new disc is αR from the centre of the bigger disc . the value of α is
View Solution

