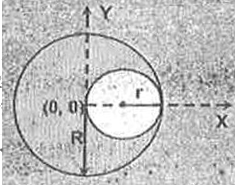
Figure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is $R / 2$ . Find the centre of mass of the remaining part of the disc.

Video Solution

Answer

Step by step video & image solution for Figure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R//2. Find the centre of mass of the remaining part of the disc. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Knowledge Check

A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
A $\frac{r}{5}$
B $\frac{r}{4}$
C $\frac{r}{2}$
D $\frac{r}{3}$
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A $\frac{3}{35} c m$
B $\frac{1}{35} c m$
C $\frac{3}{10} c m$
DNone of these
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A3/35 cm
B1/35 cm
C3/10 cm
D7/35 cm

PHYSICS GALAXY - ASHISH ARORA-LINEAR MOMENTUM & ITS CONSERVATION-exercise 1.3

Home
Ask Doubt
Profile

Figure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

Topper's Solved these Questions

Similar Questions

Knowledge Check

A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-

A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is

A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is

PHYSICS GALAXY - ASHISH ARORA-LINEAR MOMENTUM & ITS CONSERVATION-exercise 1.3

Figure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is $R / 2$ . Find the centre of mass of the remaining part of the disc.