Given a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
3MR2/32
5MR2/16
1MR2/64
none of these
The correct Answer is:C
Mass is cut disc m1=M4
Moment of inertia of original disc about axis 1:

I=14MR2
Moment of inertia of small disc about axis 1:
I'=14m1(R2)2+m1(R2)2
516m1R2=564MR2
Required moment of inertia
I−I'=14MR2−564MRS2=1164MR2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Multiple Correct
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Subjective
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionObtain an expression for moment of inertia of a uniform circular disc about a diameter of the disc.
View Solution
Knowledge Check
A small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
A0.4mB2.4cmC1.8cmD1.2cmA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
A0.4 cmB2.4 cmC1.8 cmD1.2 cmA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
Ar5Br4Cr2Dr3
A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
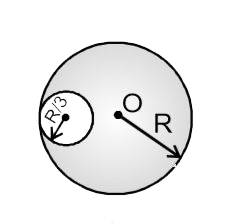
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe moment of inertia of a uniform semicircular disc of mass disc through the centre is
View Solution

