In a rectangle $A B C D, A B = 21$ and $B C = 1$ . Axes $\times$ and $y y$ pass through centre of the rectangle. The moment of inertia is least about :
.

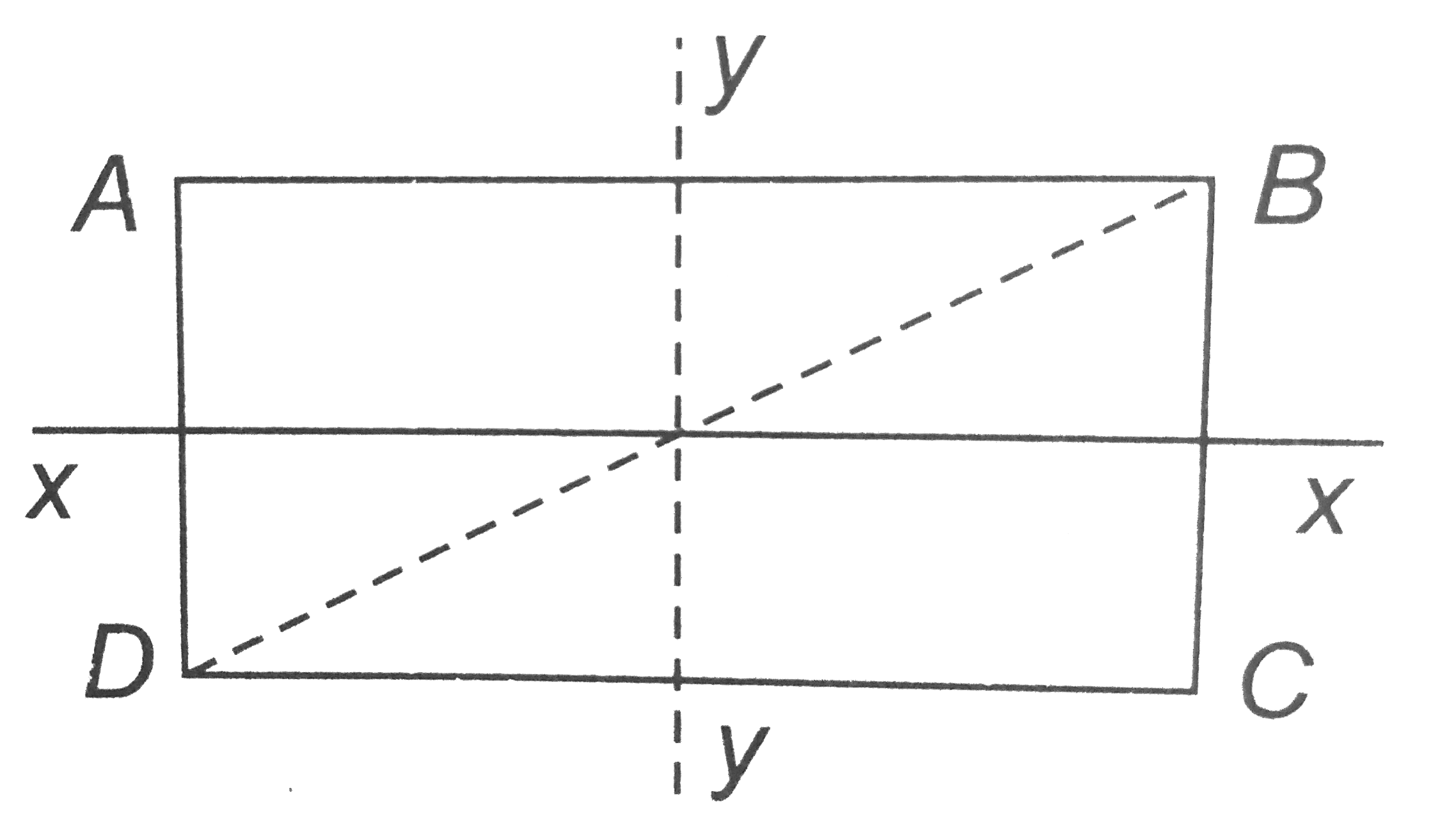$B C$

$B D$

$H F$

$E G$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

In a rectangle ABCD, AB= 15 cm $∠ B A C = 60^{\circ}$ then BC is equal to
A $15 \sqrt{3}$
B $\frac{15 \sqrt{3}}{2}$
C $\frac{15}{\sqrt{3}}$
D $\frac{15}{2 \sqrt{3}}$
In a rectangle ABCD , AB = 15 cm and $∠ B A C = 60^{\circ}$ , then the length of side BC is
A $15 \sqrt{2}$ cm
B15 cm
C $15 \sqrt{5}$ cm
D $15 \sqrt{3}$ cm
In a rectangle $A B C D (B C = 2 A B)$ . The moment of inertia is maximum along axis through

A $B C$
B $A B$
C $H F$
D $E G$