A small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
MR29
516MR2
916MR2
54MR2
The correct Answer is:C
Applying theorem of parallel axes.
I=MR22+M(R4)2,I=MR22+MR216,I+9MR216
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Multiple Correct
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Subjective
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
On the flat surface of a disc of radius aa small circular hole of radius b is made with its centre at a distance c from the centre of the disc. If mass of the whole un cut disc is M, calculate the moment of inertia of the holed disc about the axis of the circular hole.
[12[a2+2c2−b4a2]]
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View Solution
Knowledge Check
A circular disc of mass M and radius R is suspended from a nail in the wall. The nail is fixed very near to the rim of the disc. The moment of inertia of the disc about an axis along the nail is
AMR2BMR22C32MR2DMR24Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
AMR22BMR24CMR23DMR212The adjoining figure shows a disc of mass M and radius R lying in the X-Y plane with its centre on X - axis at a distance a from the origin. Then the moment of inertia of the disc about the X-axis is
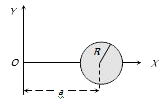 AM(R22)BM(R24)CM(R24+a2)DM(R22+a2)
AM(R22)BM(R24)CM(R24+a2)DM(R22+a2)
Moment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionA circular disc is of mass M and radius r. From it a circualr piece is cut out with a radius of the disc as its diameter. Find the moment of inertia of the remainder about the axix of the disc
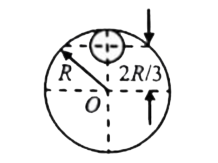
View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionThe moment of inertia of a uniform circular disc of mass M and radius R about any of its diameters is 14MR2. What is the moment of inertia of the disc about an axis passing through its centre and normal to the disc?
View Solution

